§ 3.6. Рефракция радиоволн в тропосфере. Эквивалентный радиус земного шара

Отличие коэффициента преломления тропосферы от единицы и изменение его с высотой существенно влияют на распространение радиоволн, особенно УКВ диапазона.

Траектория волны в сферической слоистой среде

Разобьем мысленно тропосферу на тонкие сферические слои, в пределах каждого из которых коэффициент преломления будем считать неизменным (рис. 3.7).

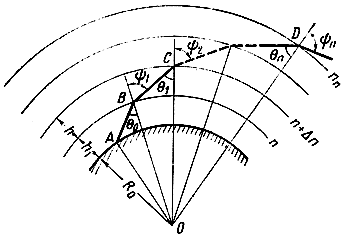
Рис. 3.7. Рефракция радиоволн в сферической слоистой тропосфере

Пусть из точки А излучается волна, падающая под углом θ₀ на границу раздела слоев в точке В. При переходе во второй слой происходит преломление волны, причем, если коэффициент преломления убывает с высотой, угол преломления ψ₁ оказывается больше угла падения θ₀. На границе раздела второго, третьего и всех следующих слоев также происходит преломление радиоволны. В результате этого волна движется по траектории, имеющей вид ломаной линии ABCD. Если толщину слоев уменьшить и перейти к плавному изменению коэффициента преломления, то ломаная ABCD в пределе будет стремиться к некоторой кривой. Таким образом, при прохождении волны в неоднородной среде ее траектория искривляется. Это явление носит название рефракции. При рассмотрении тропосферы как слоистой среды траекторию волны можно определить из треугольника ВОС, в котором

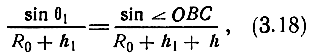
где на основании закона преломления

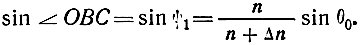
Преобразуя выражение (3.18), получим уравнение траектории волны в сферической слоистой тропосфере:

Чем больше величина Δn, тем больше угол θ₁ отличается от угла θ₀ и тем больше траектория отходит от прямолинейной.

Чтобы траектория была обращена выпуклостью вверх, коэффициент преломления должен убывать с высотой (Δn < 0).

Если пренебречь кривизной Земли и для простоты считать, что поверхности с одинаковым коэффициентом преломления являются плоскостями, параллельными поверхности Земли, то траекторию волны в такой среде можно определить из рис. 3.8. На границе раздела каждого из слоев тропосферы действует закон преломления:

или, поскольку ψ₁ = θ₁,

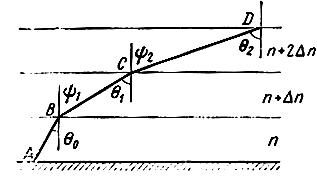
Рис. 3.8. Траектория волны в плоской слоистой среде

Таким образом, при распространении волны в плоской слоистой среде выполняется условие постоянства произведения коэффициента преломления волны на синус угла падения этой волны:

Определим радиус кривизны траектории волны, предположив, что поверхность Земли является плоскостью, а тропосфера - неоднородной средой.

На рис. 3.9 изображены две поверхности с постоянным коэффициентом преломления, отстоящие одна от другой по высоте на малый интервал dh, причем коэффициент преломления на расстоянии dh изменяется на величину dn. Волна, падающая на нижнюю поверхность под углом θ, преломляется и падает на верхнюю поверхность под углом θ + dθ. На участке аb траектория волны представляется отрезком кривой с радиусом кривизны ρ. Радиусы Oa и Ob являются нормалями к кривой в точках а и b. Угол между касательными к кривой в точках а и b равен dθ, следовательно, и угол aOb равен dθ.

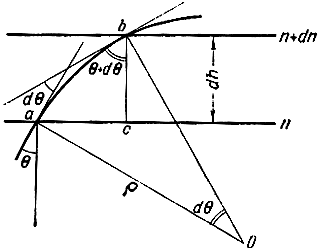
Рис. 3.9. К определению радиуса кривизны траектории волны в неоднородной тропосфере

Радиус кривизны траектории

Отрезок ab определяем из треугольника abc:

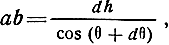
откуда

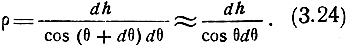
Взяв полный дифференциал уравнения траектории в плоской слоистой среде (3.22), выразим cosθ dθ через n и dn:

откуда

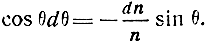
Подставляя это выражение в (3.24), получим

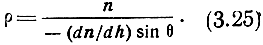
Поскольку основной интерес представляет распространение пологих лучей (θ → 90°) и n ≈ 1, выражение (3.25) можно переписать в виде

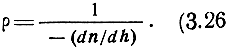
С учетом сферичности Земли и тропосферы в принятых приближениях радиус кривизны траектории волны выражается таким же образом.

В последней формуле знак "минус" показывает, что траектория имеет положительную кривизну, т. е. обращена выпуклостью вверх, когда коэффициент преломления n убывает с высотой (dn/dh < 0).

Если коэффициент преломления меняется с высотой по линейному закону (dn/dh = const), то радиус кривизны траектории не меняется с высотой и траектория представляет собой окружность.

Таким образом, влияние тропосферы на распространение радиоволн заключается в искривлении траектории волны.

Учет влияния тропосферной рефракции на распространение радиоволн

Изложенные в главе 2 методы расчета напряженности поля земных волн не учитывали влияния тропосферы и рассматривали прямолинейное распространение волны. Для упрощения расчетов при учете влияния тропосферы в некоторых случаях оказалось удобным свести распространение волны по криволинейной траектории к распространению волны по прямолинейной траектории. Такое упрощение производится путем введения понятия эквивалентного радиуса земного шара.

Картину распространения волн по криволинейной траектории вблизи реальной земной поверхности (рис. 3.10, а) заменяют картиной распространения волн по прямолинейной траектории вблизи поверхности Земли с измененным радиусом R_э (рис. 3.10, б).

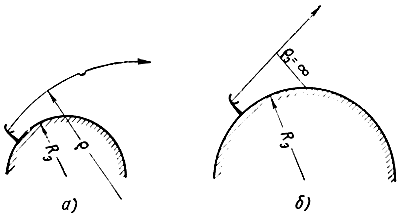
Рис. 3.10. Определение эквивалентного радиуса Земли

Понятием эквивалентного радиуса земного шара можно пользоваться в том случае, когда коэффициент преломления меняется с высотой по линейному закону.

Тогда уравнение траектории волны в сферической слоистой тропосфере (3.19) можно записать в виде

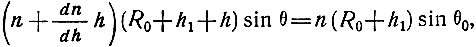
или

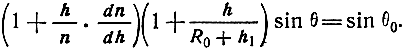
Раскрывая скобки и пренебрегая малым членом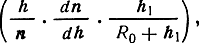  

а также учитывая, что n ≈ 1 и R₀ + h₁ ≈ + R₀, получаем

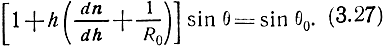
При распространении волны в эквивалентной однородной тропосфере углы падения волны на сферические слои равны соответствующим углам в реальной неоднородной тропосфере (θ₀, θ₁, ..., см. рис. 3.7), и уравнение траектории волны записывается в виде

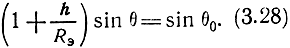
Сравнивая выражения (3.27) и (3.28), видим, что тропосферу можно рассматривать как однородную среду с неизменным по высоте значением коэффициента преломления, если вместо реального радиуса Земли ввести эквивалентный радиус, определяемый соотношением

откуда

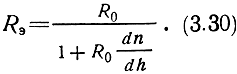
Выпрямленный луч проходит над эквивалентным земным шаром на той же высоте, что и криволинейный луч над реальной земной поверхностью.

Отношение эквивалентного радиуса Земли к реальному обозначают через k и определяют в соответствии с формулой (3.30):

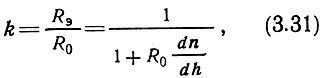
Если коэффициент преломления n меняется с высотой по линейному закону и

то такая рефракция называется нормальной тропосферной рефракцией.

Влияние тропосферной рефракции на распространение радиоволн необходимо учитывать при рассмотрении сравнительно протяженных трасс, на которых сказывается влияние кривизны земной поверхности.

Перечислим основные случаи применения эквивалентного радиуса Земли:

1. Определение расстояния прямой видимости с учетом рефракции. Без учета рефракции расстояние прямой видимости определяется формулой (2.2). Учесть влияние рефракции можно, заменив в выражении (2.2) величину R₀ на kR₀:

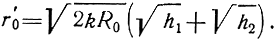
В условиях нормальной рефракции k = ⁴/₃ и

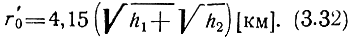
Следовательно,

т. е. при нормальной тропосферной рефракции расстояние прямой видимости возрастает на 15%.

2. Определение напряженности поля при использовании интерференционных формул с учетом сферичности Земли.

Приближенно влияние тропосферной рефракции на напряженность поля можно учесть при условии применимости формулы Введенского (2.29), подставляя в формулу приведенных высот (2.31) значение эквивалентного радиуса Земли:

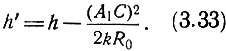
При нормальной рефракции h' > h, следовательно, напряженность поля возрастает.

3. Определение напряженности поля в зоне дифракции с учетом рефракции, что также приводит к увеличению напряженности поля в соответствии с формулами (2.65).

При изменении метеорологических условий происходит изменение величины dn/dh, вызывающее колебания напряженности поля. Помимо изменения силы сигнала, изменяются углы прихода радиоволн, что при узких диаграммах направленности может привести к ослаблению силы приема или перерыву связи.