§ 6.4. Определение напряженности электрического поля в месте приема и определение наименьших применимых частот

Методы расчета напряженности электрического поля на коротких волнах являются полуэмпирическими, поскольку в расчет входит ряд величин, полученных экспериментальным путем. Наиболее соответствующим физической картине распространения коротких волн является метод А. Н. Казанцева [11].

Волна, распространяясь в ионосфере, претерпевает поглощение в каждом из слоев. Это поглощение можно учесть, вводя экспоненциальный множитель в формулу для расчета напряженности электрического поля:

где Е_m′ - амплитуда напряженности электрического поля, рассчитанная без учета поглощения радиоволн в ионосфере; Г - суммарный коэффициент поглощения, учитывающий поглощение во всех слоях ионосферы.

Непоглощенная напряженность электрического поля определяется по формуле

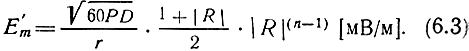
Здесь Р - мощность, излученная антенной, Вт; D - коэффициент направленного действия антенны; r - расстояние от точки передачи до точки приема по поверхности Земли, км; |R| - модуль коэффициента отражения от Земли; n - число отражений от ионосферы.

Множитель (1 + |R|) учитывает влияние земной поверхности вблизи антенны [см. выражение (2.16)], а множитель |R|^(n-1) - потери энергии при отражении от поверхности Земли в промежуточных точках.

Коэффициент 2 в знаменателе формулы (6.3) вводится для учета влияния постоянного магнитного поля Земли. Считают, что, во-первых, мощность, излученная антенной, делится поровну между обыкновенной и необыкновенной составляющими волны, но необыкновенная составляющая сильно поглощается и теряется для приема. Во-вторых, радиоволна, отраженная от ионосферы, имеет поляризацию, близкую к круговой, а для приема коротких волн применяются линейные антенны, поэтому принимается только половина мощности пришедшей волны. В результате принимаемая мощность уменьшается в 4 раза, а напряженность поля - в 2 раза.

Коэффициент поглощения в каждом слое ионосферы вычисляют как интеграл поглощения по всему пути, проходимому волной в данном слое. Например, при прохождении в слое D

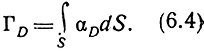
Согласно уравнению (4.27) коэффициент поглощения

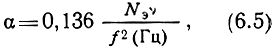
причем величины N_э и ν меняются с высотой и, следовательно, являются функциями пути S.

Для вычисления интеграла в выражении (6.4) задаются определенными зависимостями N_э и ν от высоты. Обычно считают, что N_э изменяется с высотой по параболическому закону, а ν - экспоненциально. В результате вычисления интеграла (6.4) для различных слоев А. Н. Казанцевым построены графики зависимости интегральных коэффициентов поглощения от рабочей частоты для данной критической частоты слоя. Зависимости оказываются различными при прохождении волны через слой и при отражении волны от слоя.

Графики интегральных коэффициентов поглощения радиоволны в слоях D, Е и F приведены на рис. 6.4.

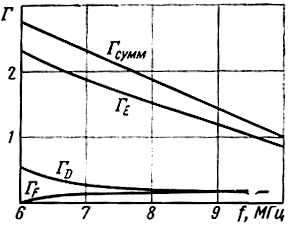
Рис. 6.4. Графики интегральных коэффициентов поглощения радиоволн в различных слоях ионосферы (лето, полдень, расстояние 1500 км)

В этом случае с повышением частоты коэффициент поглощения уменьшается, как и величина α [см. уравнение (6.5)]. С увеличением угла падения волны на слой поглощение увеличивается, что обусловлено увеличением пути, проходимого волной в слое, как изображено на рис. 6.5, а.

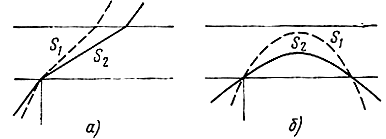
Рис. 6.5. Изменение длины пути волны в ионосферном слое с изменением частоты и угла падения: а - при прохождении волны; б - при отражении волны

Частотная зависимость поглощения для случая отражения волны от слоя F обратная: с увеличением рабочей частоты поглощение возрастает. Это объясняется тем, что более высокие частоты отражаются на большей высоте и путь S, проходимый волной внутри слоя, возрастает (рис. 6.5, б). Хотя значение а уменьшается с повышением частоты, увеличение пути приводит в этом случае к возрастанию интегрального коэффициента поглощения. При увеличении угла падения волны на слой путь сокращается, так как более пологие волны отражаются на меньшей высоте, и коэффициент поглощения уменьшается.

Таким образом, для расчета напряженности электрического поля коротких волн следует определить непоглощенную напряженность поля по формуле (6.3) и по графикам рис. 6.5 для данной рабочей частоты и критических частот слоев найти величину Г.

Для расчета НПЧ нужно знать амплитуду минимальной напряженности электрического поля Е_{m min}, необходимой для уверенного приема, которая определяется уровнем помех в месте приема. Тогда из выражения (6.2) можно определить максимально допустимый коэффициент поглощения:

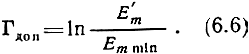
Из графиков рис. 6.4 определяют значение НПЧ на заданной величине Г_доп.

В "Инструкции по расчету коротковолновых линий радиосвязи" [59] подробно изложен метод расчета напряженности поля и НПЧ и приведен необходимый графический материал.

Нанося на одном и том же графике суточные изменения МПЧ и НПЧ, получают представление о диапазоне рабочих частот, который можно применять в разное время суток. Пример такого графика для радиотрассы Москва - Вашингтон приведен на рис. 6.6.

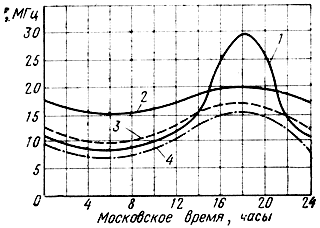
Рис. 6.6. Диапазон рабочих частот для радиотрассы Москва - Вашингтон (январь 1957 г.): 1 - МПЧ; 2 - НПЧ для мощности передатчика 1 кВт и приема на телефон; 3 - НПЧ для мощности передатчика 100 кВт и приема на телефон; 4 - НПЧ для мощности передатчика 100 кВт и приема на телеграф

Путем увеличения мощности передатчика можно снизить величину НПЧ. Для мощности передатчика 1 кВт и приема на телефон график НПЧ (кривая 2) почти все время проходит выше графика МПЧ (кривая 1), т. е. в этих условиях большую часть суток прохождение радиоволн невозможно. При увеличении мощности передатчика до 100 кВт НПЧ снижаются примерно на 4 МГц (кривая 3). Переход к телеграфному приему, требующему меньшего значения Е_{m min} снижает НПЧ еще на 1÷1,5 МГц. Приведенный пример показывает, что выбор рабочей частоты в (коротковолновом диапазоне является сложной, иногда неразрешимой задачей.