Глава четвертая. Физические основы работы электронных приборов типа М

4-1. Движение электронов в скрещенных однородных электрическом и магнитном полях

Стационарные поля в приборах типа М. В § 1-2 уже отмечалось, что приборами типа М называют электронные СВЧ приборы, в которых движение электронов происходит в скрещенных электрическом и магнитном полях. Иначе говоря, векторы напряженностей электрического и магнитного полей в таких приборах взаимно перпендикулярны. В случае плоской конструкции электродов (рис. 4-1, а) вектор ε напряженности электрического поля нормален к поверхностям электродов, а вектор В индукции магнитного поля лежит в плоскости, параллельной плоскостям электродов и перпендикулярен вектору ε.

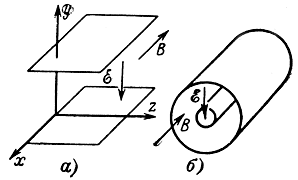
Рис. 4-1. Электрическое и магнитное поля в приборах с плоской (а) и цилиндрической (б) конструкцией электродов

В приборах с электродами цилиндрической конструкции (рис. 4-1, б) вектор ε направлен по радиусу к оси, а вектор В параллелен оси.

В таких скрещенных полях электроны подвергаются воздействию сил электрического и магнитного полей и движутся по сложным траекториям.

Сила, действующая на электрон в скрещенных полях, слагается в общем случае из силы действия электрического поля и силы магнитного поля

где

Вектор силы F_м нормален к плоскости, в которой расположены векторы - сомножители υ и В. Направление вектора F_м силы Лоренца легко найти, пользуясь правилом правой руки.

Для прямоугольной системы координат силу F_м можно записать в виде

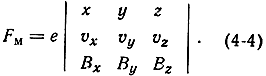
Раскрывая детерминант и учитывая, что F = ma, получим выражения для составляющих силы F_м по осям координат:

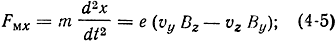
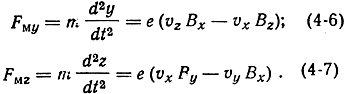
Для составляющих суммарной силы F_σ можно записать:

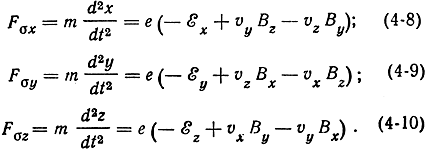
Случай плоских электродов. Рассмотрим частный случай движения электрона в суммарном поле, когда векторы ε и В взаимно перпендикулярны и электрическое поле образовано двумя плоскими параллельными электродами k и а (рис. 4-2), разность потенциалов которых U_a = εd, где d - расстояние между электродами.

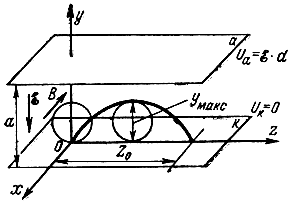
Рис. 4-2. Движение электрона во взаимно перпендикулярных однородных электрическом и магнитном полях

Пренебрежем краевым эффектом и будем считать поля однородными.

Для этого случая ε_x = 0; В_х = 0, ε_у = 0; В_у = -В; ε_z = - ε; B_z = 0.

Электрон находится в начале координат (x = y = z = 0), его начальная скорость υ₀ = 0 и уравнения (4-8) - (4-10) принимают вид:

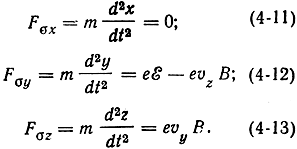
Движение электрона будет происходить в плоскости yoz. Перепишем уравнения (4-12) и (4-13) в виде

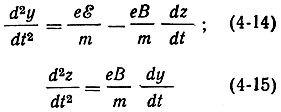
и обозначим:

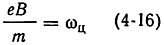
и

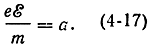
Тогда (4-14) и (4-15) можно переписать следующим образом:

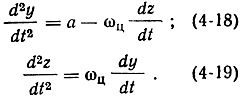
Проинтегрируем уравнение (4-19)

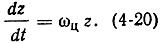
Постоянная интегрирования с = 0, так как при t = 0 x = z = 0, dy/dt = 0 и dz/dt = 0; подставляя (4-20) в (4-18), получим:

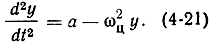
Решение этого уравнения дает

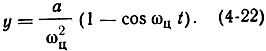
Подставляя (4-22) в (4-20) и интегрируя его, будем иметь:

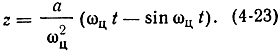
Полученные выражения являются параметрическими уравнениями циклоиды - траектории точки окружности, катящейся по оси z. Составляющие скорости движения электрона можно определить, продифференцировав по времени (4-22) и (4-23):

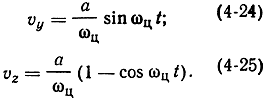
Отсюда видно, что движение электрона слагается из равномерного поступательного движения вдоль оси z с постоянной скоростью, равной а/ω_ц = ε/В, и кругового движения с частотой соц, называемой циклотронной частотой.

Наибольшее отклонение электрона вдоль оси у соответствует значению cos ω_цt = -1, т.е. ω_цt = π. При этом согласно (4-22), (4-16) и (4-17)

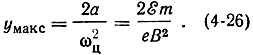
Отсюда легко определить радиус катящейся окружности

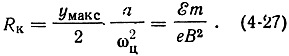
Траектория электрона пересечет ось z через время, равное полному обороту окружности, образующей циклоиду: ω_цt = 2π. Определяя отсюда время t = 2π/ω_ц подставляя его в (4-23), получим:

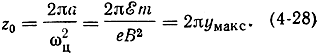
Когда электрон входит в рассмотренное выше суммарное поле с начальной скоростью υ₀ под некоторым углом а к оси z (рис. 4-3), уравнения (4-18) и (4-19) имеют такой же вид, но так как при t = 0, dz/dt = υ_0z и dy/dt = υ_0y, то интегрирование их приводит к иному результату:

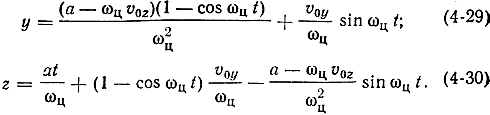
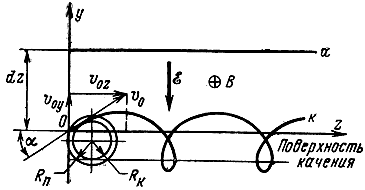
Рис. 4-3. Общий случай движения электрона во взаимно перпендикулярных однородных электрическом и магнитном полях (ε ⊥ B; υ₀ ≠ 0)

Эти выражения являются параметрическими уравнениями трохоиды. Полученные ранее параметрические уравнения циклоиды (4-22) и (4-23) являются частным случаем (4-29) и (4-30), когда υ₀ = 0.

Трохоидальное движение совершает точка на спице колеса, катящегося вдоль оси, причем радиус производящей окружности, точка которой описывает трохоиду, в общем случае не равен радиусу катящейся окружности. Эти радиусы равны лишь для циклоидального движения (υ₀ = 0).

Составляющие скорости электрона при трохоидальном движении можно определить, продифференцировав по времени (4-29) и (4-30):

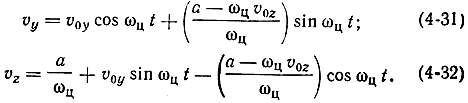
Отсюда видно, что движение вдоль оси z слагается из поступательного движения со скоростью а/соц, не зависящей от начальной скорости, и вращательного движения с циклотронной частотой соц, определяемой индукцией магнитного поля В. При υ_0y = υ_0z = 0 эти уравнения обращаются в (4-24) и (4-25).

Радиус производящей окружности можно определить, выделив из уравнений (4-29) и (4-30) члены, определяющие периодическое движение:

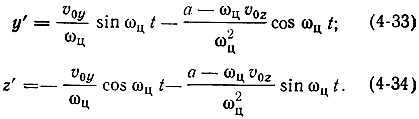
Отсюда видно, что радиус производящей окружности

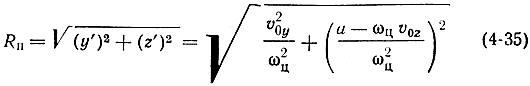
пропорционален квадрату начальной скорости электрона, т. е. его начальной энергии.

Для циклоидального движения (υ_0y = v_0z = 0)

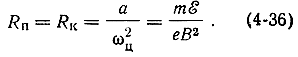
По трохоидальной траектории электрон может двигаться и тогда, когда энергия этектрона обладающего нулевой начальной скоростью, изменится в процессе его движения. При этом циклоида превратится в трохоиду. Если электрон при движении теряет энергию, то радиус производящей окружности уменьшается и электрон движется по укороченной циклоиде (рис. 4-4, а). При увеличении энергии электрона в процессе движения его траектория представляет собой удлиненную циклоиду (рис. 4-4, б).

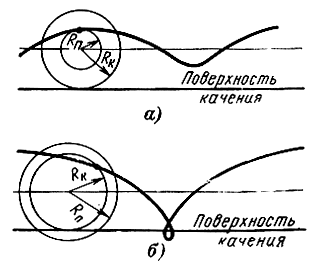
Рис. 4-4. Траектории движения электрона по укороченной (а) и удлиненной (б) циклоидам

Задача о движении электронов в скрещенных полях в приборах с цилиндрическими электродами может быть решена аналогично только что рассмотренной задаче. Уравнения для составляющих суммарной силы удобно при этом записать применительно к системе цилиндрических координат. Не повторяя еще раз всего рассмотрения, отметим лишь, что в системе с электродами цилиндрической конструкции движение электронов при υ₀ = 0 будет происходить по эпициклоидальной траектории (рис. 4-5).

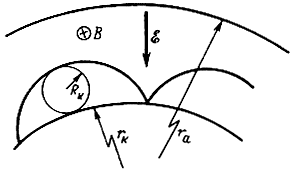
Рис. 4-5. Эпициклоидальная траектория движения электрона

Критический режим. Как следует из выражении (4-26) и (4-27), радиус R_k катящейся окружности и возвышение y_макс электрона над катодом (см. рис. 4-2) увеличиваются с ростом ε и обратно пропорциональны величине В². Следовательно если В = const и d = const, то с увеличением U_а должна возрастать и величина y_макс: наивысшая точка траектории электрона будет приближаться к электроду а. При некотором значении U_a величина y_макс будет равна d - расстоянию между электродами. Электрон коснется электрода а. Эта величина U_а называется критическим потенциалом: U_а = U_а.кр..

Из (4-26) легко получить выражение для критического потенциала

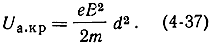
Для цилиндрических электродов это выражение имеет вид:

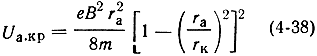
Зависимость U_a.кp = f(B) называется параболой критического режима (рис. 4-6).

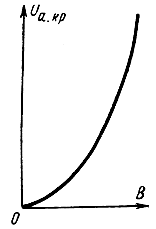
Рис. 4-6. Парабола критического режима

При U_а > U_а.кр электроны на первом витке циклоиды будут достигать электрода а. Такой режим называют докритическим и наоборот: при U_a < U_a.kp режим называют закритическим.

Траектории электронов для всех трех режимов в системах плоских и цилиндрических электродов показаны на рис. 4-7.

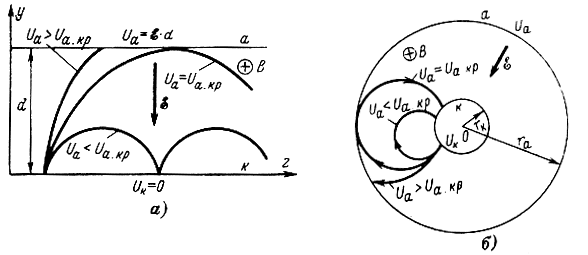
Рис. 4-7. Траектории движения электрона в плоском (а) и цилиндрическом (б) диодах, помещенных в магнитное поле, при различных значениях U_a

4-2. Взаимодействие электронов с неоднородным электрическим полем

Предположим, что система плоских электродов, рассмотренных в предыдущем параграфе, представляет собой некоторую замедляющую систему, в которой; существует бегущая электромагнитная волна. Постоянное электрическое поле создается за счет разности потенциалов U_a - U_k, а вектор магнитной индукции перпендикулярен плоскости чертежа.

Картину переменного электрического поля в такой системе можно представить с помощью силовых линий (рис. 4-8). Допустим, что между электродами системы, от ее начала к концу движется поток электронов. Рассмотрим взаимодействие электронов с неоднородным электрическим полем, для чего мысленно отметим три электрона, находящиеся в различных точках поля (рис. 4-9). Разложим векторы напряженности переменного электрического поля в этих точках на составляющие по осям у и z.

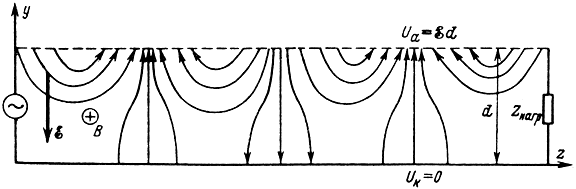
Рис. 4-8. Картина переменного электрического поля в замедляющей системе

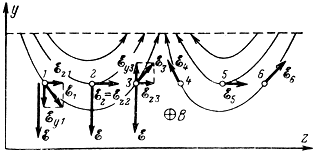
Рис. 4-9. Взаимодействие электронов с неоднородным электрическим полем (влияние поперечной составляющей поля)

Влияние поперечной составляющей поля. В точке 1 составляющая

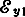
вектора напряженности переменного электрического поля совпадает по направлению с вектором ε постоянного поля. Суммарное поле в этой точке равно:

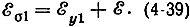
Следовательно, поступательная, вдоль оси z, скорость электрона в этой точке

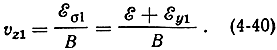
В точке 2 вектор

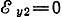
и, таким образом,

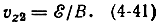
В точке 3 векторы ε и

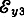
противоположны по направлению. Скорость электрона в этой точке вдоль оси z равна:

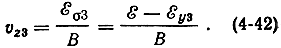
Таким образом, в точке 1 электрон за счет действия поперечной составляющей электрического поля получает дополнительное ускорение; в точке 2, в силу ε_y2 = 0, скорость электрона не меняется; в точке 3 ускорение отрицательно: электрон замедляет движение вдоль оси z. Если предположить, что начальная скорость электронов υ₀ при их вхождении в замедляющую систему равнялась фазовой скорости волны υ_ф, то при дальнейшем движении электронов с волной будет происходить их группирование в сгустки. Электрон 2 будет догонять электрон 1, а электрон 3 - оба электрона 1 и 2. Центром сгустка будет служить электрон 2, не изменивший своей скорости - невозмущенный электрон.

Если провести аналогичное рассмотрение для электронов 4, 5 и 6, находящихся в части поля с противоположной фазой, то нетрудно убедиться, что электрон 4 будет отставать от электрона 5, а электрон 6 - постепенно опережать его. Электрон в точке 5 будет служить центром области разрежения электронного потока.

Таким образом, под влиянием поперечной составляющей вектора напряженности переменного электрического поля электроны, движущиеся в скрещенных постоянных электрическом и магнитном полях, группируются в сгустки.

Влияние продольной составляющей поля. Рассмотрим влияние составляющей

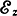
на примере двух электронов, служащих центрами сгустков и разрежения и находящихся, следовательно, в точках, соответствующих противоположным фазам поля (рис. 4-10). В точке 2 вектор

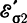
суммарной напряженности электрического поля отклоняется вправо от вектора ε постоянного электрического поля. Вектор

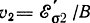
поступательной скорости электронов направлен под углом к оси z в сторону электрода с положительным потенциалом. Таким образом, электрон 2, а с ним и формирующийся в дальнейшем сгусток, будут по мере взаимодействия с переменным полем в процессе их совместного движения перемещаться по направлению к положительно заряженному электроду.

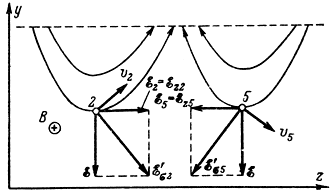
Рис. 4-10. Взаимодействие электронов с неоднородным электрическим полем (влияние продольной составляющей поля)

В точке 5 вектор υ₅ поступательной скорости электронов отклонен от оси z в противоположную сторону: к электроду с нулевым потенциалом. Следовательно, электроны, попавшие при вхождении в замедляющую систему в эту фазу поля и находящиеся впоследствии в области разрежения электронного потока, будут постепенно уходить на нижний электрод.

В дальнейшем при рассмотрении электронных приборов типа М мы убедимся, что электроны в сгустках, образующихся вблизи точки 2, являются рабочими электронами: они совершают полезную работу. При движении к положительному электроду уменьшается потенциальная энергия электронов в поле ε. Это изменение энергии вызвано взаимодействием электронов с переменным полем. Следовательно, потенциальная энергия электронов передается полю волны.

Электроны же, попавшие в область разрежения, - нерабочие электроны: они быстро удаляются из междуэлектродного пространства на нижний электрод.

Форма электронного пучка. Итак, под влиянием сил неоднородного электрического поля электроны в пучке меняют скорость движения: появляются переменные составляющие скорости как в продольном направлении (по оси z), так и в поперечном направлении (по оси у). В результате изменяется форма электронного пучка (рис. 4-11). Ленточный пучок электронов, сечение которого до взаимодействия с переменным полем очерчено пунктирными линиями, принимает волнообразную форму. В областях тормозящего поля (εz > 0) электроны не только группируются вокруг невозмущенногб электрона за счет изменения составляющей υ_z их скорости, но и смещаются в направлении к положительному электроду. Это последнее смещение тем больше, чем ближе электроны к поверхности замедляющей системы, т. е. чем интенсивней неоднородное поле. Электронный пучок деформируется: его границы в поперечном направлении расширяются.

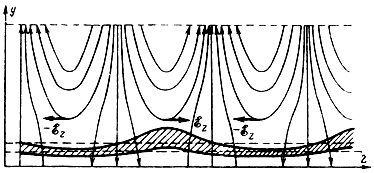
Рис. 4-11. Форма электронного пучка

Иная картина наблюдается в областях с ускоряющим полем (εz < 0). Здесь наряду с разгруппированием электронов по оси z происходит некоторое сужение пучка и отклонение его в сторону электрода с нулевым потенциалом.

Подробный анализ описанных явлений показывает [Л. 11], что получающаяся деформация пучка не сопровождается, как это было в приборах типа О, изменением объемной плотности заряда, т. е. модуляция по скорости не приводит к модуляции по плотности. В силу расширения границ пучка в областях образования сгустков и сужения пучка в разреженных областях объемная плотность заряда остается постоянной в любой точке. Меняется лишь поверхностная плотность заряда и его погонная плотность вдоль оси z. Однако при этом полный заряд естественно изменяется с координатой z: увеличивается в области расширения пучка и уменьшается там, где пучок сужается. Это сопровождается изменением поля пространственного заряда, которое вдоль координат y и z приобретает волновой характер.

Следует отметить также, что в результате различных по величине и знаку скоростей смещения электронов по осям у и z в разных частях поля возникают переменные составляющие токов в направлениях y и z, но при этом, как уже было сказано, объемная плотность заряда остается неизменной.

Возникновение поперечной составляющей поля пространственного заряда сопровождается некоторым изменением продольных скоростей электронов в зависимости от координаты y. Пучок как бы состоит из ряда слоев, скорости движения электронов в которых вдоль оси z различны.

Это явление, как мы увидим далее, расширяет область эффективного взаимодействия электронов с волной. Условия необходимого горячего синхронизма выполняются для более широкого спектра фазовых скоростей волны и, следовательно, в более широком диапазоне частот.

4-3. Энергетическое взаимодействие электронов с волной

Задача об энергетическом взаимодействии электронного потока с волной в приборах типа М несколько отличается от подобной задачи применительно к приборам О-типа. Это отличие объясняется различными механизмами обмена энергией между электронами и волной. В приборах типа О, как мы видели (§ 3-4), энергия волны пополняется при определенных условиях за счет кинетической энергии электронов, т. е. за счет их торможения продольной (z-й) составляющей электрического поля.

В приборах типа М электроны передают полю волны свою потенциальную энергию, смещаясь в поперечном относительно их движения (y-м) направлении. В предыдущем параграфе было показано, что в результате взаимодействия с волной электронный пучок деформируется: расширяется по оси у в областях группирования электронов и при дальнейшем движении смещается в этом же направлении к замедляющей системе. Оба эти процесса (расширение пучка и смещение его центра по оси y) вносят свой вклад в механизм передачи потенциальной энергии полю. В силу одновременного движения электронов по двум взаимно перпендикулярным направлениям (по осям y и z) задача об энергетическом взаимодействии становится двумерной. Выражение (3-11), записанное для мощности взаимодействия в комплексной форме, в этом случае принимает вид:

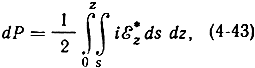
где ds - площадь поперечного сечения электронного пучка.

Подставляя в (4-43) выражения для тока i и поля ε_z и учитывая фазовые соотношения, можно, как и для приборов типа О, получить [Л. 11] зависимости активной Р_а и реактивной Р_r составляющих мощности взаимодействия от относительного угла пролета φ₀ (рис. 4-12).

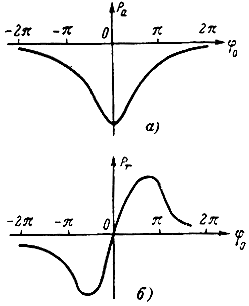
Рис. 4-12. Зависимость активной (а) и реактивной (б) составляющих мощности взаимодействия от величины относительного угла пролета

Из анализа приведенных кривых и их сравнения с подобными зависимостями для приборов типа О (рис. 3-5) можно сделать ряд важных выводов.

В отличие от приборов О-типа, где оптимальные условия передачи кинетической энергии электронов волне соответствуют относительному углу пролета φ ≈ -π (υ₀ > υ_ф0), в приборах со скрещенными полями максимум потенциальной энергии электронов волне передается при условии, что φ₀ = 0, т. е. в условиях холодного синхронизма (υ₀ = υ_ф0). Если это условие выполняется, то электроны движутся вдоль замедляющей системы по оси z с неизменной скоростью, равной скорости волны. Их кинетическая энергия не меняется. В процессе их смещения о оси у они теряют потенциальную энергию в электрическом поле прибора, которая и превращается в энергию волны.

Если же условия холодного синхронизма не выполняются (υ₀ ≠ υ_ф0), то, как идно из рис. 4-12, б, появляется реактивная составляющая Р_r мощности взаимодействия. Знак величины Р_r таков, что происходит "электронное" замедление волны, если υ₀ < υ_ф0, и наоборот, волна ускоряется в случае υ₀ > υ_ф0. В любом случае в процессе движения вдоль оси z система электронный пучок - волна будет стремиться к условиям горячего синхронизма, т. е. к условиям, при которых Р_r = 0 и электроны отдают волне наибольшую энергию. Степень такой самосинхронизации зависит от ряда причин в том числе и от величины объемного заряда. С его ростом компенсация холодного рассинхронизма увеличивается.