
2.8. Методы измерений физико-механических параметров материалов, используемых в конструкциях ГГ
В современных конструкциях ГГ используются различные материалы: целлюлоза, ткани, резины, пленки, различные виды металлической фольги и др., от выбора которых в значительной степени зависят параметры и качество звучания ГГ. Поэтому разработка техники измерений физико-механических параметров этих материалов имеет чрезвычайно большое значение для производства ГГ. Информация об этих параметрах необходима для выбора оптимальной совокупности материалов для каждого типа ГГ, разработки требований к направленному синтезу новых материалов, создания методов машинного расчета и проектирования ГГ (что невозможно без точных значений основных физико-механических параметров всех используемых материалов), контроля разбросов в процессе производства ГГ.
Как следует из классической теории упругости для идеально упругого твердого изотропного тела (у которого упругие свойства одинаковы по всем направлениям), связь между приложенными усилиями (напряжениями) σ и вызванными ими деформациями ε описывается законом Гука. Для одноосного растяжения - сжатия он имеет вид
σ(t) = Eε(t). (2.5)
Коэффициент пропорциональности называется модулем Юнга или модулем нормальной упругости, он характеризует жесткость материала. Отношение относительной деформации образца в поперечном направлении εx к его относительной упругой деформации в продольном направлении εy называется коэффициентом Пуассона μ = -εy/εx. Касательные напряжения τxy и соответствующие им упругие сдвиговые деформации связаны между собой через модуль сдвига: τ = Gγxy. В трехмерном случае связь между напряжениями и деформациями описывается обобщенным законом Гука:
εx = (1/E)|σx - μ(σy + σz)|; γxy = (1/G)τxy;
εy = (1/E)|σy - μ(σx + σz)|; γyz = (1/G)τyz;
εz = (1/E)|σz - μ(σx + σy)|; γxz = (1/G)τxz;
упругие постоянные Е, G, μ связаны между собой соотношением:
E = 2G(1 + μ). (2.6)
Таким образом, для описания упругих свойств изотропного тела достаточно измерить только две независимые константы: Е, μ или Е, G. Для анизотропных материалов, т. е. таких, у которых упругие свойства по разным направлениям различны, закон Гука может быть записан в тензорной форме
εik = Ciklmσlm,
где εik - компоненты тензора деформации, σlm - компоненты тензора напряжений, Ciklm - коэффициенты податливости. Для вычисления всех видов деформации в анизотропном теле необходимо знать 21 независимый коэффициент Ciklm. Связь этих коэффициентов с физически измеренными модулями упругостей следующая: C1111 = l/Ex; C2222 = l/Ey; С3333 = 1/Ez; C1212 = 1/Gxy и т. д. Если упругие свойства материала различаются только в двух взаимно перпендикулярных направлениях, то материал называется ортотропным и для описания его используется девять независимых постоянных. В том случае, если материал имеет толщину существенно меньшую других геометрических размеров, некоторыми напряжениями и деформациями можно пренебречь и число независимых коэффициентов сокращается до шести - для анизотропных материалов и до четырех - для ортотропных (называемый в таком случае - ортотропный слой). Большинство применяемых в ГГ материалов с известной степенью приближения могут быть отнесены к изотропным материалам или к материалам типа "ортотропного слоя". Поэтому для определения упругих свойств изотропных материалов в ГГ измеряется модуль Юнга (Е) и коэффициент Пуассона (μ) (иногда используется измерение модуля сдвига G). Для ортотропных материалов определяются модули упругости в направлениях 0 и 90° (т. е. взаимноперпендикулярных) и под углом 45°. В остальных направлениях в плоскости ортотропии модули вычисляются по формулам
Eφ = E0/(cos4φ + b0sin22φ + c0sin4φ);
c0 = E0/E90; b0 = E0/E45 - (c0 + 1)/4,
где Е0, E45, E90 - модули упругости, измеренные под углом 0, 45, 90°. Следует отметить, что в реальных материях идеально упругие деформации, т. е. такие, которые полностью и мгновенно исчезают после снятия нагрузки и их величина не зависит от скорости напряжения, реализуются только с известной степенью приближения (например, для металлов). В подавляющем большинстве используемых в ГГ материалов (целлюлозе, тканях, эластичных пленках и. др.) имеют место вязкоупругие деформации, при которых наблюдается запаздывание реакции системы на изменение внешнего поля, т. е. отставание деформации от создаваемого в материале напряжения. При периодическом процессе нагружений связь между напряжением и деформацией описывается гистерезисной кривой. Площадь петли определяется разностью между удельной работой, затраченной при нагружений, и работой, совершенной при разгрузке. Эта площадь характеризует величину энергии, которая осталась после деформации в образце, и рассеивается, переходя в тепловую, химическую и др. Если скорость нагружения очень мала ωн < ωниж, т. е. материал успевает придти в равновесное состояние, то площадь петли, а следовательно необратимые потери энергии в материале, малы. Аналогично при больших скоростях нагружения ωн > ωверх элементы структуры материала не успевают перегруппироваться, при этом деформации и потери невелики. В тех же случаях, когда время действия Тн напряжения соизмеримо с временем релаксации материала τрел (время релаксации материала τрел есть время перехода материала из неравновесного состояния в равновесное после снятия нагрузки под действием теплового движения молекул), потери максимальны. Для большинства применяемых в ГГ материалов эти частоты ωн попадают в звуковой диапазон, где Тн ≈ τрел. Уравнения классической теории не описывают вязкоупругого поведения материалов. В настоящее время достаточно хорошо разработана линейная теория вязкоупругости, в которой связь между напряжением и деформацией описывается линейными дифференциальными или интегральными уравнениями. Уравнение (2.5) в случае вязкоупругих деформаций преобразуется к виду
σ(t) = E*ε(t). (2.7)
При циклических нагружениях, когда напряжения и деформации изменяются по синусоидальному закону, модуль Юнга
E* = E′(ω) + jE″(ω),
где E′(ω) = ReE* = Eω2τ2/(1 + ω2τ2), (E′(ω) - называется динамическим модулем упругости); τ - время релаксации материала:
1/ωE″(ω) = η/1(1 + ω2τ2)
(1/ωE″(ω) - называется динамической вязкостью). Эти формулы получены для одной из моделей вязкоупругого поведения тела - модели Максвелла. Для других моделей формулы могут иметь иную форму. Из (2.8) следует, что сдвиг фаз между напряжением и деформацией может быть определен как tgφ = E″/E′. Угол φ называется углом потерь, он связан с величиной механической добротности QМ (определенной в данном случае как отношение колебательной энергии, запасенной за четверть периода, к энергии, рассеянной за период QM = 2πW3/Wpac) соотношением QM = l/tgφ (при достаточно малом φ). Так как добротность связана с декрементом свободных колебаний Δ соотношением Δ = π/QM, (см. § 2.3), то угол потерь φ может быть определен из измерения свободных затухающих колебаний образца материала. Кроме того, он может быть измерен при резонансных испытаниях образца (по ширине резонансной кривой):
tgφ = 1/QМ = Δ/π = Δf/f,
где Δf - ширина резонансной кривой на уровне 0,7. В технической литературе используется также величина коэффициента потерь γ.
Все полимерные материалы в зависимости от температуры могут находиться в различном физическом состоянии: стеклообразном, переходном, вязкоэластичном (вязкоупругом) и вязкотекучем. Зависимости Е′ и tgφ от частоты в разных температурных зонах Т° соответствующих этим состояниям, значительно различаются. У материалов, находящихся в стеклообразном состоянии, Е′ и tgφ мало зависят от температуры и частоты (при комнатной температуре в таком состоянии находится целлюлоза, однако введение пластификаторов может резко снизить ее температуру стеклования). Другие материалы (резина, пленки и т, д.) могут при комнатных температурах находиться в вязкоупругом или переходном состоянии, где частотная зависимость Е′ и tgφ выражены значительно сильнее. Поэтому для описания физико-механических параметров материалов, используемых в ГГ в режиме динамических нагрузок, необходима разработка методов измерений частотной зависимости динамического модуля упругости E(φ ) и тангенса угла потерь tgφ(φ), а также точных методов измерения плотности ρ и толщины h материалов.
В теории материаловедения используются, как правило, статические характеристики упругих свойств материалов: жесткость, прочность на разрыв, сдвиг, растяжение, изгиб и др., техника измерений которых и соответствующая аппаратура достаточно хорошо разработаны, а многие методы измерений стандартизованы [35]. Для измерения динамических характеристик материалов в звуковом диапазоне в отечественной практике проектирования ГГ отработано несколько методов и создана соответствующая аппаратура [36-38]. В области низких частот используется метод возбуждения и регистрации вынужденных резонансных изгибных колебаний консольно закрепленного образца.
На рис. 2.20 дана схема установки, работающей по принципу "колеблющегося язычка". Образец 1 консольно крепится к основанию 8, которое поддерживается и центрируется двумя шайбами 2 и 7. С несущей шайбой основание жестко соединено шпилькой 6, колеблющейся свободно (не касаясь стенок) в отверстии керна магнитной системы 5. При пропускании синусоидального тока через звуковую катушку 3 основание приходит в колебания, возбуждая при этом изгибные колебания зажатого образца. Резонансные колебания свободного конца образца регистрируются либо оптическим методом, либо визуально. В качестве образцов используются полоски материала с размерами: длина l = 25...50 мм, толщина h = 0,2...0,5 мм, ширина t = 18 мм, что определяет рабочий диапазон 40...200 Гц. Модуль Юнга
E = 48π2ρ(fn/h)2(l/mn)4,
где n = 1,2; m1l = 1,875; m2l = 4,694. Погрешность измерений ΔE/E = Δρ/ρ + 2Δh/h + 4Δl/l. Несмотря на достаточно большую погрешность (20%), из-за простоты методики измерений и конструкции установка широко используется в практике лабораторных измерений материалов ГГ.
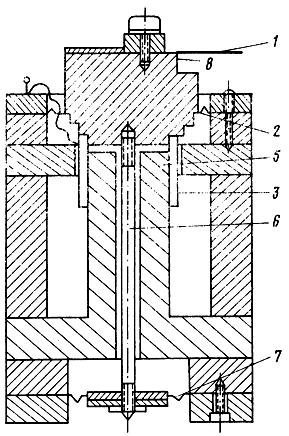
Рис. 2.20. Схема установки, работающей по принципу 'колеблющегося язычка'
На протяжении ряда лет в процессе разработок ГГ используется измерительная установка ИМУ-1, построенная по принципу "продольного маятника" [36]. Схема установки показана на рис. 2. 21. Образец 3 в виде полоски исследуемого материала закрепляется в вертикальном положении в жесткий зажим 1 на кронштейне, на другом конце образца крепится металлический груз 4. Продольные колебания в образце возбуждаются при воздействии на груз электромагнитного преобразователя 5. Колебания регистрируются пьезоэлементом (титанат бария) 8, который через электроизоляционную керамическую прокладку 7 приклеивается к кронштейну 6. Регистрирующий элемент помещен в электромагнитный экран 2. Электрическое напряжение на пьезоэлементе регистрируется микровольтметром. Частота возбуждения электромагнитного преобразователя сравнивается с частотой возбуждения образца на осциллографе по фигурам Лиссажу. Если масса груза М больше массы образца материала, то модуль Юнга
E = (2πfp)Ml/ht,
где fр - резонансная частота; l - длина образца, под которой понимается длина его свободного участка между зажимами заделки и груза; t - ширина образца; h - толщина.
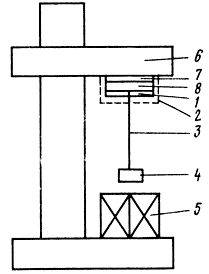
Рис. 2.21. Схема установки ИМУ-1, построенная по принципу 'продольного маятника'
При массе образца, соизмеримого с массой груза, вводится соответственная поправка. Коэффициент демпфирования γ также может определяться на этой установке по Ширине резонансной кривой. Длина образца может варьироваться от 20 до 150 мм, масса груза - от 1,5 до 300 г, резонансная частота при этом может изменяться в диапазоне 50...4000 Гц. Погрешность измерений модуля Юнга, зависящая от точности измерения толщины,
ΔE/E = Δl/l + Δh/h + Δt/t.
Измеренные на этой установке частотные зависимости модуля Юнга Е и коэффициента потерь γ в диапазоне 100...1000 Гц показаны на рис. 2.22. Как следует из результатов измерений, модуль Юнга Е имеет слабую частотную зависимость в этом диапазоне для непропитанной целлюлозы, а коэффициент γ изменяется существенно. Изложенные выше методики позволяют производить измерения в диапазоне частот до 2...3 кГц, при, этом могут использоваться только образцы из относительно жестких материалов (типа бумаги), так как к образцу прикладывается статическая нагрузка.
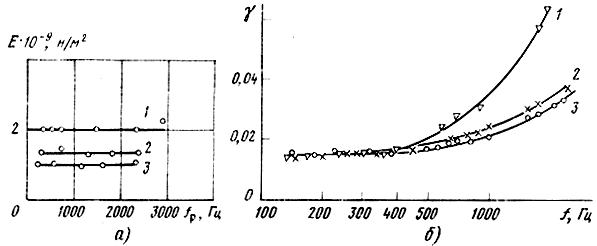
Рис. 2.22. Частотная зависимость модуля Юнга Е (а) и коэффициента затухания γ от частоты (б) для различных типов целлюлоз: 1 - СФА; 2 - 50% СФА; 50% СФИ; 3 - СФИ
Для расширения диапазона частот и возможности измерять вязкоупругие материалы (резина, ткани и др.) совместно с ИМП Латвийской АН СССР была создана установка (на базе прибора ИЧЗ-9) и отработана методика измерений [37]. Структурная схема установки показана на рис. 2.23. Образец 4 исследуемого материала, представляющий собой прямоугольную полоску, свернутую в цилиндр, с приклеенными к его торцам ферромагнитными пластинками устанавливается на измерительном стенда с помощью опор 3. Механические колебания образца возбуждаются электромагнитным преобразователем 7, соединенным с генератором 5 и частотомером 7. Второй электромагнитный преобразователь 2 преобразует механические колебания образца в электрические. Сигналы возбуждения сравниваются с колебаниями образца на осциллографе 6 по фигурам Лиссажу. Измерения проводятся на первой резонансной частоте. Для обеспечения измерений на других частотах меняются габаритные размеры образца и его масса. В образце возбуждаются продольные колебания и измеряются усредненные f01, f11, f21 (т. е. частоты, соответствующие резонансной частоте и границам полосы резонансной кривой на уровне 0,5 от амплитуды). По полученным значениям вычисляется фазовая скорость звука с в образце:
в области высоких частот m < M, где m - масса ферромагнитных пластинок, М - масса образца,
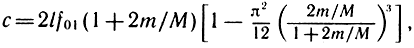
в области средних частот, m > М:
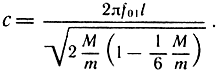
По полученным значениям с с помощью номограмм, построенным в [37], вычисляются коэффициент Пуассона и скорость продольных колебаний образца с0, по ней определяется модуль Юнга: E = ρс20. Таким методом можно измерять достаточно упругие материалы (бумагу, пленки и т. д.) на частотах до 16 кГц с погрешностью 10%. Мягкие материалы (резина, ткани и др.) измеряются на частотах свыше 1 кГц методом "составного образца". Трубчатый образец длиной l1, изготовленный из мягкого испытуемого материала, склеивается с трубчатым образцом длиной l2, изготовленным из уже исследованного материала, например бумаги. В составном образце также измеряется скорость продольного распространения и вычисляется Е. Максимальная погрешность измерений для резиноподобных материалов составляет 18%. Разработанная методика и установка на базе ИЧЗ-9 в настоящее время используется в практике разработок громкоговорителей для подбора материалов, анализа временной и температурной стабильности их физико-механических характеристик и т. д.
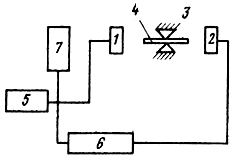
Рис. 2.23. Схема установки на базе прибора ИЧЗ-9
Большой статистический материал по измерению физико-механических параметров ГГ в производственных условиях был накоплен с помощью установки ДИПП-1 [38], работающий по принципу "крутильного маятника". Принципиальная схема установки показана на рис. 2.24. Образец исследуемого материала У в виде полоски закрепляется в стойку 2, к нижнему концу образца подвешивается с помощью зажима коромысло 3 и груз 4. Отклонением коромысла от положения равновесия возбуждаются в образце свободные крутильные колебания, измеряется время, в течение которого совершается несколько полных циклов колебаний. По результатам измерений определяется модуль сдвига G при разных значениях груза М: G = 12⋅JL/T2, где J - момент инерции коромысла, Т - период свободных колебаний, L - расстояние между зажимами образца. По этим данным строится зависимость G от α = Mb/4d3 в - ширина образца, d - толщина образца. На пересечении этой линии с осью абсцисс берется значение G0, т. е. модуль сдвига, приведенный к нулевой нагрузке. Значения модуля сдвига для некоторых материалов приведены в табл. 2.3.

Таблица 2.3
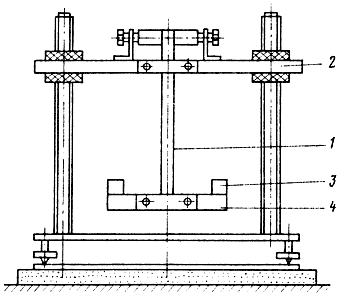
Рис. 2.24. Схема установки, работающей по принципу 'крутильного маятника'
Как следует из (2.6), измерения модуля сдвига G0 могут использоваться одновременно с измерением модуля Юнга для определения динамического коэффициента Пуассона μ. Если μ, известен, измерения Е или G0 эквивалентны. Рассмотренный метод дает возможность проводить измерения в области самых низких частот, дополняя измерения на продольных и изгибных колебаниях в более высокочастотной области.
В области высоких частот широкое распространение получили ультразвуковые импульсные методы определения физико-механических свойств материалов. Они основаны на измерении скорости распространения волн в исследуемом образце при его импульсном нагружении. По измерениям скоростей распространения упругих волн вдоль соответствующих осей упругой симметрии можно определить различные виды модулей Е и G. Ультразвуковые методы позволяют осуществлять непрерывный контроль технологических процессов, оценивать с большой точностью анизотропию материалов и т. д. Серийно выпускаются приборы; УК-10 ПМС, УК-13П, УК-22П, УК-16П, УК-19П, обеспечивающие цифровую индикацию результатов. Диапазон измерения времени распространения 20...1000 мс, рабочая частота 60...100 кГц. По сравнению с описанными выше установками для измерения в звуковом диапазоне частот методы и приборы для измерения с помощью ультразвуковых колебаний более оперативны, позволяют обеспечивать автоматизацию измерений, пригодны для широкого класса материалов. В технике разработок и производства ГГ они могут использоваться для материалов, у которых зависимость Е и γ от частоты выражена слабо, например металлическая фольга, некоторые пленки и т. д. Для материалов со значительной частотной зависимостью физико-механических параметров эти методы могут применяться с учетом поправок на характер этой зависимости.
Измерение толщины h и плотности ρ материалов, используемых в подвижных системах ГГ, является необходимым этапом при расчетах их динамических модулей, анализе производственных разбросов ГГ и применении различных методов расчета их элементов (диффузоров, подвесов и др.). Погрешность, с которой определяются h и ρ, оказывает очень существенное влияние на все последующие расчеты. Так, для расчета амплитуд смещения на поверхности диффузоров используется значение цилиндрической жесткости D = Eh3/[12(1 - μ2)], куда толщина h входит в виде h3. Для достаточно жестких материалов (фольги, кабельной бумаги и др.), толщина может измеряться обычным измерительным инструментом, например микрометром. Для мягких материалов такой метод дает большие погрешности, поэтому в тех случаях, когда требуется точное определение толщины материала, могут использоваться ультразвуковые методы измерения. Наиболее распространены эхоимпульсные толщиномеры, работающие по принципу измерения времени распространения t, с, ультразвукового импульса в изделии от поверхности ввода импульса по данной поверхности и обратно. При этом измеряемая толщина h = 1/2ct. Действие импульсных толщиномеров основано на измерении частоты повторения многократно отраженных импульсов, частоты или периода их свободных колебаний, или изменении амплитуды при сквозном прозвучивании. Минимальная толщина, измеряемая ультразвуковыми толщиномерами, составляет 0,1...0,3 мм при абсолютной погрешности измерений не более 1...5 мк. Серийно выпускаются толщиномеры УТ-91П, УТ-92П, УТ-ЗОПА, УТ-55БЭ.
При необходимости контроля более тонких изделий, например пленок, используемых в высокочастотных ГГ, можно применять приборы, основанные на анализе распространения радиоволн с информацией о толщине материала заложенной в амплитуде, фазе, смещении резонансной кривой, времени распространения импульса, положении максимума отраженной волны и т. д. В зависимости от метода анализа различают следующие типы радиоволновых толщиномеров: СТ-21Н, СТ-21НМ (амплитудно-фазовый метод) hиз = 1...20 мм; РРИ-73 (частотно-фазовый метод) hиз = 2 ± 15 мм; СИТ-1 (эллипсометрический метод) hиз = 0,01...0,025 мкм для металлических пленок; hиз = 1...100 мкм для диэлектрических пленок. Плотность материалов определяется обычным взвешиванием образца площади S: ρ = m/hS. При необходимости точного определения плотности может быть применен метод гидростатического взвешивания, когда образец взвешивается дважды: в воздухе m1 и в жидкости m2 заданной плотности ρж, тогда ρ определяется по формуле:
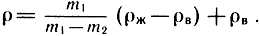

© RATELI.RU, 2010-2020
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
