§ 37. Закон полного тока

На рис. 80 показан проводник с током I, пронизывающий поверхность, ограниченную замкнутым контуром в виде окружности. Пусть центр окружности лежит на оси проводника. В пространстве, окружающем проводник с током, возникает магнитное поле. Так как отдельные точки контура находятся от проводника на равных расстояниях, то напряженность поля, созданная током в каждой точке контура, будет также одинаковой. Направление вектора напряженности поля H зависит от направления тока в проводнике и определяется по "правилу буравчика". Вектор H располагается по касательной к окружности контура.

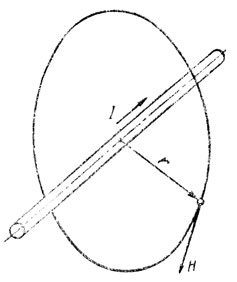
Рис. 80. К закону полного тока

Путем опытов и расчетов установлено, что произведение напряженности поля H в точках контура на длину этого контура l равно току I, пронизывающему поверхность, ограниченную данным контуром.

Таким образом,

В общем случае поверхность могут пронизывать несколько токов. Тогда определяют так называемый полный ток, т. е. находят алгебраическую сумму токов (∑I). Для этого случая можно записать:

Это выражение носит название закона полного тока. Закон полного тока является основным законом при расчете магнитных цепей и дает возможность в некоторых случаях легко определить напряженность поля.

Например, применив закон полного тока для определения напряженности магнитного поля в то на стоянии r от бесконечно длинного прямолинейного проводника с током (рис. 80), имеем следующее: полный ток равен току в проводнике ∑I = I; контур, проведенный на расстоянии r от проводника, совпадает с магнитной линией; длина контура l будет l = 2πr, поэтому H ⋅ 2πl = I, откуда H = ^I/_2πr.

Переходя к магнитной индукции, будем иметь B = μ_a^I/_2πr, т. е. мы получили то же выражение для магнитной индукции, которое было приведено выше Для такого же случая. Применим закон полного тока для определения напряженности поля по оси катушки, равномерно намотанной на кольцо (рис. 81). Контуром здесь является ось катушки (она же ось кольца). Площадь контура пронизывает полный ток, равный произведению тока I на число витков ω катушки, т. е. ∑I = Iω. Обозначив длину оси катушки через l, запишем закон полного тока:

откуда

или, переходя к магнитной индукции, будем иметь

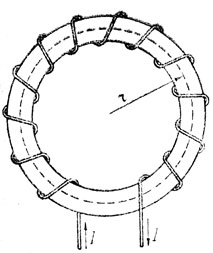
Рис. 81. К определению напряженности поля катушки, намотанной на кольцо

Если сечение кольцевой катушки обозначить S, то магнитный поток, проходящий внутри катушки, будет

Разрезав кольцо и выпрямив катушку, мы получим соленоид. Для соленоида бесконечно большой длины формулы для напряжённости поля H по оси соленоида, магнитной индукции В и магнитного потока Φ те же, что и для кольцевой катушки. Однако на практике, имея дело с соленоидами ограниченной длины, для определения H, В и Φ пользуются теми же формулами.