§ 55. Энергия электрического поля

Процесс заряда конденсатора заключается в разделении зарядов, т. е. создании на одной пластине избытка зарядов одного знака, а на другой пластине - другого знака.

Если соединить металлическим проводником пластины заряженного конденсатора, то противоположные по знаку электрические заряды, накопленные на пластинах, теперь воссоединяются. Наступает разряд конденсатора. Электрическое поле исчезает.

На рис. 115 схематически показан плоский заряженный конденсатор. Пусть расстояние между пластинами d будет мало и поэтому электрическое поле между пластинами будем считать однородным. Как нам известно, для однородного поля между напряжением и напряженностью поля существует следующая зависимость:

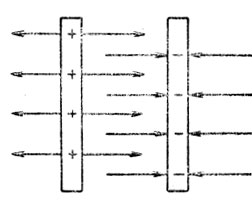
Рис. 115. Схема заряженного конденсатора

Учитывая, что для плоского конденсатора

получим

Отсюда следует, что если изменить расстояние между пластинами, то величина заряда пластин не изменится и напряженность поля также не изменится.

Напряженность электрического поля конденсатора ε можно рассматривать как сумму напряженностей ε₁ и ε₂ обусловленных зарядами двух заряженных пластин:

так как векторы напряженностей разноименно заряженных пластин в пространстве между ними имеют одно направление (рис. 116). Но ε₁ = ε₂, поэтому

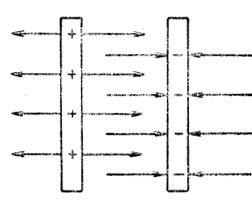
Рис. 116. Электрическое поле двух разноименно заряженных пластин

Разноименные заряды пластин взаимно притягиваются друг к другу. Сила взаимодействия зависит от величины заряда каждой из пластин и от величины напряженности поля. Так как при изменении расстояния между пластинами величина заряда пластин и величина напряженности поля остаются постоянными, то величина силы взаимодействия между пластинами тоже остается постоянной.

Сила, действующая на вторую пластину со стороны первой пластины,

будет равна силе, действующей на первую пластину со стороны второй пластины,

Таким образом,

Раздвигая пластины конденсатора от расстояния, равного нулю, до расстояния, равного d, будем совершать работу

идущую на преодоление силы взаимодействия между пластинами конденсатора.

Работа эта будет равна

Так как ε = ^U/_d,

то А = ¹/₂ qU.

Учитывая, что q = С ⋅ U, получим А = ^CU2/₂.

Механическая работа А, совершаемая при раздвижении пластин на основании закона сохранения энергии, должна быть равна количеству энергии W_э, запасенной в электрическом поле конденсатора, т. е.