§ 65. Цепь переменного тока с индуктивностью

Как мы видели выше, при включении, выключении и при всяком изменении тока в электрической цепи вследствие пересечения проводника своим же собственным магнитным полем в нем возникает индуктированная э.д.с. Эту э.д.с. мы называли э.д.с. самоиндукции. э.д.с. самоиндукции, как указывалось, имеет реактивный характер. Так, например, при увеличении тока в цепи э.д.с. самоиндукции будет направлена против э.д.с. источника напряжения и поэтому ток в электрической цепи не может установиться сразу. И наоборот, при уменьшении тока в цепи индуктируется э.д.с. самоиндукции такого направления, что, препятствуя убыванию тока, она поддерживает этот убывающий ток.

Как нам уже известно, э.д.с. самоиндукции зависит от скорости изменения тока в цепи и от индуктивности этой цепи (числа витков, наличия стальных сердечников):

В цепи переменного тока э.д.с. самоиндукции возникает и действует непрерывно, так как ток в цепи непрерывно изменяется.

На рис. 137 представлена схема цепи переменного тока, содержащей катушку с индуктивностью L без стального сердечника. Для простоты будем считать сначала, что активное сопротивление катушки r очень мало и им можно пренебречь.

Рис. 137. Цепь переменного тока, содержащая индуктивность

Рассмотрим внимательнее изменение переменного тока за время одного периода. На рис. 138 показана кривая изменения переменного тока. Первая половина периода разбита на мелкие одинаковые части.

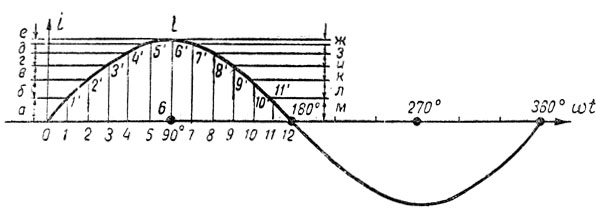
Рис. 138. Определение скорости изменения переменного тока

За промежуток времени 0-1 величина тока изменилась от нуля до 1-1'. Прирост величины тока за это время равен а.

За время, обозначенное отрезком 1-2, мгновенная величина тока выросла до 2-2', причем прирост величины тока равен б.

В течение времени, обозначенного отрезком 2-3, ток увеличивается до 3-3', прирост тока показывает отрезок в и т. д.

Так, с течением времени переменный ток возрастает до максимума (при 90°). Но, как видно из чертежа, прирост тока делается все меньше и меньше, пока, наконец, при максимальном значении тока этот прирост не станет равным нулю.

При дальнейшем изменении тока от максимума до нуля убыль величины тока становится все больше и больше, пока, наконец, около нулевого значения ток, изменяясь с наибольшей скоростью, не исчезнет, но тут же появляется вновь, протекая в обратном направлении.

Рассматривая изменение тока в течение периода, мы видим, что с наибольшей скоростью изменяется ток около своих нулевых значений. Около максимальных значений скорость изменения тока падает, а при максимальном значении тока прирост его равен нулю. Таким образом, переменный ток меняется не только по величине и направлению, но также и по скорости своего изменения.

Переменный ток, проходя по виткам катушки, создает переменное магнитное поле. Магнитные линии этого поля, пересекая витки своей же катушки, индуктируют в них э.д.с. самоиндукции.

На рис. 139 кривая i показывает изменение переменного тока в катушке. Как было уже указано, величина э.д.с. самоиндукции зависит от скорости изменения тока и от индуктивности катушки. Но так как индуктивность катушки в нашем случае остается без изменения, э.д.с. самоиндукции будет зависеть только от скорости изменения тока. Выше было показано, что наибольшая скорость изменения тока имеет место около нулевых значений тока. Следовательно, наибольшее значение э.д.с. самоиндукции имеет в те же моменты.

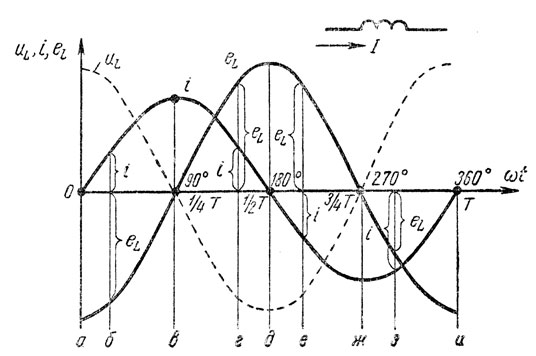
Рис. 139. Э.д.с. самоиндукции в катушке, включенной в цепь переменного тока

В момент а ток резко и быстро увеличивается от нуля, а поэтому, как следует из вышеприведенной формулы, э.д.с. самоиндукции (кривая e_L) имеет отрицательное максимальное значение. Так как ток увеличивается, то э.д.с. самоиндукции, по правилу Ленца, должна препятствовать изменению (здесь увеличению) тока. Поэтому э.д.с. самоиндукции при возрастании тока будет иметь направление, обратное току (положение б), что следует также из указанной формулы. Скорость изменения тока по мере приближения его к максимуму уменьшается. Поэтому э.д.с. самоиндукции также уменьшается, пока, наконец, при максимуме тока, когда изменения его будут равны нулю, она не станет равной нулю (положение в).

Переменный ток, достигнув максимума, начинает убывать. По правилу Ленца, э.д.с. самоиндукции препятствует току убывать и, направленная уже в сторону протекания тока, будет его поддерживать (положение г).

При дальнейшем изменении переменный ток быстро убывает до нуля. Резкое уменьшение тока в катушке повлечет за собой также быстрое уменьшение магнитного поля и в результате пересечения магнитными линиями витков катушки в них будет индуктироваться наибольшая э.д.с. самоиндукции (положение д).

Во вторую половину периода изменения тока картина повторяется и снова при возрастании тока э.д.с. самоиндукции будет препятствовать ему, имея направление, обратное току (положение е).

При убывании тока э.д.с. самоиндукции, имея направление, совпадающее с током, будет поддерживать его, не давая ему исчезнуть сразу (положение з).

На рисунке видно, что э.д.с. самоиндукции отстает по фазе от тока на 90°, или на 1/4 периода. Так как магнитный поток совпадает по фазе с током, то можно сказать, что э.д.с., наводимая магнитным потоком, отстает от него по фазе на 90°, или на 1/4 периода.

Нам уже известно, что две синусоиды, сдвинутые одна относительно другой на 90°, можно изобразить векторами, расположенными под углом 90° (рис. 140).

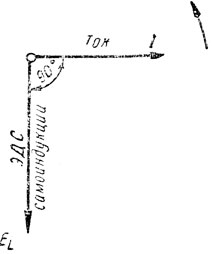
Рис. 140. Ток в катушке опережает э.д.с. самоиндукции по фазе на 90°

Так как э.д.с. самоиндукции в цепях переменного тока непрерывно противодействует изменениям тока, то, чтобы ток мог протекать по виткам катушки, напряжение сети должно уравновешивать э.д.с. самоиндукции. Иными словами, напряжение сети в каждый момент времени должно быть равно и противоположно э.д.с. самоиндукции.

Вектор напряжения сети, равный и противоположный э.д.с. самоиндукции Е_L, мы обозначим через U (рис. 141). Только при условии, что к зажимам катушки приложено напряжение сети, равное и противоположное э.д.с. самоиндукции, и, стало быть, это напряжение сети U уравновешивает э.д.с. самоиндукции Е_L, по катушке может проходить переменный ток I. Но в этом случае напряжение сети U будет опережать по фазе ток I на 90°.

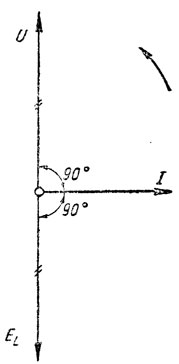
Рис. 141. Приложенное к катушке напряжение сети опережает ток на 90° и противоположно э.д.с. самоиндукции

Следовательно, в цепи с индуктивностью ток I отстает от приложенного напряжения U по фазе на 1/4 периода. На векторной диаграмме этому сдвигу фаз между напряжением U и током I соответствует угол α = 90° или ^π/₂.

Таким образом, в цепях переменного тока э.д.с. самоиндукции, возникая и действуя непрерывно, вызывает сдвиг фаз между током и напряжением. Возвращаясь к рис. 139, мы видим, что ток i по катушке будет проходить и тогда, когда напряжение сети (кривая u_L) равно нулю (положение в), и даже тогда, когда напряжение сети направлено в сторону, обратную току (положение г и з).

Итак отметим, что в цепи переменного тока, когда э.д.с. самоиндукции отсутствует, напряжение сети и ток совпадают по фазе. Индуктивная же нагрузка в цепях переменного тока (обмотки электродвигателей и генераторов, обмотки трансформаторов, индуктивные катушки) всегда вызывает сдвиг фаз между током и напряжением.

Можно показать, что скорость изменения синусоидального тока пропорциональна угловой частоте ω. Следовательно, действующее значение э.д.с. самоиндукции E_L может быть найдено по формуле

Как было отмечено выше, напряжение, приложенное к зажимам цепи, содержащей индуктивность, должно быть по величине равно э.д.с. самоиндукции:

Поэтому

Обозначая

Формула закона Ома для цепи переменного тока, содержащей индуктивность, имеет вид

Величина x_L называется индуктивным сопротивлением цепи, или реактивным сопротивлением индуктивности, и измеряется в омах. Таким образом, индуктивное сопротивление представляет собой своеобразное препятствие, которое цепь с индуктивностью оказывает изменениям тока в ней. Оно равно произведению индуктивности на угловую частоту:

Так как индуктивное сопротивление проводника зависит от частоты переменного тока, то сопротивление катушки, включаемой в цепь токов различной частоты, будет различным. Например, если имеется катушка с индуктивностью 0,05 гн, то в цепи тока частотой 50 гц ее индуктивное сопротивление будет

а в цепи тока частотой 400 гц

Та часть напряжения сети, которая преодолевает (уравновешивает) э.д.с. самоиндукции, называется индуктивным падением напряжения (или реактивной слагающей напряжения):

Рассмотрим теперь, какая мощность потребляется от источника переменного напряжения, если к зажимам его подключена индуктивность.

На рис. 142 даны кривые мгновенных значений напряжения, тока и мощности для этого случая. Мгновенное значение мощности равно произведению мгновенных значений напряжения и тока:

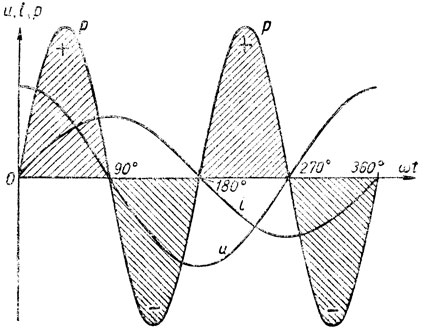
Рис. 142. Кривые мгновенных значений напряжения тока и мощности для цепи, содержащей индуктивность

Из чертежа видно, что если u и i имеют одинаковые знаки, то кривая р располагается выше оси ωt. Если же u и i имеют разные знаки, то кривая р располагается ниже оси ωt.

В первую четверть периода ток, а вместе с ним и магнитный поток катушки увеличиваются. Катушка потребляет из сети мощность. Площадь, заключенная между кривой р и осью ωt, есть работа (энергия) электрического тока. В первую четверть периода энергия, потребляемая из сети, идет на создание магнитного поля вокруг витков катушки (мощность положительная). Количество энергии, запасаемое в магнитном поле за время увеличения тока, можно определить по формуле

Во вторую четверть периода ток убывает. э.д.с. самоиндукции, которая в первую четверть периода стремилась препятствовать возрастанию тока, теперь, когда ток начинает уменьшаться, будет препятствовать ему уменьшаться. Сама катушка становится как бы генератором электрической энергии. Она возвращает в сеть энергию, запасенную в ее магнитном поле. Мощность отрицательна, и на рис. 142 кривая р располагается ниже оси ωt.

Во вторую половину периода явление повторяется. Таким образом, между источником переменного напряжения и катушкой, содержащей индуктивность, происходит обмен мощностью. В течение первой и третьей четвертей периода мощность поглощается катушкой, в течение второй и четвертой четвертей мощность возвращается источнику.

В этом случае в среднем расхода энергии не будет, несмотря на то что на зажимах цепи есть напряжение U и в цепи протекает ток I. Следовательно, средняя, или активная, мощность цепи, носящей чисто индуктивный характер, равна нулю.

Из графика, изображенного на рис. 142, видно, что мгновенная мощность цепи с индуктивностью два раза в течение каждого периода (когда ωt = 45°, 135° и т. д.) достигает максимального значения, равного ^U_м/_√2 ⋅ ^I_м/_√2 = UI. Этой величиной принято характеризовать количественно процесс обмена энергией между источником и магнитным полем. Ее называют реактивной мощностью и обозначают буквой Q.

Учитывая, что в рассматриваемой цепи U = I ⋅ x_L, получаем следующее выражение для реактивной мощности: