
§ 1.32. Расчет разветвленных цепей с взаимной индукцией
Для цепей с взаимной индукцией не все методы расчета электрических цепей пригодны. Возможен расчет по законам Кирхгофа, методам контурных токов и наложения.
Методом эквивалентного источника можно пользоваться только, когда ветвь с искомым током (напряжением) не имеет магнитной связи с другими ветвями схемы. Нельзя применять метод узловых потенциалов в обычном виде, а также преобразования источников э. д. с. в источники тока (и наоборот), и преобразования сопротивлений индуктивно связанных ветвей. При наличии в схеме источника тока его ток рассматривают как известный контурный ток.
При расчете в уравнениях, составленных по второму закону Кирхгофа, к напряжению на индуктивном элементе 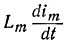 необходимо прибавить напряжение взаимной индукции
необходимо прибавить напряжение взаимной индукции 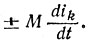 При гармоническом токе в случае применения комплексного метода учитывают комплексное напряжение взаимной индукции
При гармоническом токе в случае применения комплексного метода учитывают комплексное напряжение взаимной индукции 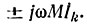 При этом напряжение взаимной индукции имеет знак плюс, если направление обхода индуктивного элемента и выбранное положительное направление тока в индуктивно связанном элементе совпадают относительно одноименных зажимов этих элементов.
При этом напряжение взаимной индукции имеет знак плюс, если направление обхода индуктивного элемента и выбранное положительное направление тока в индуктивно связанном элементе совпадают относительно одноименных зажимов этих элементов.
Пример. Для схемы рис. 1.14 составить уравнение по методу контурных токов. Считать, что ток источника тока 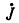 протекает по ветви R1, L1.
протекает по ветви R1, L1.
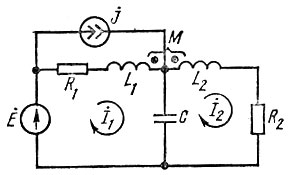
Рис. 1.14
Решение. Пусть направления обхода контуров совпадают с выбранным направлением контурных токов. При этом направление обхода индуктивного элемента L1(L2) и направление контурного тока I·1(I·2) не совпадают относительно одноименных зажимов. Поэтому напряжения взаимной индукции войдут в соответствующие уравнения со знаком минус (-jωМI·2, -jωMI·1). Ток источника тока 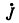 , протекая по индуктивному элементу L1, создает напряжение взаимной индукции на элементе L1 со знаком плюс (jωM
, протекая по индуктивному элементу L1, создает напряжение взаимной индукции на элементе L1 со знаком плюс (jωM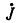 ), так как направления обхода L2 и тока в L1 одинаковы относительно их одноименных зажимов.
), так как направления обхода L2 и тока в L1 одинаковы относительно их одноименных зажимов.
Уравнения для контурных токов имеют вид:
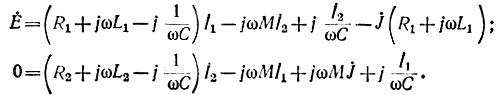

© RATELI.RU, 2010-2020
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
