
§ 2.4. Расчет цепей при периодических негармонических токах
Определение тока в линейных цепях при периодическом негармоническом источнике энергии осуществляют методом наложения. Напряжение источника э. д. с. u(t), заданное аналитически и удовлетворяющее условиям Дирихле, раскладывают в ряд Фурье. Частота каждой гармоники кратна частоте периодического негармонического напряжения kω при k = 0, 1, 2, 3 .... Отдельно для каждой гармоники напряжения рассчитывают соответствующую гармонику тока, применяя комплексный метод. При этом определяют комплексное сопротивление для каждой гармоники. Реактивное индуктивное сопротивление увеличивается пропорционально номеру гармоники: XLk - kωL. Реактивное емкостное сопротивление уменьшается с увеличением номера гармоники: XCk = 1/kωС. При изменении частоты kω активное сопротивление R полагают постоянным, пренебрегая поверхностным эффектом. После расчета всех гармонических составляющих тока записывают выражение для мгновенных значений тока:
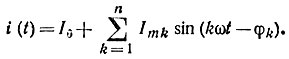
Алгоритм расчета. 1. Заданное аналитическое выражение для напряжения источника э. д. с. раскладывают в ряд Фурье: 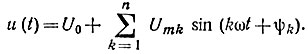 2. Каждую гармонику напряжения записывают в комплексной форме:
2. Каждую гармонику напряжения записывают в комплексной форме: 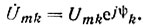 3. Комплексное сопротивление схемы определяют для каждой гармоники
3. Комплексное сопротивление схемы определяют для каждой гармоники 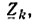 имея в виду что
имея в виду что 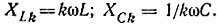 4. Для каждой гармоники напряжения
4. Для каждой гармоники напряжения 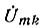 по комплексному сопротивлению находят комплексную амплитуду тока
по комплексному сопротивлению находят комплексную амплитуду тока 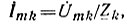 после чего записывают выражение мгновенного значения тока гармоники: ik = Imk sin (kωt - φk). 5. Мгновенное значение негармонического тока получают, суммируя мгновенные значения всех гармонических составляющих токов:
после чего записывают выражение мгновенного значения тока гармоники: ik = Imk sin (kωt - φk). 5. Мгновенное значение негармонического тока получают, суммируя мгновенные значения всех гармонических составляющих токов: 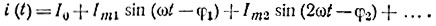

© RATELI.RU, 2010-2020
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
