§ 8.5. Составление характеристического уравнения

Первый способ. Определитель матрицы контурных сопротивлений (узловых проводимостей), составленный по методу контурных токов (узловых потенциалов) для переменного тока с заменой jω на р, приравнивают к нулю:

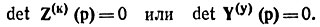
Данное алгебраическое уравнение решают относительно p, что позволяет получить корни характеристического уравнения p₁p₂ ... p_k ... .

Для схемы рис. 8.1 матрица контурных сопротивлений

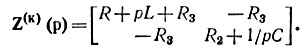
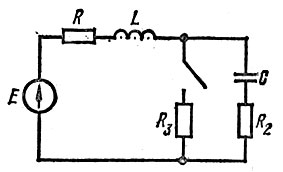
Рис. 8.1

Приравнивая к нулю определитель этой матрицы, получим характеристическое уравнение

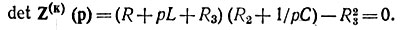
Второй способ. Входное комплексное сопротивление (проводимость) послекоммутационной схемы приравнивают к нулю и заменяют jω на p: Z_вх(р) = 0 или Y_вх(p) = 0.

Полученное алгебраическое уравнение решают относительно корней p_k.

В общем случае входное сопротивление (проводимость) находят по отношению к зажимам, к которым подключена ветвь с искомой переходной функцией (i_t, u_t). Для схемы рис. 8.2 входное сопротивление

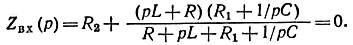
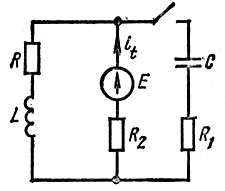
Рис. 8.2

Решая это уравнение относительно p, получим два корня p₁ и p₂.