§ 8.23. Алгоритм расчета переходных процессов методом интеграла Дюамеля

1. Классическим (операторным) методом находят переходную проводимость g(t) [переходную функцию напряжения y(t)], если искомым является ток (напряжение).

2. Вычисляют производную подынтегральной функции интеграла Дюамеля. Для этого сначала определяют производную по времени t, а затем t заменяют переменной интегрирования τ.

3. Записывают интеграл Дюамеля (в форме наиболее рациональной для решаемой задачи) с момента времени t = 0 до фиксированного момента времени. При этом учитывают возможные скачки тока (напряжения) в начале (t_k-) и конце (t_k+) каждого интервала до фиксированного момента времени t, вызываемые наличием скачков приложенного напряжения:

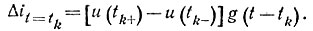
Пример. Найти выражение для напряжения u_C(t) в схеме рис. 8.9, а при подключении ее к напряжению (рис. 8.9, б).

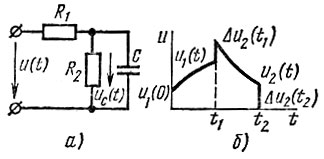
Рис. 8.9

Решение. Воспользуемся третьей (наиболее рациональной в данном случае) формой записи интеграла Дюамеля:

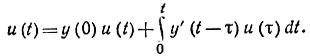
Определим переходную функцию напряжения (напряжение на емкостном элементе при включении схемы к постоянному напряжению, равному 1 В):

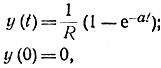
где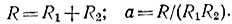

Найдем производную переходной функции на интервале времени t - τ:

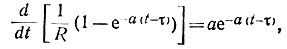
где τ - переменная интегрирования.

Запишем интеграл Дюамеля для трех интервалов времени.