
§ 9.15. Длинная линия с переменными по длине параметрами
Для длинной линии с переменными по длине параметрами справедливы дифференциальные уравнения второго порядка с переменными коэффициентами, зависящими от х. При гармонических напряжении и токе уравнения записывают для их комплексных значений. Например, при отсчете длины х от начала линии
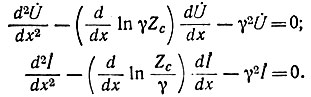
Примером линии с переменными по длине параметрами может служить экспоненциальная длинная линия без потерь, емкость которой увеличивается по экспоненциальному закону C = C0ekx (рис. 9.5). В этом случае при постоянной скорости распространения 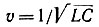 индуктивность уменьшается экспоненциально: L = L0e-kx, коэффициент распространения остается постоянным
индуктивность уменьшается экспоненциально: L = L0e-kx, коэффициент распространения остается постоянным 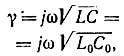 волновое сопротивление изменяется экспоненциально
волновое сопротивление изменяется экспоненциально 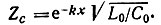
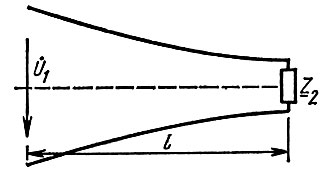
Рис. 9.5
Уравнения для экспоненциальной линии имеют постоянные коэффициенты:
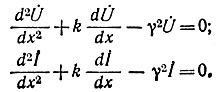

© RATELI.RU, 2010-2020
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
