Глава 11. Синтез линейных электрических цепей

§ 11.1. Общие сведения

Задача синтеза электрических цепей состоит в определении схемы и параметров всех ее элементов по заданному входному воздействию и требуемой выходной (входной) реакции. Другими словами, необходимо построить схему четырехполюсника по заданной передаточной функции (отношению выходной реакции к входному воздействию) или схему двухполюсника по входному сопротивлению (входной проводимости).

Синтез проводят по частотным либо по временным характеристикам цепи.

В качестве временной характеристики принимают реакцию цепи на воздействие импульсов прямоугольной формы.

В настоящее время отсутствует общий метод синтеза электрических цепей. Существует много частных методов синтеза, требующих индивидуального подхода к каждой конкретной задаче. Имеющиеся методы, накладывают ограничение на структуру синтезируемой схемы, характер и величину элементов, составляющих схему.

Рассмотрим простые методы синтеза двухполюсников, такие как разложение входного сопротивления 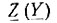на простые дроби и представление его в виде цепной (непрерывной) дроби (методы Фостера и Кауэра). Изложение синтеза четырехполюсников охватывает только вопросы построения схемы мостовой структуры в виде перекрытого Т-образного моста и реализации цепной схемы методом смещения нулей.

Входное воздействие произвольной формы обычно раскладывают на сумму гармонических составляющих спектральным методом (ряд Фурье, интеграл Фурье). Поэтому свойства пассивной электрической цепи могут быть определены по частотным зависимостям, например, входного сопротивления 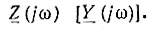В общем случае рассматривают эти зависимости в операторной форме как функцию комплексной частоты jω = р. Функции 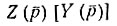характеризуются особыми точками на комплексной плоскости-нулями (корни уравнения 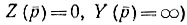и полюсами (корни уравнения 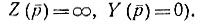Расположение особых точек на комплексной плоскости определяет входные функции с точностью до постоянного множителя. Функции 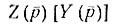могут быть физически реализованы, если они обладают определенными свойствами.

Синтез состоит из двух этапов:

1) аппроксимации заданных частотных (временных) характеристик в виде функций, удобных для реализации. Аппроксимирующие функции должны удовлетворять необходимым и достаточным условиям для построения схемы;

2) реализации найденной физически осуществимой функции путем определения элементов схемы и их параметров и построения самой схемы.

Решения задачи синтеза может не существовать, а если существует, то оно может оказаться не единственным.