§ 13.7. Расчет магнитной цепи при постоянном токе. Обратная задача

По заданным значениям F = Iω, размерам магнитопровода l_k, S_k и кривым намагничивания B_k(H_k) определяют магнитные потоки в магнитопроводе.

Неразветвленная магнитная цепь. Решение обратной задачи сводится к многократному решению прямой задачи расчета магнитных цепей постоянного тока. При этом задаются значением магнитного потока Φ', после чего находят м. д. с. F'. Если полученное значение F' не совпадает с заданным, то выбирают другие значения Φ", Φ"' и определяют соответствующие им F", F'". По вспомогательной характеристике Φ = f(F) и заданному значению F находят поток Φ.

Значение потока Φ' устанавливают по магнитному напряжению на участке с наибольшим магнитным сопротивлением (например, на воздушном зазоре), пренебрегая магнитными сопротивлениями других участков: Φ' = Iω/R_m.

Разветвленная магнитная цепь. В общем случае такую цепь рассчитывают графически по аналогии с расчетом нелинейных электрических цепей постоянного тока с двумя узлами.

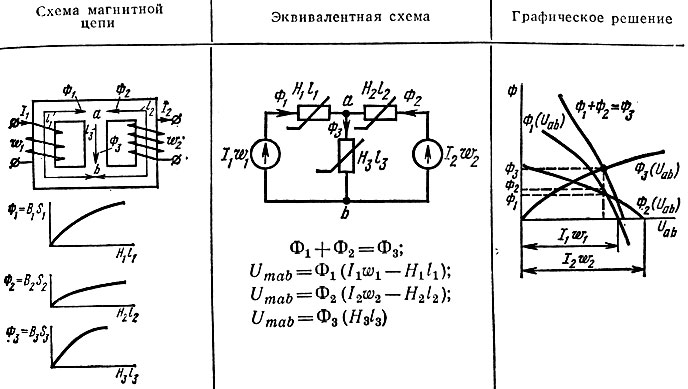
Сначала задаются положительным направлением магнитных потоков в стержнях магнитопровода. Затем составляют эквивалентную схему, на которой указывают направление м. д. с. и потоков, после чего по эквивалентной схеме составляют уравнения для магнитной цепи.

Уравнения решают графически в следующем порядке:

1) кривые намагничивания ферромагнитного материала каждого участка B_k(H_k) перестраивают в виде Φ_k = B_kS_k = f(H_kl_k);

2) с помощью характеристик Φ_k(H_kl_k) строят зависимое и Φ_k(U_mab), где U_mab - магнитное напряжение между узлами ab;

3) согласно первому закону Кирхгофа, складывают соответствующие ординаты характеристик, получая кривую Φ(U_mab);

4) проводя прямую, параллельную оси, на которой отложены потоки Φ_k, через точку пересечения кривой Φ(U_mab) и кривой, полученной по закону 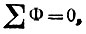определяют неизвестные потоки во всех стержнях магнитопровода.

Расчет магнитной цепи при постоянном токе