§ 18.8. Критерий устойчивости Гурвица

Критерий устойчивости Гурвица позволяет судить об устойчивости системы по коэффициентам характеристического уравнения без его решения. В системах, описываемых уравнениями первого и второго порядка, режим будет устойчивым, если коэффициенты характеристического уравнения положительные. Для систем, описываемых уравнениями третьего и выше порядка, это условие необходимо, но недостаточно.

Определитель Гурвица. Такой определитель составляют, исходя из характеристического уравнения

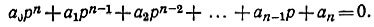
По диагонали определителя выписывают коэффициенты в соответствии с возрастающими степенями p, начиная с a₁. В столбцах выше диагонали располагают коэффициенты с возрастающими индексами по отношению к индексам диагональных коэффициентов. В столбцах ниже диагонали размещают коэффициенты с убывающими индексами. Для устойчивости линейной системы n-го порядка необходимо, чтобы все диагональные миноры определителя Гурвица были больше нуля.

Критерий устойчивости Гурвица

Пример. Исследовать на устойчивость эквивалентную схему (рис. 18.4) питания электрической дуги постоянным напряжением (R - добавочное сопротивление; L₀ - паразитная индуктивность). В. а. х. дуги дана на рис. 18.5, где точки А и В - точки устойчивого равновесия. Определить, какая из этих точек является точкой устойчивого равновесия.

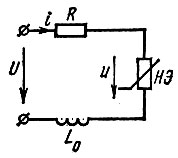
Рис. 18.4

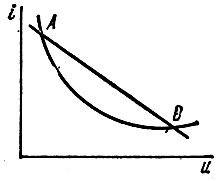
Рис. 18.5

Решение. Уравнение состояния равновесия согласно второму закону Кирхгофа имеет вид

Запишем уравнение состояния равновесия при i = I₀ = const:

Дадим приращение переменной Δi. Тогда

Разложим u(i) в ряд по степеням Δi, пренебрегая высшими степенями:

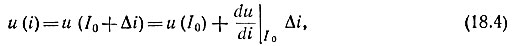
где 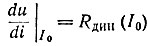- динамическое сопротивление. Учитывая R_дин, получим

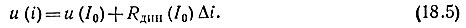
Подставим в выражение (18.1) уравнения (18.3)-(18.5):

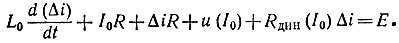
С учетом (18.2) найдем

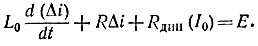
Из характеристического уравнения 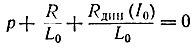определим

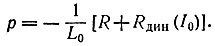
Корень уравнения вещественный отрицательный. Следовательно, для устойчивого равновесия должно удовлетворяться условие

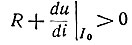
(критерий Кауфмана).

Этому условию удовлетворяет точка А на рис. 18.5.