§ 1. Как устроены атомы? Атом водорода

Из курса физики вы знаете, что атом любого вещества состоит из ядра и обращающихся вокруг него электронов. Такую модель атома предложил выдающийся английский физик Э. Резерфорд. Основываясь на этой модели, один из основоположников квантовой механики датский физик Н. Бор в 1913 году произвел первые правильные расчеты атома водорода, достаточно хорошо совпавшие с экспериментальными данными. Теория атома водорода, предложенная Бором, сыграла чрезвычайно важную роль в развитии квантовой механики, хотя в дальнейшем и претерпела существенные изменения.

Атом водорода. Постулаты Бора. Согласно модели Резерфорда-Бора атом водорода состоит из однократно заряженного положительного ядра и одного электрона, обращающегося вокруг него. В первом приближении можно предположить, что движение электрона происходит по траектории, представляющей собой окружность, в центре которой находится неподвижное ядро. В соответствии с требованиями классической электродинамики всякое ускоренное движение заряженного тела (в том числе и электрона) должно сопровождаться испусканием электромагнитных волн. В рассматриваемой модели атома электрон движется с колоссальным центростремительным ускорением, и поэтому он должен был бы непрерывно испускать свет. При этом энергия его должна была бы уменьшаться, а сам электрон должен был бы все ближе и ближе смещаться к ядру. Закончилось бы это тем, что электрон объединился бы с ядром ("упал" бы на ядро). Однако ничего подобного не происходит и атомы в невозбужденном состоянии не испускают света. Для объяснения этого факта Бор предложил два основных постулата.

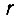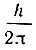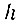Согласно первому постулату Бора электрон может находиться только на таких орбитах, для которых момент количества движения электрона (то есть произведение количества движения электрона mν на радиус орбиты ) кратен значению (где - постоянная Планка)^*. Пока электрон находится на одной из таких орбит, излучения энергии не происходит. Каждой разрешенной орбите электрона соответствует определенная энергия, или определенное энергетическое состояние атома, называемое стационарным. Находясь в стационарном состоянии, атом не излучает света. Математически первый постулат Бора можно записать так:

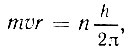
где 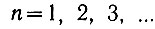- некоторое целое число, называемое главным квантовым числом.

^* (Постоянная Планка является универсальной физической константой и имеет смысл произведения энергии на время, называемого в механике действием. Благодаря тому что величина h представляется как бы элементарным количеством действия, постоянная Планка называется квантом (порцией) действия. Введение в физику понятия кванта действия было началом создания важнейшей физической теории XX века - квантовой теории. Квант действия очень мал: )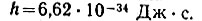

Второй постулат Бора содержит утверждение, что поглощение или испускание света атомом происходит только при переходах атома из одного стационарного состояния в другое. При этом энергия поглощается или испускается определенными порциями, квантами, значение которых hν определяется разностью энергий, соответствующих начальному и конечному стационарным состояниям атома:

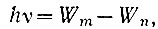
где 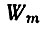- энергия начального состояния атома, 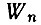- энергия его конечного состояния, ν - частота света, испущенного или поглощенного атомом. Если 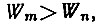то энергия излучается атомом, если же 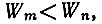то поглощается.

Позже кванты света получили название фотонов.

Таким образом, по теории Бора электрон в атоме не может изменять свою траекторию постепенно (непрерывно), а может лишь "перепрыгивать" с одной стационарной орбиты на другую. При переходе со стационарной орбиты, более удаленной от ядра, на стационарную орбиту, расположенную ближе к ядру, как раз и происходит испускание света.

Радиусы орбит и энергетические уровни атомов. Радиусы разрешенных электронных орбит можно найти, используя закон Кулона, соотношения классической механики и первый постулат Бора. Их значения определяются выражением

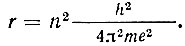
Самой близкой к ядру разрешенной орбите соответствует n = 1. Используя полученные экспериментально значения величин m, e и A, находим для ее радиуса значение

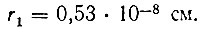
Эта величина как раз и принимается за радиус атома водорода. Любая другая орбита с квантовым числом n имеет радиус

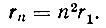
Таким образом, радиусы последовательно расположенных электронных орбит возрастают как квадрат числа n (рис. 1).

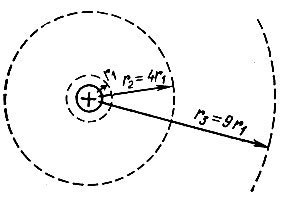
Рис. 1

Значение полной энергии атома, соответствующей нахождению электрона на n-ой орбите, определяется формулой

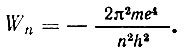
Эти значения энергий называются энергетическими уровнями атома, Если по вертикальной оси откладывать возможные значения энергии атома, то можно получить так называемый энергетический спектр разрешенных состояний атома (рис. 2).

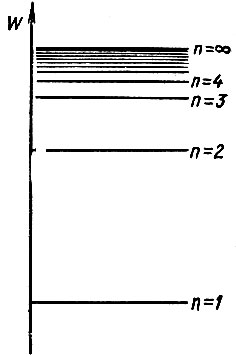
Рис. 2

Расстояние между последовательно расположенными энергетическими уровнями быстро уменьшается. Это можно легко объяснить: увеличение энергии атома (за счет поглощения атомом энергии извне) сопровождается переходом электрона на все более удаленные орбиты, где взаимодействие между ядром и электроном становится более слабым. По этой причине переход между соседними удаленными орбитами связан с очень малым изменением энергии. Энергетические уровни при этом располагаются настолько близко, что спектр становится практически непрерывным. В верхней части непрерывный спектр заканчивается уровнем ионизации атома (n = ∞), соответствующим полному отделению электрона от ядра (электрон становится свободным).

Знак "-" в выражении для полной энергии атома указывает на то, что энергия атома тем меньше, чем ближе к ядру находится электрон. Для того чтобы удалить электрон от ядра, необходимо затратить определенную энергию, то есть сообщить атому некоторую энергию извне. Энергия атома принимается равной нулю при n = ∞, т. е. в случае, когда атом ионизирован. Именно поэтому значениям 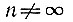соответствуют отрицательные значения энергии. Уровню с n = 1 соответствуют минимальная энергия атома и минимальный радиус разрешенной орбиты электрона. Этот уровень называется основным или невозбужденным. Уровни с n = 2, 3, 4, ... называются уровнями возбуждения.

Квантовые числа. В теории Бора предполагалось, что электронные орбиты имеют вид окружностей. Эта теория дала достаточно хорошие результаты только при рассмотрении самого простого атома - атома водорода. Но уже при расчете атома гелия она не смогла дать количественно правильные результаты. Определенным шагом вперед была планетарная модель атома, предполагавшая движение электронов подобно планетам солнечной системы по эллиптическим орбитам, в одном из фокусов которых располагалось ядро. Однако и эта модель быстро исчерпала себя, не дав ответа на многие вопросы.

Это связано с принципиальной невозможностью определения характера движения электрона в атоме. В доступном нашему наблюдению макромире нет аналогов этого движения. Мы не можем не только проследить путь движения электрона, но и даже определить точно его местонахождение в какой-либо определенный момент времени. Само понятие орбиты, или траектории движения электрона в атоме, лишено физического смысла. Никакой определенной последовательности появления электрона в различных точках пространства установить нельзя, он оказывается как бы "размазанным" в некоторой области, называемой обычно электронным облаком. Облако это, например, для невозбужденного атома водорода имеет форму шара, но плотность его не одинакова. Вероятность обнаружения электрона будет наибольшей вблизи сферы с радиусом r₁, соответствующим радиусу первой боровской орбиты. В дальнейшем под орбитой электрона в атоме мы будем понимать геометрическое место точек, которые характеризуются наибольшей вероятностью обнаружения электрона, или, другими словами, область пространства с наибольшей плотностью электронного облака.

Всегда сферическим электронное облако будет лишь для случая невозбужденного состояния атома водорода, когда главное квантовое число n = 1 (рис. 3, а). Если же n = 2, то, помимо сферического облака, размеры которого будут теперь в четыре раза больше, электрон может создать облако в виде своеобразной гантельки (рис. 3, б). С появлением несферичности области преимущественной локализации электрона (электронного облака) связано введение второго квантового числа l, называемого орбитальным квантовым числом. Каждому значению главного квантового числа n соответствуют положительные целочисленные значения квантового числа l от нуля до (n - 1):

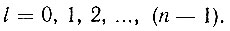
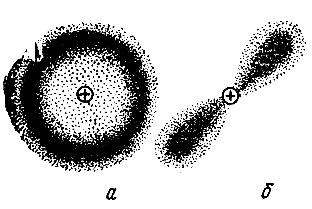
Рис. 3

Так, если n = 1, то l имеет единственное значение, равное нулю. Если же n = 3, то l может принимать значения 0, 1, 2. При n = 1 имеется только сферическая орбита, поэтому и l = 0. Когда n = 2, возможны как сферическая, так и гантелеобразные орбиты, поэтому и l может быть равным либо нулю, либо единице.

Если n = 3, то l = 0, 1, 2. Электронное облако, соответствующее значению l = 2, приобретает уже довольно сложный характер. Для нас, однако, важна не форма электронного облака, а то, какая ему соответствует энергия атома.

Энергия атома водорода определяется только значением главного квантового числа n и не зависит от значения орбитального числа l. Иначе говоря, если n = 3, то атом будет иметь определенную энергию W₃ независимо от того, на какой из возможных орбит, соответствующих данному значению n и различным возможным значениям l, находится электрон. Это означает, что при возвращении с уровня возбуждения на основной уровень атом будет испускать фотоны, энергия которых не зависит от значения l.

Рассматривая пространственную модель атома, необходимо иметь в виду, что электронные облака в нем имеют строго определенную ориентацию. Положение электронного облака в пространстве относительно выбранного каким-либо образом направления задается магнитным квантовым числом m, которое может принимать целочисленные значения от -l до +l, включая 0. При данной форме (данном значении l) электронное облако может иметь несколько различных ориентаций в пространстве. При l = 1 их будет три, соответствующих значениям магнитного квантового числа т, равным -1, 0 и +1. Если l = 2, то различных ориентаций электронного облака будет 5, соответствующих значениям m = -2, -1, 0, +1 и +2. Естественно, что если уж форма электронного облака в свободном атоме водорода не влияет на энергию атома, то тем более не влияет на энергию атома ориентация этого облака в пространстве.

Наконец, при более детальном рассмотрении экспериментальных данных выяснилось, что сами электроны могут находиться на орбитах в двух возможных состояниях, определяемых направлением так называемого спина электрона.

Но что такое спин электрона?

В 1925 году английские физики Дж. Уленбек и С. Гоудсмит для объяснения тонкой структуры линий в оптических спектрах некоторых элементов предложили гипотезу, согласно которой каждый электрон вращается вокруг своей собственной оси подобно волчку или веретену. При таком вращении электрон приобретает некоторый момент импульса, который и получил название спина (в переводе с английского спин означает вращение, веретено). Поскольку вращение может происходить по часовой стрелке или против, то и спин (иначе говоря, вектор момента импульса) может иметь два направления. В единицах 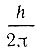спин равен ¹/₂, а благодаря различным направлениям имеет знак "+" или "-". Таким образом, ориентация электрона на орбите определяется спиновым квантовым числом о, равным ±¹/₂. Отметим, что и ориентация спина, как и ориентация орбиты электрона, не влияет на энергию атома водорода, находящегося в свободном состоянии.

Более поздние исследования и расчеты показали, что объяснить спин электрона простым вращением его вокруг оси нельзя. При подсчете угловой скорости вращения электрона для объяснения экспериментальных данных выяснилось, что линейная скорость точек, лежащих на экваторе электрона (в предположении, что электрон имеет шарообразную форму), должна быть больше скорости света, чего не может быть. Спин является некоторой неотъемлемой характеристикой электрона, такой, например, как его масса или заряд.

Квантовые числа - адрес электрона в атоме. Итак, мы выяснили, что для описания движения электрона в атоме, или, как говорят физики, для определения состояния электрона в атоме, необходимо задать набор из четырех квантовых чисел: n, l, m и σ.

Главное квантовое число n определяет, грубо говоря, размеры электронной орбиты. Чем больше n, тем большее пространство охватывает соответствующее электронное облако. Задаваясь значением n, мы тем самым определяем номер электронной оболочки атома. Само число n может принимать любые целочисленные значения от 1 до ∞:

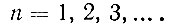
Орбитальное квантовое число l определяет форму электронного облака. Из всей совокупности орбит, относящихся к одному и тому же значению n, орбитальное число l выделяет орбиты, имеющие одинаковую форму. Каждому значению l соответствует своя подоболочка. Число подоболочек равно n, так как l может принимать значения от 0 до (n - 1):

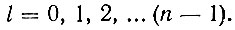
Магнитное квантовое число m определяет пространственную ориентацию орбиты в группе орбит, имеющих одинаковую форму, то есть относящихся к одной подоболочке. В каждой подоболочке насчитывается (2l + 1) различно ориентированных орбит, поскольку m может принимать значения от 0 до ±l:

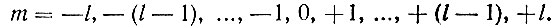
Наконец, спиновое квантовое число а определяет ориентацию спина электрона на заданной орбите. Значений у σ всего два:

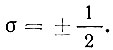
Рассматривая атом водорода и оперируя понятиями "оболочка", "подоболочка", "орбита", мы говорили не столько о строении атома, сколько о возможностях, открывающихся перед единственным электроном, содержащимся в этом атоме. Электрон в атоме водорода может переходить с оболочки на оболочку и с орбиты на орбиту в пределах одной оболочки.

Гораздо сложнее оказывается картина распределения электронов и возможностей их переходов в многоэлектронных атомах.