§ 8. Электрическая проводимость металлов

Наиболее полно и точно явление электрической проводимости металлов описывает квантовая теория твердых тел. Однако для выяснения наиболее общих вопросов можно ограничиться и рассмотрением на основе классической электронной теории. Согласно этой теории совокупность электронов в кристалле можно с известным приближением уподобить идеальному газу, считая движение электронов подчиняющимся законам классической механики. При этом взаимодействие электронов между собой не рассматривается вообще, а взаимодействие электронов с ионами кристаллической решетки сводится к обычным упругим столкновениям.

Металлы содержат огромное число свободных электронов, перемещающихся в межузельном пространстве кристалла. В 1 см³ насчитывается около 10²³ атомов. Следовательно, при валентности металла Z концентрация n свободных электронов, называемых еще электронами проводимости, равна 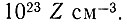. Все они находятся в беспорядочном хаотическом тепловом движении, перемещаясь в пространстве кристалла с колоссальной скоростью, среднее значение которой около 10⁸ см/с. В силу хаотичности теплового движения число электронов, двигающихся в каком-либо направлении, в среднем всегда равно числу электронов, двигающихся во встречном направлении, благодаря чему в отсутствие внешнего электрического поля заряд, переносимый электронами через любое сечение кристалла, равен нулю. Под действием электрического поля каждый электрон приобретает дополнительную скорость, благодаря чему весь коллектив электронов в металле начинает перемещаться в направлении, противоположном направлению напряженности приложенного поля. Появление направленного движения электронов и определяет возникновение в проводнике электрического тока.

На каждый электрон электрическое поле напряженностью Е действует с силой F = eE. Под действием этой силы электрон приобретает ускорение

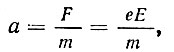
где e - заряд электрона, а m - его масса.

Согласно законам классической механики в свободном пространстве скорость электронов возрастала бы неограниченно; то же наблюдалось бы при их движении в строго периодическом поле (например, в идеальном кристалле с покоящимися в узлах атомами).

В действительности же благодаря нарушениям периодичности в потенциальном поле решетки направленное перемещение электронов в кристалле оказывается совсем незначительным. Нарушения эти в первую очередь связаны с тепловыми колебаниями атомов (в случае металлов - атомных остатков) в узлах кристаллической решетки (при этом амплитуда колебаний тем больше, чем выше температура кристалла). Кроме того, в кристалле всегда имеются различные дефекты, обусловленные наличием атомов примесей, пустых мест в узлах, атомов в междоузлиях, дислокаций. Влияют также границы блоков кристаллов, трещины, полости и т. д.

В этих условиях электроны все время испытывают столкновения и растрачивают приобретенную в электрическом поле энергию. Поэтому в действительности скорость электронов под действием силы внешнего поля увеличивается только на участке между двумя столкновениями. Средняя длина этого участка называется длиной свободного пробега электрона и обозначается через λ.

Итак, ускоряясь на длине свободного пробега, электрон приобретает дополнительную скорость направленного движения

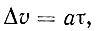
где τ - время свободного пробега, или среднее время между двумя последовательными соударениями электрона с дефектами. Зная длину свободного пробега λ, можно время свободного пробега τ вычислить по формуле

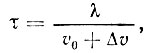
где υ₀ - скорость хаотического теплового движения электрона. Длина свободного пробега электрона λ обычно очень мала и не превышает 10^-5 см. Поэтому малыми оказываются и время свободного пробега τ, и сама добавка скорости Δυ. Так как 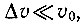то

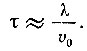
Принимая, что при столкновении с дефектом электрон практически полностью теряет скорость направленного движения, можно среднюю скорость направленного движения, называемую скоростью дрейфа, выразить так:

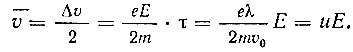
Коэффициент пропорциональности

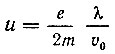
между средней скоростью дрейфа 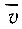и напряженностью поля Е называется подвижностью электронов.

Название этой величины точно отражает ее физический смысл: подвижность - это скорость дрейфа, которую приобретают электроны в электрическом поле единичной напряженности. Более строгий расчет, учитывающий тот факт, что и при хаотическом тепловом движении электроны перемещаются не с постоянной скоростью υ₀, а имеют различные скорости, приводит к вдвое большему значению для подвижности электронов:

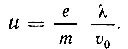
Соответственно и для скорости дрейфа более точным является выражение

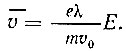
Найдем теперь выражение для плотности тока в металлах. Так как под действием внешнего электрического поля электроны приобретают дополнительную скорость дрейфа 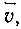то за единицу времени через любую площадку, перпендикулярную напряженности поля, пройдут все электроны, отстоящие от этой площадки на расстоянии, не превосходящем 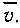Через площадку площадью S за то же время пройдут все электроны, заключенные в объеме параллелепипеда длиной 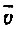(рис. 15). Если концентрация свободных электронов в металле n, то число их в объеме этого параллелепипеда будет равно 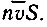. Плотность тока, определяемая зарядом, перенесенным этими электронами через единичную площадь, выразится так:

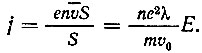
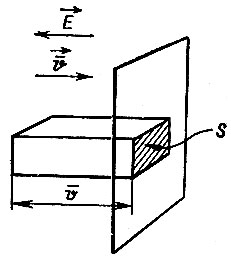
Рис. 15

Отношение плотности тока к напряженности поля, вызвавшего появление этого тока, называется удельной электрической проводимостью (обозначается через σ). Очевидно, что

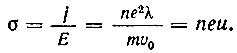
Величина ρ, обратная удельной электрической проводимости, называется удельным электрическим сопротивлением:

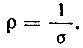
Обратим внимание на то, что возникновение электрического тока в проводнике четко связано с появлением дрейфа электронов. Скорость дрейфа оказывается очень небольшой - в реальных электрических полях ее значение обычно не превышает скорости пешехода. В то же время ток распространяется по проводам практически мгновенно и появляется во всех участках замкнутой цепи почти одновременно. Объясняется это колоссальной скоростью распространения самого электрического поля. При включении источника напряжения электрическое поле приходит в самые удаленные места рассматриваемой цепи со скоростью света и вызывает появление дрейфового перемещения сразу у всего коллектива электронов.