2.2. Частотообразование

Выше указывалось, что наиболее простой способ построения системы (рис. 2.1) является лишь частным случаем общего метода. Поэтому будем строить систему по декадному принципу, т. е. условимся, что с МОЧ на синтезатор подаются три сетки по десять опорных частот f'_qi, f"_qi и f'''_qi (где i = 1, 2, 3, ..., 10 выбирается в каждой сетке независимо от других), а если необходимо, то и ряд других опорных частот f_qj при j = 0, 1, 2, ...

Предположим для общности построения схемы, что умножение и деление частот происходит только в МОЧ (целесообразность этого будет показана в § 7.4). Тогда можно утверждать, что вне зависимости от примененных принципов и схем фильтрации и усиления (за исключением ЧАП) выходная частота системы всегда равна алгебраической сумме

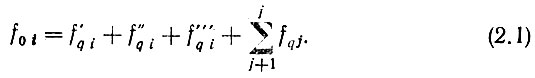
Так как принята декадная система, можно считать, что шаг дискретности сеток опорных частот

Но, с другой стороны, поскольку в устройстве имеется только один эталон частоты, то все частоты и частотные интервалы кратны частоте эталона f_q0. Поэтому

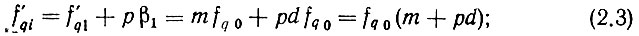
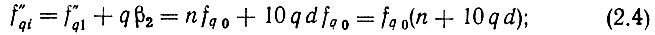
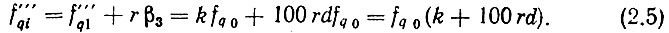
Так как β₁ = β₀ самая малая частота в системе сеток, для упрощения анализа пока примем, что частота эталона fq₀ = β₀, т. е. d = 1. При этом ур-ния (2.3)-(2.5) примут вид:

а основное уравнение системы (2.1) запишется следующим образом:

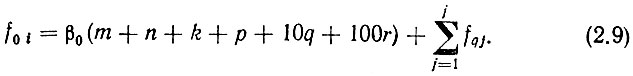
Частоты f_qj также кратны частоте f_q0 и служат для различных сдвигов частот в системе ("сдвиговые частоты"). Они, как очевидно, могут определяться только в процессе расчетов системы конкретного вида. Коэффициенты p, q и r по самому определению декадной системы должны принимать значения в пределах 0-9. Что же касается коэффициентов m, n и k, то их выбор определяется как частотным диапазоном, так и шагом дискретности выходных частот системы β₀. Решая задачу в общем виде, невозможно найти точные численные значения этих коэффициентов. Однако целесообразно установить соотношения между ними и определить их порядок.

Не рассматривая пока подавления побочных составляющих, следует, однако, помнить, что возможности реальных фильтров конечны, т. е., с одной стороны, трудно создать фильтры с очень узкой полосой фильтрации, а с другой, - не менее трудно создать весьма широкополосные переключаемые (перестраиваемые) фильтры.

Если предположить, что, начиная с метровых волн, во всех диапазонах можно осуществить одинаковую максимальную относительную широкополосность фильтров δD_ф, то можно записать условия: 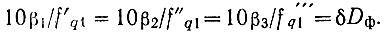Или с учетом (2.2) 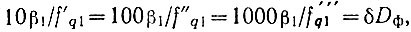а отсюда

С учетом (2.10) выражения (2.6)-(2.8) запишутся в виде:

а основное уравнение - в виде

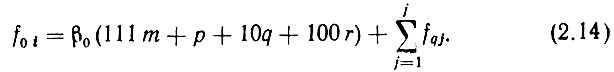
Из (2.14) можно определить порядок коэффициентов m, n и k. Действительно, 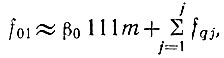откуда

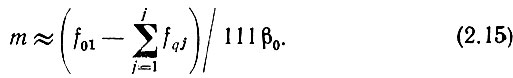
Положив в (2.15) f₀₁ = 5000 МГц (середина диапазона СМВ), β₀ = 1 МГц (наиболее вероятный минимальный шаг дискретности частот в СМВ диапазоне) и приняв сумму сдвиговых частот равной нулю, получим m ≈ 50. Соответственно n ≈ 500 и k ≈ 5000. При этом δD_ф ≈ 0,2, что еще не препятствует серийно способности фильтров, а полоса фильтрации П_фа ≈ 0,04, т. е. также реальная величина.

До сих пор предполагалось, что в системе частоты 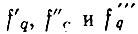суммируются арифметически, т. е. структурная схема синтезатора должна выглядеть так, как изображено на рис. 2.2а. С точки зрения частотообразования эта схема довольно удобна, так как расширяет диапазон ЯФУ₄ по сравнению с ЯФУ₂ и ЯФУ₅ по сравнению с ЯФУ₃ примерно лишь на 10%. Относительные полосы фильтрации ЯФУ₄ и ЯФУ₅ могут быть соответственно больше, чем у ЯФУ₂ и ЯФУ₃ и достигать 0,2. При этом, очевидно, суммирование должно выполняться в порядке последовательного нарастания номинальных значений опорных частот.

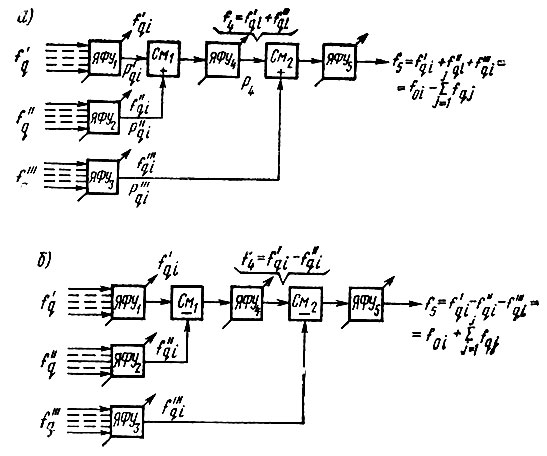
Рис. 2.2. Структурные схемы синтезатора: а) со сложением опорных частот; б) с вычитанием опорных частот

Как вполне очевидно, все изложенное остается в силе, если в смесителях схемы рис. 2.2а производить вычитание частот при сохранении соотношений (2.10), т. е. 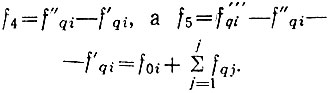В этом смысле структурная схема рис. 2.2а оказывается универсальной, а высказанное положение об алгебраическом суммировании - справедливым.

Заметим, что при таком методе построения системы ее полоса пропускания последовательно расширяется. Если иметь в виду, что шумовая полоса пропорциональна полосе пропускания, то в системе рис. 2.2а мощность шума на выходе синтезатора будет велика. Этот недостаток можно устранить применением последовательного вычитания частот при изменении соотношений (2.10) на обратные (рис. 2.2б). В такой системе по сравнению с системой рис. 2.2а полосу пропускания ЯФУ₄ нужно увеличить в 10 раз или оставить прежней, но при этом в 10 раз увеличить число перестроек этой ячейки. В ЯФУ₅ полоса пропускания должна быть уменьшена в 10 раз и одновременно во столько же раз увеличено число перестроек, либо при уменьшении полосы пропускания ЯФУ₅ в 100 раз число перестроек этой ячейки должно быть увеличено также в 100 раз. Таким образом, сужение полосы пропускания системы достигается за счет усложнения последней, увеличения числа перестроек и сужения полосы фильтрации ЯФУ₅.

Так как окончательно выбрать оптимальную структурную схему синтезатора можно только при учете остальных, требований, перечисленных в конце предыдущего параграфа, остановимся пока на двух рассмотренных выше схемах и введем в них для примера одну сдвиговую частоту. Ее можно ввести в любую точку системы, учитывая только правило последовательности нарастания значений суммируемых частот, например, так, как показано на рис. 2.3 для схемы сложения при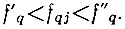

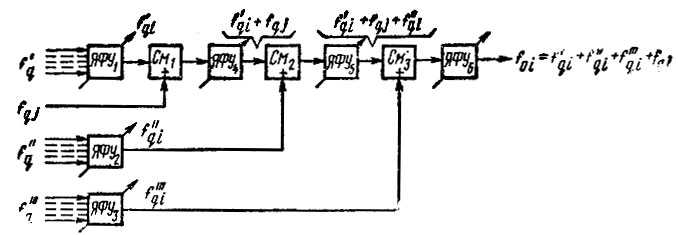
Рис. 2.3. Структурная схема синтезатора при суммировании 'сдвиговой' частоты

В заключение следует указать, что если в качестве ЯФУ используются кольца ФАПЧ с преобразованием частоты, то на каждое из них должна подаваться сдвиговая частота - опорная частота фазового дискриминатора.