3.2. Побочные составляющие

Цифровой синтезатор СВЧ (рис. 3.1б) структурно подобен старшей декаде активного многодекадного синтезатора, в котором используются кольца аналоговой ФАПЧ (рис. 2.7а). Схемно они отличаются наличием в цифровом синтезаторе делителей частоты ДФКД-ДПКД, которые объединяются под общим названием делителя промежуточной частоты ДПЧ. Отсутствие же в схеме рис. 2.7а усилителя первой промежуточной частоты не является принципиальным, так как в любой системе в зависимости от необходимости и возможности технической реализации усилители (в том числе УПЧ, УПТ и т. д.) могут как присутствовать, так и отсутствовать.

Однако по принципу работы указанные системы заметно отличаются друг от друга. Во-первых, если в стационарном режиме значение второй промежуточной частоты в схеме рис. 2.7а постоянно при любой настройке ГУН, то в схеме рис. 3.1б в зависимости от настройки ГУН, оно меняется в пределах Δf_пр2 = β₂. Во-вторых, первым каскадом ДПЧ в схеме рис. 3.1б является формирователь последовательности импульсов с частотой следования Δf_пр2, а на выходе ДПЧ образуется последовательность импульсов с частотой следования f_пр3 = f_пр2/υ. Таким образом, на один вход фазового дискриминатора всегда подается импульсная последовательность. На его второй вход, как будет показано ниже, может подаваться либо также импульсная последовательность, либо периодическое пилообразное напряжение, либо, наконец, синусоидальное напряжение. В-третьих, если в схеме рис. 2.7а номинальное значение частоты колебаний, подаваемых на фазовый дискриминатор, выбирают, исходя из требований оптимального проектирования системы, то в цифровом синтезаторе выбор этой частоты вариациям не подлежит - она должна быть равна f_пр3 = β₀/с. Эти три фактора существенным образом отражаются на характеристиках гармоничности колебаний, шумовых характеристиках и на параметрах кольца ЦФАПЧ.

Характеристики колебаний опорных частот f'_q и f"_q с точки зрения удовлетворения требованиям по коэффициентам гармоничности рассмотрим в следующей главе. Здесь же проанализируем влияние на работу системы колебаний, подаваемых на фазовый дискриминатор. Заметим сначала, что опорная частота f_{q пр3} в подавляющем большинстве случаев практически формируется путем деления эталонной частоты в МОЧ - она является самой низкой частотой в системе. Кроме того, как отмечалось выше, одно или оба колебания, подаваемые на ФД, представляют собой импульсные последовательности. Поэтому на выходе нелинейных элементов фазового дискриминатора всегда присутствуют колебания как частоты f_пр3, так и ее гармоник. Попадая на управляющий вход ГУН, эти колебания модулируют последний по частоте, создавая тем самым побочные колебания на выходе синтезатора.

Как видно, с точки зрения механизма создания этих побочных составляющих процессы в цифровом и активном многодекадном синтезаторах качественно ничем не отличаются. Количественное же отличие весьма значительное. Действительно, выше было показано, что в многодекадной системе значения выходных частот каждых двух соседних декад отличаются примерно на порядок. Как правило, по такому же закону распределяются опорные частоты, подаваемые на декады, в том числе, и частоты, поступающие на фазовые дискриминаторы декад. Следовательно, частота наименьшей побочной составляющей, равная β₀, содержится в опорной частоте младшей декады многодекадного синтезатора в виде шага дискретности этой частоты (сама опорная частота значительно больше β₀). На участке от входа младшей декады до выхода синтезатора эта побочная составляющая подавляется фильтрующими элементами всех декад, т. е. борьба с ней не является чересчур сложной задачей. Иное дело в цифровом синтезаторе, где опорная частота, подаваемая на фазовый дискриминатор, не только непосредственно равна β₀, но в ряде случаев даже меньше ее, так как f_{q пр3} = β₀/с и борьба с этой самой опасной побочной составляющей осуществляется непосредственно кольцом ЦФАПЧ - выходным кольцом синтезатора.

Для анализа процесса подавления указанной побочной составляющей рассмотрим применение в системе фазовых дискриминаторов различных типов. Основной задачей любого фазового дискриминатора является формирование на своем выходе постоянного напряжения Е_ФД, пропорционального разности фаз колебаний Δφ, подаваемых на его входы. В этом плане идеальная характеристика ФД представляется наклонной прямой, продолжающейся в обе стороны от начала координат (кривая 1 на рис. 3.2).

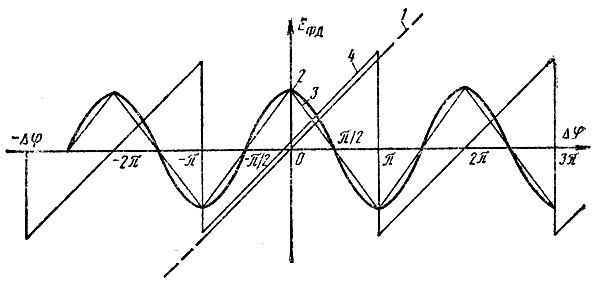
Рис. 3.2. Характеристики фазовых дискриминаторов: 1 - идеальная; 2 - косинусоидальная; 3 - треугольная; 4 - пилообразная

В аналоговых системах ФАПЧ обычно применяются балансные или кольцевые фазовые дискриминаторы, на входы которых подаются синусоидальные колебания. Характеристики таких ФД с учетом начального сдвига фаз между колебаниями на π/2 - косинусоидальные (кривая 2 на рис. 3.2). При равных амплитудах напряжений, подаваемых на такой ФД, характеристика последнего приближается по форме к треугольной (кривая 3 на рис. 3.2). Как видно из рисунка, линейная часть характеристики этого фазового дискриминатора соответствует вариации Δφ ≤ ±π/2. Применение балансного ФД в цифровом синтезаторе потребовало бы подачи на него синусоидального колебания опорной частоты f_{q ФД} с МОЧ и включения узкополосного фильтра между ДПЧ и ФД для выделения первой гармоники частоты следования импульсов с выхода ДПЧ. Такое решение предложено в [П7.2], но его нельзя признать удовлетворительным из-за того, что узкополосный фильтр значительно увеличивает время запаздывания в кольце ЦФАПЧ и тем самым резко ухудшает характеристики последнего.

Намного целесообразнее применить в качестве фазового дискриминатора один из типов временных дискриминаторов. Простейшим временным дискриминатором является триггерный (по терминологии [135] - инерционный). Временные диаграммы, поясняющие работу такого ФД при установившемся синхронизме в системе, изображены на рис. 3.3а. На триггер поступают две последовательности импульсов равных частот следования, но сдвинутые по фазе и, следовательно, во времени. Импульсы одной последовательности U_вх1 опрокидывают триггер (например, из положения логического "О" в положение логической "1"), а импульсы второй последовательности U_вх2 возвращают триггер в исходное состояние. На выходе триггера формируется последовательность импульсов U_вых, длительность которых равна временному сдвигу между импульсами входных последовательностей. Так как, во-первых, этот временной сдвиг пропорционален фазовому сдвигу между подаваемыми на ФД колебаниями (коэффициент пропорциональности 1/2πf_{q ФД}), во-вторых, длительность выходных импульсов равна временному сдвигу и, в-третьих, постоянная составляющая выходной импульсной последовательности, являющаяся выходным параметром ФД, пропорциональна длительности выходных импульсов, можно утверждать, что характеристика триггерного ФД является прямой, в пределах изменения Δφ = ±π, проходящей через начало координат (кривая 4 на рис. 3.2). Как видно из рисунка, эта характеристика в указанных пределах изменения аргумента совпадает с идеальной характеристикой ФД. Заметим, что в фазовом дискриминаторе этого типа осуществляется широтноимпульсная модуляция по закону изменения Δφ.

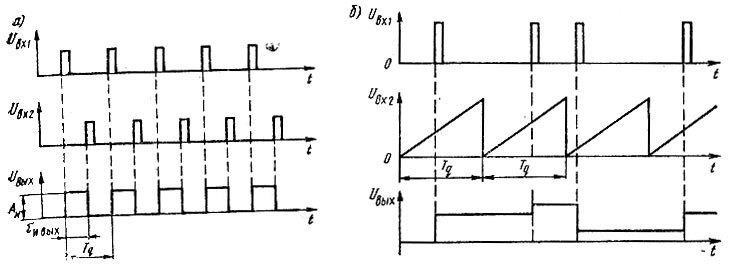
Рис. 3.3. Эпюры напряжений на ФД: а) триггерном; б) типа 'выборка - запоминание'

Однако при всей своей схемной простоте триггерный ФД имеет плохие характеристики. Если, как показано на рис. 3.3а, обозначить длительность импульсов на выходе ФД через τ_{и вых}, их амплитуду - A_и и период следования - T_q = 1/f_{q ФД}, то последовательность выходных импульсов ФД может быть описана рядом Фурье. Амплитуды слагаемых этого ряда, как известно, выражаются следующим образом:

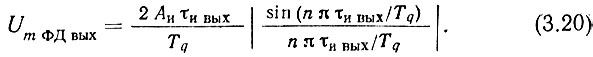
Если задаться монотонной характеристикой фильтра нижних частот, то интерес представит первая гармоника разложения. При n = 1 выражение (3.20) запишется в виде

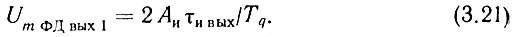
Под влиянием этого напряжения происходит паразитная частотная модуляция ГУН с девиацией

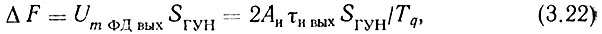
где S_ГУН - крутизна характеристики управления ГУН.

Но в зависимости от Δφ длительность импульсов меняется в пределах 0 ≤ τ_{и вых} ≤ T_q, следовательно, U_{m ФД вых1 макс} = 2А_и и

Так как индекс этой паразитной ЧМ ψ_f << 1, то коэффициент гармоничности колебаний на выходе ГУН

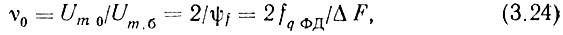
где U_m0 - амплитуда выходных колебаний ГУН; U_mб - амплитуда боковой (побочной) составляющей.

Подставив (3.23) в (3.24), получим

Как следует из (3.25), заданное значение ν_{0 мин} ограничивает увеличение амплитуды импульсов и крутизны характеристики управления ГУН, а также уменьшение частоты f_{q ФД} или шага дискретности β₀.

Анализ кольца ЦФАПЧ с триггерным фазовым дискриминатором, проведенный в [135], показывает следующее. Так как постоянная времени заряда выходной емкости ФД - Т_з значительно превышает длительность импульса τ_и, переходные процессы в кольце оказываются длительными по сравнению с периодом регулирования T_q. Система имеет пониженную помехоустойчивость по отношению к дискретным помехам, так как модуль частотной характеристики кольца на определенной частоте (оп имеет подъем (пик). Частота пика определяется из выражения cos ω_ПТ_q = 0,5(2-|W|), где W - коэффициент передачи кольца, равный произведению коэффициентов передачи всех входящих в кольцо элементов, а его высота - из выражения

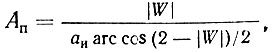
где а_и = τ_и/T₃ - параметр длительности импульса.

Ослабить пик можно, во-первых, уменьшением W, что, однако, приведет к уменьшению быстродействия системы и, во-вторых, увеличением a_и, что, хотя и увеличит быстродействие, но и повысит интенсивность составляющих, кратных частоте регулирования, в выходном напряжении ФД, т. е. опять-таки ухудшит коэффициент гармоничности колебаний.

Большая интенсивность помех с частотами f_{q ФД} и ее гармоник заставляет включать после триггерного ФД весьма узкополосный фильтр нижних частот, что резко сужает полосу пропускания кольца и, таким образом, делает систему весьма инерционной. Из этого следует, что полоса захвата становится малой, собственные шумы ГУН компенсируются плохо, а время установления синхронизма в системе оказывается весьма большим. Так, для хорошего подавления помехи с частотой f_{q ФД} частота среза ФНЧ должна быть примерно 0,1f_{q ФД} [116]. При этом время установления синхронизма оказывается очень большим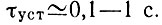

Из изложенного вытекает, что при заданных параметрах системы в цифровых синтезаторах существует предел уменьшения частоты f_{q ФД} или пропорционального ей шага дискретности выходных частот β₀.

Для преодоления этого предела авторы ряда работ [П 1.29], [П 2.31], [П 3.33], [П 4.32], [15] и др. предлагают номинальное значение частоты подаваемых на ФД колебаний выбирать сравнительно большим, а для получения малого шага дискретности выходных частот синтезатора строить ДПКД с дробным коэффициентом деления (ДДПКД). При этом колебание опорной частоты f_{q ФД}, подаваемое на ФД, представляет собой, как и прежде, регулярную импульсную последовательность, а частота следования импульсов с выхода ДДПКД только в среднем равна опорной частоте, т. е. f_ФДср = f_{q ФД}.

Действительно, если выбрать, к примеру, опорную частоту f_{q ФД} = 10β₀ (примем, для наглядности, с = 1), то в простейшей системе ЦФАПЧ коэффициент деления ДПКД υ = f₀/f_{q ФД} = f₀/10β₀. Если теперь перестроить частоту ГУН вверх на β₀, то υ₁ = (f₀ + β₀)/f_qФД = (f₀ + β₀)/10β₀ = υ₀ + 0,1, а в общем случае для перестройки f₀ на aβ₀ (а = 0, 1, ..., 9), υ_a = υ₀ + 0,1 а.

Для осуществления дробного коэффициента деления авторы ДДПКД предлагают следующую методику. В десяти циклах счета деление частоты на υ₀ производить (10 - а) раз, а на (υ₀ + 1) - а раз. Тогда средний за десять циклов коэффициент деления υ_ср = [(10 - a)υ₀ + a(υ₀ + 1)]/10 = υ₀ + 0,1 a = υ_a. Выбирая f_qФД = 100 β₀ и рассуждая аналогично, придем к дробному коэффициенту деления ДДПКД, усредненному за сто периодов счета.

На первый взгляд кажется, что ценой усложнения ДПКД трудности, связанные с получением малого шага дискретности выходных частот в цифровых синтезаторах, преодолены. Однако при детальном рассмотрении процессов в схеме можно выяснить, что частота помех, создающих побочные составляющие, оказывается равной β₀/с и не зависит от выбранной опорной частоты f_qФД. Поэтому ФНЧ оказывается таким же узкополосным, как и в обычной системе ЦФАПЧ со всеми вытекающими отсюда недостатками. На трудности, связанные со сравнением в фазовом дискриминаторе регулярного импульсного процесса с нерегулярным, указывается в ряде публикаций, посвященных цифровым синтезаторам с изменяющимся числом импульсов в периоде счета.

Другим типом временного дискриминатора является безынерционный, работа которого основана на использовании принципа "выборка - запоминание". Она поясняется временными диаграммами, несколько утрированно изображенными на рис. 3.3б. На этом рисунке на один вход фазового дискриминатора подаются импульсы выборки U_вх1 с выхода ДПЧ, а на второй вход - пилообразное напряжение U_вх2 опорной частоты f_qФД = 1/T_q. Импульсы выборки управляют ключами ФД так, что в момент прихода импульса уровень пилообразного напряжения, которого оно достигло в этот момент, запоминается на запоминающем элементе (обычно на емкости) и прикладывается к управляющему электроду ГУН в виде U_вых. Это управляющее напряжение сохраняется на входе ГУН до прихода следующего импульса выборки. Таким образом, если в случае триггерного ФД выходное напряжение требуется усреднять по нескольким периодам, то в данном случае частота ГУН изменяется сразу за один цикл регулирования. Ступенчатое выходное напряжение ФД можно представить как амплитудно-модулированную импульсную последовательность со скважностью, равной единице.

Фазовый дискриминатор типа "выборка - запоминание" может быть представлен последовательно соединенными линейным разностным компаратором, нелинейным элементом, устройством для получения дискретных значений с частотой, равной частоте f_{q ФД} и фиксирующим устройством нулевого порядка [121]. Передаточная функция по Лапласу фиксирующего устройства выражается как

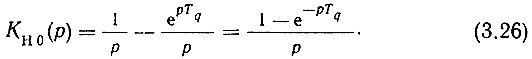
Заменяя в (3.26) p на iω, нетрудно получить амплитудно-частотную характеристику (АЧХ) фиксирующего устройства, которая представляет собой модуль передаточной функции

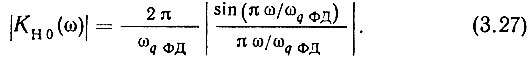
Для получения АЧХ всего фазового дискриминатора нужно (3.27) умножить на крутизну характеристики ФД:

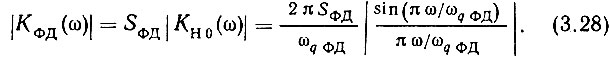
График функции (3.28) представлен на рис. 3.4. Из этого графика следует, что коэффициент передачи идеального ФД типа "выборка - запоминание" для помех с частотами, близкими к опорной, и ее гармониками равен нулю. Реальный ФД имеет паразитные проходные емкости ключей и неидеальное запоминание напряжения между двумя импульсами выборки, а поэтому частично пропускает на свой выход указанные помехи. Однако использование в данном ФД в качестве ключей полевых транзисторов позволяет ослабить помехи в КВ и УКВ системах до уровня порядка 110 дБ по сравнению с помехами в триггерном ФД [112].

Рис. 3.4. Частотная характеристика фиксатора нулевого порядка

Таким образом, если на выходе триггерного фазового дискриминатора необходимо включение узкополосного ФНЧ, то безынерционный ФД с точки зрения подавления побочных составляющих, в принципе, вообще не требует ФНЧ. Однако, как будет показано ниже, для обеспечения других характеристик системы включение пропорционально-интегрирующего фильтра и после этого ФД необходимо.

Кроме указанных достоинств, следует отметить, что благодаря применению безынерционного фазового дискриминатора при коэффициенте передачи замкнутого кольца W₀₁, близкого к единице, АЧХ не имеет пика и, таким образом, помехи здесь не подчеркиваются [135].

Отметим особенность применения ФД типа "выборка - запоминание" в цифровых синтезаторах СВЧ. При сравнительно высокой опорной частоте f_qФД ≥ 500 кГц, что следует считать характерным для систем сантиметрового и отчасти дециметрового диапазонов, формирование пилообразного напряжения с высокой линейностью наклонного участка и крутым спадом оказывается технически очень трудной задачей. Поскольку реальное пилообразное напряжение весьма далеко от идеального, часто целесообразно вместо него использовать синусоидальное колебание опорной частоты, а импульсы по-прежнему подавать на ФД с ДПЧ. При этом описанная выше работа ФД и характер выходного напряжения последнего сохраняется, но форма характеристики ФД окажется косинусоидальной, а ее размах сократится до ±π/2.

Итак, для обеспечения заданных коэффициентов гармоничности выходных колебаний цифрового синтезатора СВЧ выбираем структурную схему рис. 3.1б с безынерционным фазовым дискриминатором типа "выборка - запоминание".