5.2. Устройства подавления пассивных помех

Как указывалось выше, компенсация сигналов пассивных помех возможна либо за счет подавления сигналов, неизменных по амплитуде от периода к периоду повторения, либо за счет режекции составляющих частоты повторения в спектре сигналов. В первом случае используются системы череспериодного вычитания или череспериодной компенсации, во втором - режекторные гребенчатые фильтры. Классификация систем подавления пассивных помех показана на рис. 5.3.

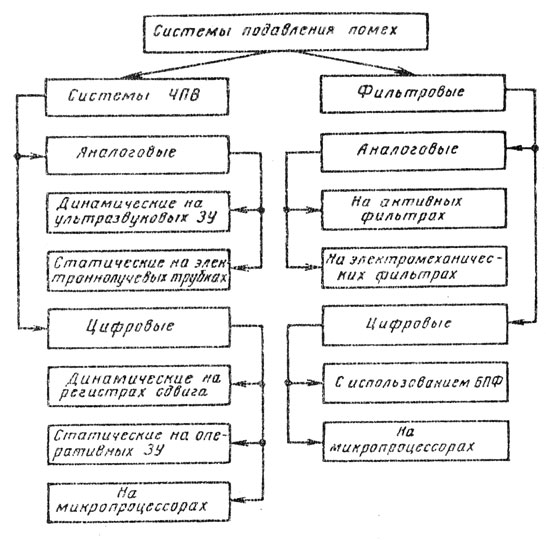
Рис. 5.3

Рассмотрим простейшее устройство подавления пассивных помех (рис. 5.4) - однократную систему ЧПВ-ЧПК и покажем, что она обладает режекторной гребенчатой частотной характеристикой. В соответствии с обозначениями рис. 5.4

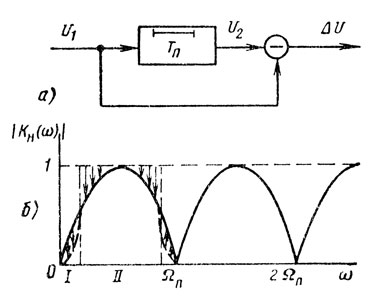
Рис. 5.4

Тогда, если U₁(t) = F(р) и

то

Знак соответствия = означает, что функция времени преобразована в функцию оператора р или наоборот. Следовательно, К(р) = 1 - е^-рТ_п.

Переходя от р к iω, получаем

Таким образом,

К(ω) = |K(iω)| = 2 sin (ωT_п/2) - амплитудно-частотная характеристика; φ(ω) = arg К(iω) = (π - ωT_п)/2 - фазочастотная характеристика.

На рис. 5.4 показана нормированная амплитудно-частотная характеристика (АЧХ) однократной системы ЧПВ-ЧПК |K_н(ω)|. Штриховой линией показана характеристика оптимальной системы обеления пассивной помехи - оптимального РГФ. Видно, что на участке I, т. е. в полосах режекции, для оптимального РГФ |K_н(f)|² = G_nn^-1(f), а для однократной ЧПВ |К_н(f)| = sin πfT_п. Следовательно, имеется проигрыш по отношению к оптимальному РГФ и пассивная помеха не обеляется. На участке II, т. е. в полосе прозрачности ЧПВ, также имеется проигрыш по сравнению с оптимальным РГФ, так как она ослабляет сигналы полезных целей и требуется устройство с более равномерной АЧХ. Наконец, за счет периодического повторения в АЧХ на частотной оси полос режекции возникают так называемые "слепые" скорости, когда сигналы целей, движущихся со скоростями, дающими доплеровскую поправку, которая равна или кратна частоте повторения, подавляются как сигналы неподвижных целей, поскольку компоненты этих сигналов попадают в полосу режекции. В самом деле, нули частотной характеристики РГФ соответствуют условию

где k = 0, 1, 2, ... Следовательно,

ω_k = ω_д = 2π ^2υ_rk/_λ, откуда

Разработка систем подавления или РГФ, более совершенных по сравнению с однократными ЧПВ, велась в следующих направлениях. Прежде всего - это использование многократных или многоступенчатых систем ЧПВ-ЧПК для улучшения обеления пассивных помех. На рис. 5.5 показаны последовательное (а) и параллельное (б) построения многократных систем ЧПК и изменение характера АЧХ (в) таких систем при увеличении кратности вычитания. В общем случае на выходе системы n-кратного вычитания образуется сигнал (остаток вычитания) вида

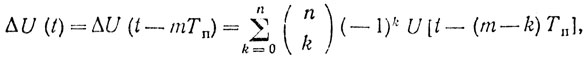(5.11)

где (ⁿ_k) = С^k_n - биномиальный коэффициент, а сама n-кратная система череспериодного вычитания имеет следующую АЧХ

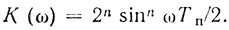(5.12)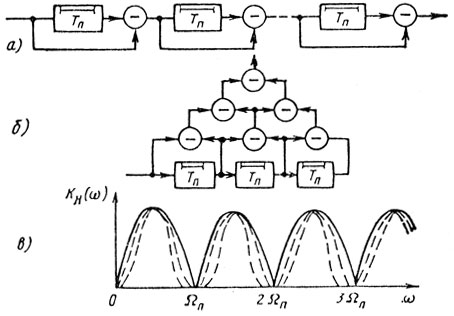

Рис. 5.5

Видно, что по мере увеличения кратности вычитания АЧХ становится все более неравномерной в полосе прозрачности.

Для улучшения равномерности АЧХ в полосе прозрачности используют РГФ с прямыми и обратными связями, т. е. рекурсивные РГФ [1, 23]. Примеры РГФ показаны на рис 5.6. Коэффициенты передачи таких РГФ:

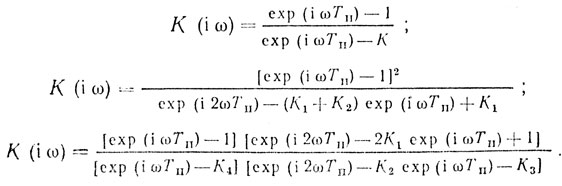
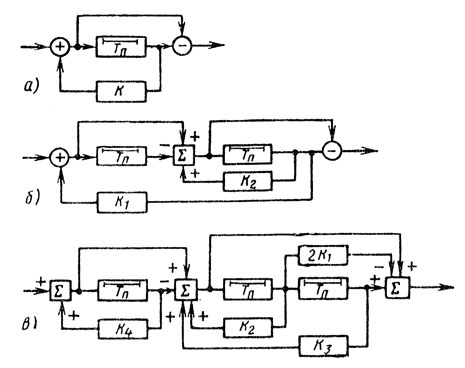
Рис. 5.6

Частотные характеристики рекурсивных систем ЧПВ, приведенных на рис. 5.6, представлены на рис. 5.7. На рис. 5.8 представлены зависимости коэффициента улучшения К_у этих систем от коэффициентов обратной связи и числа импульсов в пачке n [8].

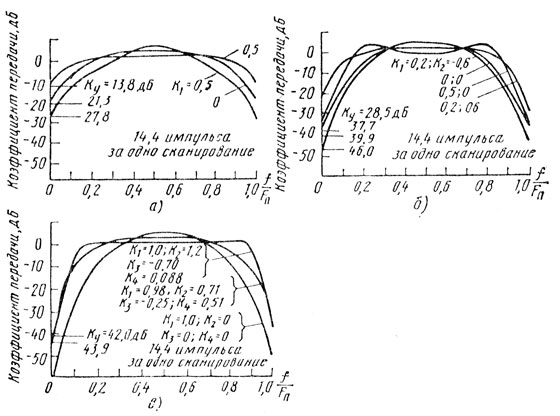
Рис. 5.7

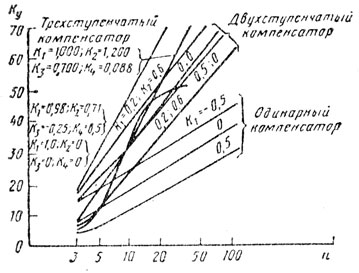
Рис. 5.8

Для борьбы со "слепыми" скоростями можно в соответствии с соотношением (5.10) изменять во времени (вобулировать) либо длину волны (несущую частоту), либо частоту повторения (период повторения). Поскольку при вобуляции несущей частоты требуется одновременно перестраивать генератор радиочастоты (передатчик), входные цепи приемника и гетеродин, то обычно предпочитают использовать вобуляцию частоты повторения. На рис. 5.9 иллюстрируется способ осуществления вобуляции с двумя фиксированными частотами и периодами повторения F_п1 - Т_п1, F_п2 - Т_п2. Поясняется идея вобуляции, заключающаяся в приведении выходного сигнала к единому исходному периоду повторения Т_п. Можно показать, что неравномерность АЧХ или, точнее, скоростной характеристики ΔК_н зависит от коэффициента вобуляции К_в = Т_п1/Т_п2, т. е ΔК_н = f(К_в).

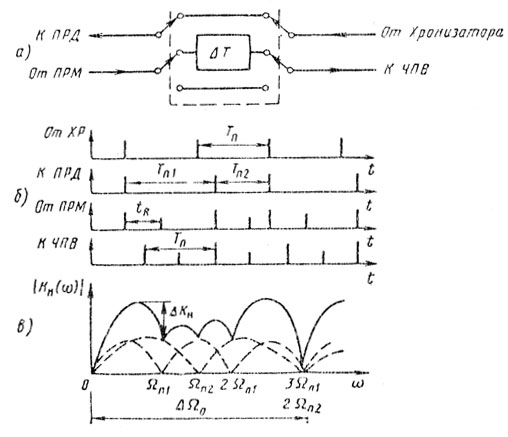
Рис. 5.9

На рис. 5.9, в показан простейший пример скоростной характеристики однократной ЧПВ при двухступенчатой вобуляции периода повторения. Первый нуль (или первая "слепая" скорость) результирующей частотной или скоростной характеристики определяются простым условием

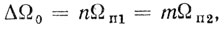(5.13)

где n и m - простые целые не разлагаемые на множители числа.

Лучшие результаты можно иметь, увеличивая число ступеней вобуляции периода Т_п. В ряде работ [8] показано, что увеличение числа ступеней T_пi при вобуляции приводит к уменьшению глубины изрезанности скоростной характеристики системы и увеличению числа пиков осцилляции на ее вершине. Расчет первой "слепой" скорости v01 при многоступенчатой вобуляции T_п1, T_п2, ..., T_пi, ..., T_пN производится на основании соотношения

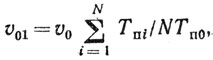(5.14)

где υ₀ - "слепая" скорость при периоде повторения Т_п0 и при отсутствии вобуляции периода.

Применение при вобуляции частоты повторения обратных связей в системах ЧПВ нецелесообразно, так как они мало влияют на форму скоростной характеристики, которая в этом случае определяется законом вобуляции периода [8]. Наконец, следует отметить, что вобуляция частоты повторения несколько понижает коэффициент улучшения. В [8] предлагается эмпирическая формула для расчета коэффициента улучшения в зависимости от глубины вобуляции периода:

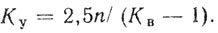(5.15)

В работе [52] показано, что для двухкратной системы вычитания и двухступенчатой вобуляции периода повторения (Т_п1, Т_п2, причем Т_п = 0,5 (Т_п1 + Т_п2), а К_в = Т_п2/Т_п2) при аппроксимации корреляционной функции помехи гауссовской кривой ухудшение К_у определяется соотношением

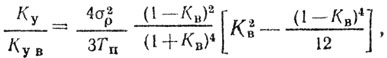(5.16)

где К_у и К_{у в} - коэффициенты улучшения без вобуляции и при вобуляции соответственно; σ²_р - дисперсия гауссовской аппроксимации корреляционной функции.

Для компенсации снижения коэффициента улучшения в ряде работ предлагается использовать переменную во времени весовую обработку с коэффициентами, отличными от биномиальных [8]. Однако это приводит к дополнительным усложнениям системы подавления пассивных помех.

Техническая реализация устройств СДЦ определяется элементной базой (цифровой или аналоговой), а также и тем, с сигналами промежуточной частоты или видеосигналами оперирует устройство подавления.

В аналоговых системах подавления в качестве элементов задержки или запоминания используются ультразвуковые линии задержки и потенциалоскопы. В цифровых системах для тех же целей применяются регистры сдвига и оперативные запоминающие устройства.

На промежуточной частоте при использовании ультразвуковых линий задержки (УЛЗ) построение систем ЧПВ упрощается, поскольку можно подавать сигналы на УЛЗ непосредственно с УПЧ приемника. Таким образом, в системах ЧПВ осуществляется вычитание сигналов на несущей частоте с точностью до фазы заполнения импульсов. Для компенсации нестабильности времени задержки из-за изменения температуры требуется подстройка частоты заполнения.

Схема ЧПВ на промежуточной частоте (или так называемый векторный компенсатор) [8] показана на рис. 5.10. После усилителя-ограничителя (УО) в смесителе осуществляется перевод частоты радиоимпульсов на величину f₁ - f₂, где f₁ - промежуточная частота, а f₂ - частота управляемого генератора (Г). Разностная частота f₁ - f₂ совпадает с резонансной частотой пьезопреобразователей УЛЗ.

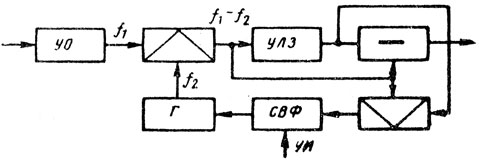
Рис. 5.10

Подстройка фазовых соотношений для поддержания постоянства задержки при вариации температуры осуществляется путем перестройки частоты f₂ Г цепью регулировки таким образом, чтобы выполнялось соотношение 2π (f₁ - f₂)T₃ = const. С помощью схемы выборки и фиксации (СВФ), запускаемой управляющим импульсом (УИ), частота генератора подстраивается в пределах начала дистанции по мощным сигналам местных объектов.

В настоящее время для создания нужной формы частотной характеристики все чаще прибегают к комбинированию выходных сигналов различных систем ЧПВ. Примером служит система TACCAR, описанная в [8]. Эта система складывает выходные сигналы двух однократных систем ЧПВ с балансным фазовым детектором (БФД) и обычным ФД при подаче опорного сигнала со сдвигом фаз на 90° (рис. 4.11). Формирование частотной характеристики показано на рис. 5.11, б, где даны зависимости выходных сигналов в точках 1, 2 и 3 схемы рис. 5.11, а как функции набегов фазы за период.

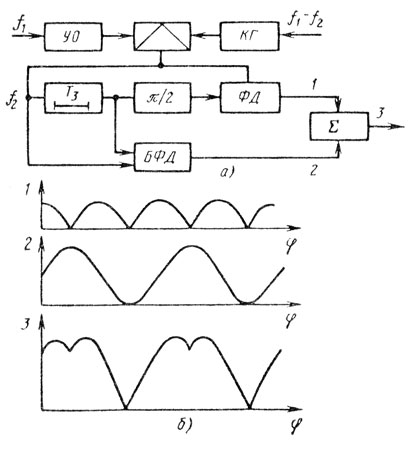
Рис. 5.11

При подавлении пассивных помех с помощью режекторного фильтра после детектирования (на видеочастоте) для устранения влияния начальной фазы отраженного сигнала, а также для борьбы с так называемыми "слепыми" фазами и сохранения фазовых соотношений используют обработку сигналов в квадратурных каналах. В этом случае в каждый из квадратурных каналов вводится свой РГФ или подавитель пассивных помех, работающий на видеочастоте.

В аналоговых системах подавления пассивных помех, работающих после детектора, в качестве элемента задержки чаще всего используются УЛЗ и потенциалоскопы (ПС) [1].

Особенностями УЛЗ являются:

1) необходимость пропускания через УЛЗ радиоимпульсов, что определяется свойствами передающего и приемного пьезопреобразователей;

2) затухание сигнала в УЛЗ на 60-80 дБ из-за рассогласования пьезопреобразователей со звукопроводом, поглощения в звукопроводе и потерь на его стенках;

3) зависимость задержки от температуры;

4) наличие многократного прохождения сигнала в УЛЗ;

5) влияние на УЛЗ механических и акустических воздействий.

Все эти особенности приводят к усложнению схемы РГФ на УЛЗ (рис. 5.12) в однократной одноканальной системе ЧПВ.

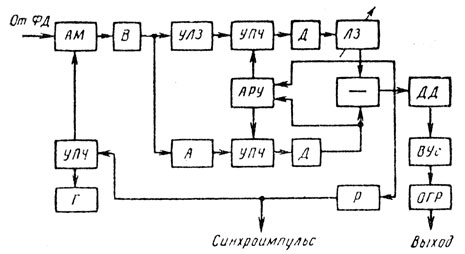
Рис. 5.12

Генератор (Г) формирует колебания с частотой, совпадающей с резонансной частотой настройки пьезопреобразователей УЛЗ и лежащей обычно в диапазоне промежуточных частот. УПЧ, ампли тудный модулятор (AM) и возбудитель (В) обеспечивают заполнение видеоимпульсов несущим колебанием и возбуждение пьезопреобразователя УЛЗ. УПЧ после УЛЗ компенсирует затухание в линии и одновременно вносит некоторые искажения и дополнительную задержку. Идентичный УПЧ в канале без задержки вносит в незадержанный сигнал такие же искажения. Аттенюатор (А) создает в прямом канале такое же ослабление сигнала, как и УЛЗ. После обработки в детекторе (Д) видеоимпульсы вычитаются и нескомпенсированный остаток проходит через двухтактный детектор (ДД), видеоусилитель (ВУс) и ограничитель (ОГР) на выход. Дифференциальное АРУ обеспечивает одинаковое усиление в прямом и задерживающем каналах.

Поскольку УЛЗ является динамическим устройством памяти и подвержена температурным воздействиям, то синхроимпульсы для передатчика формируются путем регенерации импульсов, прошедших через УЛЗ. Для этого в схеме предусмотрена цепочка: регенератор импульсов (Р), УПЧ, АМ, В, УЛЗ, УПЧ, Д, элемент регулируемой дополнительной задержки (ЛЗ).

Как видно, система ЧПВ на УЛЗ требует для технической реализации большого числа дополнительных элементов и поэтому достаточно сложна и громоздка. В настоящее время чаще всего применяются УЛЗ с твердым звукопроводом из плавленого кварца, магниевых сплавов и монокристаллов солей [1].

Особенности потенциалоскопа:

1) сигнал запоминается в виде электрического заряда, т. е. в виде видеоимпульсов на диэлектрической мишени;

2) имеются цепи управления движением электронного луча;

3) неравномерность электрических свойств мишени;

4) наличие значительных межэлектродных паразитных емкостей.

Структурная схема однократной ЧПК на ПС показана на рис. 5.13, где ГР - генератор развертки, УВР - блок управления вертикальной разверткой, УГР - блок управления горизонтальной разверткой. Построение системы ЧПК на потенциалоскопе определяется особенностями функционирования последнего. Потенциалоскоп с барьерной или тормозящей сеткой (ТС) запоминает входные импульсы в виде электрических зарядов, создающих соответствующий потенциальный рельеф на мишени (М). При изменении от периода к периоду повторения входных сигналов сигнальной пластины (СП) возникает излишек либо недостаток заряда, которые восполняются за счет увеличения или уменьшения тока вторичной электронной эмиссии мишени. Увеличение или уменьшение этого тока, замыкающегося через коллектор, и создает на коллекторном резисторе некомпенсированный остаток. При неизменности за период повторения входных сигналов перезаряда мишени нет, ток коллектора неизменен и, следовательно, происходит компенсация этих входных сигналов.

Рис. 5.13

Недостатком потенциалоскопических ЧПК является малый динамический диапазон, определяемый отношением равновесного потенциала мишени U_р и уровнем шума σ_М запоминаемого сигнала, который обусловлен неравномерностью электрических свойств диэлектрической мишени. Таким образом,

Другим недостатком являются значительные межэлектродные емкости, сужающие полосу пропускания такого устройства и не позволяющие работать короткими импульсами. Это Обстоятельство, в частности, привело к тому, что при компенсации помехи на несущей (промежуточной) частоте единственным подходящим для этого устройством остается ЧПК на УЛЗ.

В настоящее время наибольшее распространение получили цифровые системы подавления помех (ЦСДЦ, ЦРГФ). Основной особенностью ЦСДЦ является необходимость предварительного преобразования сигналов в цифровую форму с помощью АЦП. При этом используется двойная дискретизация сигнала: по времени с квантом Δt = τ и по уровню с квантом ΔU = σ_ш.

Динамический диапазон помехи по входу d = U_max/U_min = U_max/σ_ш. Число двоичных разрядов кода m = [log₂ d] [23]. Следовательно, отношение динамического диапазона входных сигналов или помех к числу двоичных разрядов

Таким образом, если известен ожидаемый динамический диапазон, то можно найти число разрядов преобразователя:

Быстродействие преобразователя определяется требованием затрат времени на преобразование меньшего, чем дли тельность временного кванта, т. е.

Кроме того, поскольку быстродействия АЦП недостаточно для преобразования сигналов промежуточной частоты, обычно переходят к построению ЦСДЦ и ЦРГФ в виде комплексных фильтров с двумя квадратурными каналами, в которых используются два АЦП.

После подавления помех применяют оптимальную обработку сигнала на фоне белого шума. Обычно в системах ЦСДЦ это достигается за счет когерентного либо некогерентного накопления модулей или квадратов остатков вычитания. При когерентном накоплении вводится поправка в фазу сигнала для компенсации движения цели. В самом деле, если известна (измерена) доплеровская поправка частоты ω_д сигнала цели, то набег фазы за период подавления будет ψ = ω_дТ_п. Пусть сигнал приходит в k-м периоде повторения:

где k = 0, 1, 2, ...; ψ₀ - начальная фаза.

Тогда

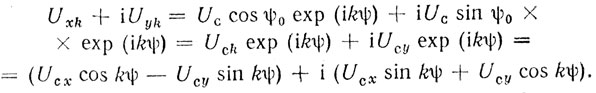
Для компенсации набега фазы ψ нужно подать компенсирующий сигнал υ_k, такой, чтобы U_kυ_k = U_с, т. е. υ_k = U_cU^-1_k, поэтому

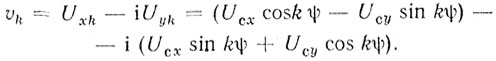(5.19)

Таким образом, в двух квадратурных каналах в каждом k-м периоде повторения по известной величине ψ формируются поправки, обеспечивающие когерентность накопления.

На рис. 5.14 показана структурная схема ЦСДЦ с когерентным интегрированием остатков. Подавление помех в квадратурных каналах осуществляется по соответствующему алгоритму ЦРГФ, состоящим из общего для каждого канала запоминающего устройства (ЗУ) и арифметического устройства (АУ). Когерентное накопление сигналов осуществляется после ввода компенсирующих поправок блоком ввода поправок (БВП) с помощью цифрового полосового гребенчатого фильтра (ЦПГФ) на общем ЗУ и индивидуальных АУ [107].

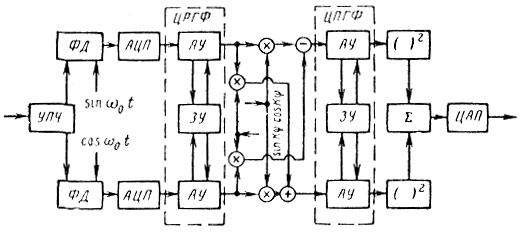
Рис. 5.14

Сложность ввода компенсирующих поправок, особенно в случае одновременной обработки сигналов нескольких целей, приводит к многоканальным системам подавления помех. Упрощение структуры ЦСДЦ возможно при отказе от когерентного накопления и переходе к ЦСДЦ с некогерентным накоплением, структура которой изображена на рис. 5.15 [107].

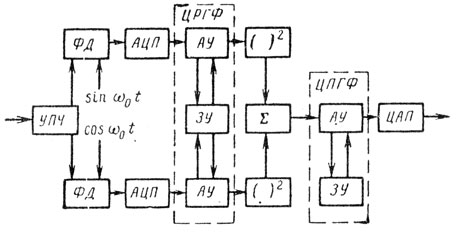
Рис. 5.15

Известно [69], что использование АЦП приводит к ошибкам двух типов: ошибке квантования и ошибке, возникающей вследствие ограничения, когда сигнал на входе превышает максимальный уровень квантования. При оценке работы системы СДЦ обычно используют коэффициент улучшения. При определении требований к АЦП задача значительно упрощается, если использовать коэффициент подавления (К_п) помехи. Чтобы получить искомые количественные соотношения, напомним сначала, что К_п связан с коэффициентом корреляции ρ(τ) помехи. Поэтому ухудшение, вызванное процессом квантования, может быть определено непосредственно при вычислении коэффициента корреляции ρ_п(τ) помехи на выходе АЦП. Аналитическая аппроксимация, используемая здесь, может быть применена к другим системам СДЦ, однако результаты, полученные ниже, относятся исключительно к системам с однократным и двухкратным ЧПВ. Для гауссовских процессов [24]

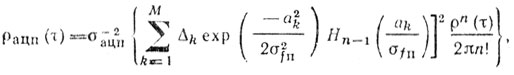(5.20)

где H_n(х) - полином Эрмита n-го порядка; a_i - i-й порог; Δ_j - величина j-го шага квантования; М - общее число уровней квантования; σ²_ацп - средняя мощность квантованного выходного сигнала.

Рассмотрим АЦП (рис. 5.16) с нулевым выходным уровнем (а) и без него (б).

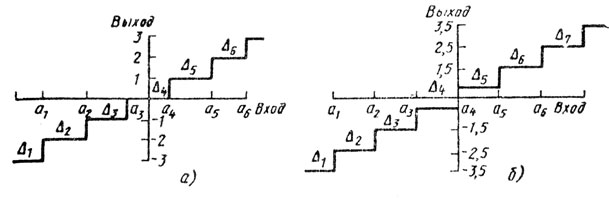
Рис. 5.16

АЦП с нулевым выходным уровнем (М-нечетное). Этот тип АЦП с равномерным квантованием имеет нулевой выходной уровень. Поскольку нормированное расстояние между порогами является постоянным и равным a_k/σ_п = α, а размер шага (без потери общности) можно принять равным единице, то значения пороговых уровней будут соответствовать выражению ±(2К - 1)α/2, где - [М/2] + 1 ≤ К ≤ [М/2]. Здесь [х] представляет собой целое число, ближайшее к х, но не превосходящее его. Тогда с учетом этого упрощения выражение (5.20) примет вид

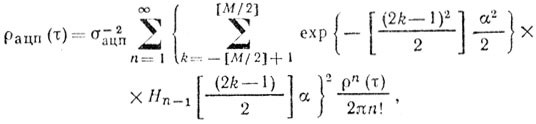(5.21)

где H_n(x) обладает следующими свойствами:

Функция Н_n(х) является четной для n четного и нечетной для n нечетного. Поскольку суммирование по k осуществляется от -[M/2] + 1 до [М/2], нет необходимости вычислять члены под знаком суммы, когда n - 1 нечетное, и следует учитывать только члены для положительных k, когда n - 1 четное. В результате выражение (5.21) сводится к следующему:

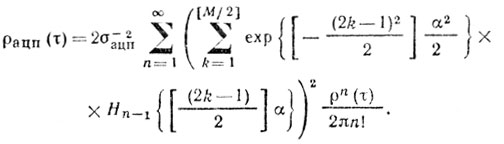(5.22)

Обозначим:

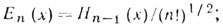
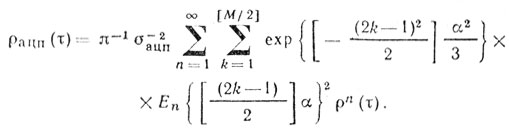(5.23)

Функция Е_n(х) удовлетворяет соотношениям:

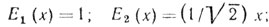
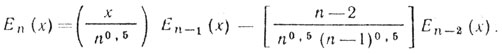
АЦП без нулевого выходного уровня (М-четное). АЦП с равномерным квантованием не имеет нулевого уровня выходного сигнала. Для этого случая ρ_ацп(τ), как следует из выражения (5.20), может быть приведен к виду, несколько отличному от (5.23). Снова пред положим, что α обозначает нормированное расстояние между порогами и размер шага равен единице. Пороги расположены на jα, где j - целые числа между - (М/2 - 1) и +(М/2 - 1), включая j = 0.

Тогда выражение (5.20) можно привести к виду

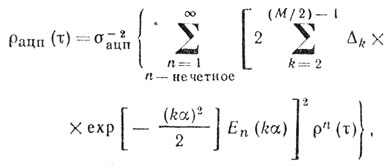(5.24)

где Δ_k = 1/2 при k = 0 и Δ_k = 1 при k ≠ 0.

В качестве примера использования полученных соотношений рассмотрим зависимость потерь квантования γ от параметра α для различного числа разрядов аналого-цифрового преобразования, а также различных значений коэффициента корреляции.

Коэффициент потерь для схемы однократной ЧПК

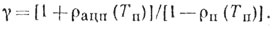(5.25)

На рис. 5.17 приведены графики потерь на аналого-цифровое преобразование для пяти- (а) и семиразрядного АЦП (б). Их них видно, что с увеличением разрядности преобразования потери значительно снижаются, а оптимальное значение α становится менее критичным к коэффициенту корреляции входного сигнала. Тем не менее в окрестности значений ρ(T_п), близких к единице, потери возрастают, что указывает на увеличение чувствительности системы СДЦ к изменению мощности пассивной помехи на входе АЦП. Поэтому при значительных колебаниях величины входного сигнала помехи (например, свыше 15-20 дБ) существенный выигрыш может дать адаптивная регулировка пороговых уровней в зависимости от интенсивности помехи.

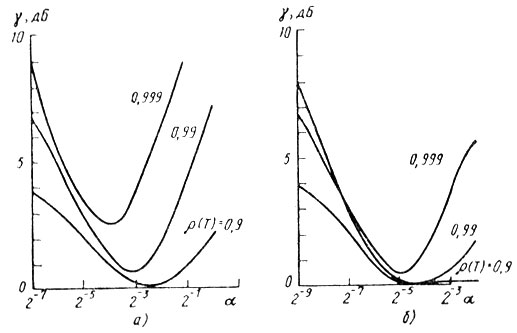
Рис. 5.17

Рассмотрим теперь характеристики схемы двухкратной ЧПВ, для которой коэффициент потерь

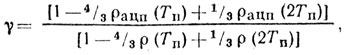(5.26)

где ρ_ацп(T_п) - нормированная функция корреляции помехи на выходе АЦП.

Для получения зависимости между γ, α и числом уровней квантования М необходимо определить взаимосвязь между ρ(T_п) и ρ(2T_п). Для энергетического спектра помехи, имеющего гауссовское распределение, функция корреляции имеет вид

где σ_τ = 1/2πσ²_fп.

Используя это выражение, получаем

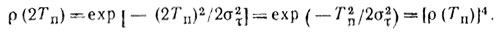(5.27)

На рис. 5.18 приведены зависимости влияния на коэффициент потерь γ величин α, ρ(T_п) и разрядности АЦП; а - для 5-разрядного АЦП, б - для 7-разрядного. По сравнению с однократной системой ЧПК потери значительно увеличились. Например, при ρ(T_п) = 0,99 потери составляют 14 дБ для 7-разрядного АЦП при оптимальном выборе шага квантования.

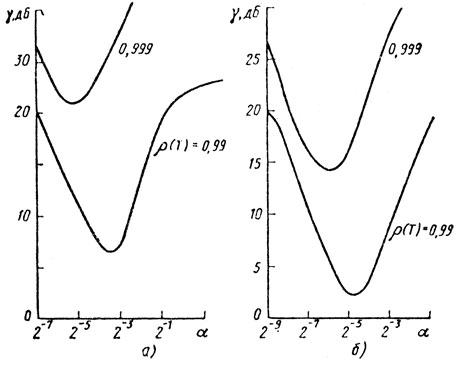
Рис. 5.18

При цифровой обработке смеси сигналов и пассивных помех из-за большого динамического диапазона обрабатываемых сигналов и малой длительности зондирующего импульса требуется использовать многоразрядные быстродействующие АЦП, что усложняет и удорожает систему подавления пассивных помех. В последнее время ведутся интенсивные работы по использованию РГФ, выполненных на приборах с зарядовой связью (ПЗС). В этих устройствах подавления осуществляется дискретизация сигналов только во времени, и поэтому их динамический диапазон легче согласуется с диапазоном принимаемых сигнала и помехи на входе системы подавления.

Особой разновидностью режекторных гребенчатых фильтров являются фильтровые системы, представляющие собой набор узкополосных доплеровских фильтров, включенных параллельно и образующих гребенчатые фильтры в каждом элементе дальности с помощью ключевых каскадов, отпираемых СИ.

Фильтровые системы подавления помех могут реализовываться как на аналоговых (электромеханических, пьезоэлектрических, магнитострикционных и других фильтрах), так и на цифровых элементах (цифровых фильтрах на БПФ или микропроцессорах). На рис. 5.19 [1] приведена типовая структурная схема фильтровой системы СДЦ, многоканальной по дальности (m каналов) и по скорости (n каналов). Селекторы дальности (СД) обеспечивают поступление в каждый канал дальности сигналов только с одного и того же элемента дальности. Узкополосные фильтры Ф₁, ..., Ф_n осуществляют селекцию по скорости в пределах диапазона доплеровских частот f_пч - f_пч + F_п/2, интеграторы (ИНТ) - накопление пачки импульсов после их детектирования амплитудным детектором (АД). Коммутатор объединяет каналы, позволяя проводить анализ сигналов после пороговых устройств (ПУ) в координатах R, υ_r. Отметим, что комбинация элементов СД, коммутируемого периодическими селекторными импульсами, и фильтров с полосой пропускания от f до f + Δf позволяет сформировать гребенчатую характеристику с периодом следования гребней F_п.

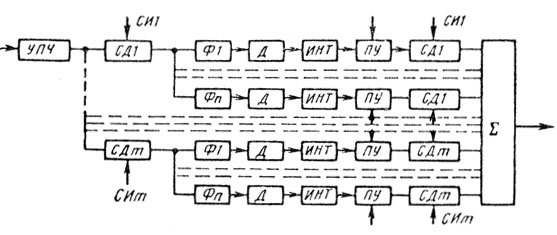
Рис. 5.19

На рис. 5.20 [8] приведена структурная схема цифровой фильтровой системы СДЦ с подавлением помех с помощью ЦРГФ, с последующей записью информации в оперативное ЗУ (ОЗУ) и n-точечным алгоритмом фильтрации на БПФ.

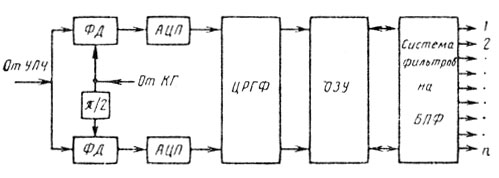
Рис. 5.20