
1.5. Радиоцепи и методы их анализа
Радиотехнические преобразования осуществляются с помощью большого числа линейных и нелинейных элементов и цепей. Линейные цепи, в свою очередь, подразделяются на цепи с постоянными и цепи с переменными параметрами. Последние часто называют параметрическими цепями.
Каждый из перечисленных классов цепей подразделяется, кроме того, на цепи с сосредоточенными и с распределенными параметрами. К первым относятся цепи, составленные из катушек индуктивности, конденсаторов и резисторов, а ко вторым - цепи, содержащие линии, волноводы, излучающие системы.
В данном курсе изучаются в основном цепи с сосредоточенными параметрами. Для выявления основных свойств указанных цепей необходимо напомнить свойства описывающих эти цепи дифференциальных уравнений. Имея в виду цепи с сосредоточенными параметрами, выпишем три следующих уравнения:
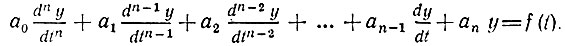 (1.1)
(1.1)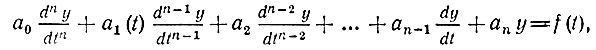 (1.2)
(1.2)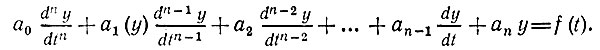 (1.3)
(1.3)Уравнение (1.1) - линейное, с постоянными коэффициентами а0, а1, а2, ... аn - характеризует линейную цепь с постоянными параметрами. Уравнение (1.2), в котором по крайней мере один из коэффициентов, (в данном случае а1(t)) является функцией времени (но не зависит от у), представляет собой линейное уравнение с переменным коэффициентом (или переменными коэффициентами) и описывает линейную цепь с переменными параметрами. Наконец, уравнение (1.3), один или несколько коэффициентов которого (в данном случае а1(у)) являются функциями у, представляет собой нелинейное дифференциальное уравнение, описывающее нелинейную цепь.
Обратимся сначала к свойствам линейного уравнения с постоянными коэффициентами. Для большей наглядности заменим общее уравнение (1.1) более простым уравнением второго порядка, описывающим, например, последовательный колебательный контур L, С, r, в который вводится э. д. с. е(t).
Для тока в контуре i(t) можно написать следующее интегродифференциальное уравнение:
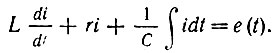 (1.4)
(1.4)Продифференцировав это уравнение по t и обозначив е'(t) = f (/), придем к уравнению типа (1.1).
Уравнение (1.4) является линейным, если коэффициенты L, r и 1/С не зависят от величины тока i или, что то же самое, от величины внешней силы е(t). При выполнении этого условия , напряжения на каждом из элементов контура линейно связаны с током. Действительно, обозначая эти напряжения соответственно через ur, uL и uс, можем написать
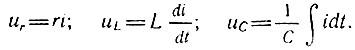 (1.5)
(1.5)Так как дифференцирование и интегрирование являются операциями линейными, можно утверждать, что uL и uС линейно связаны с током i при любом законе изменения последнего во времени. Относительно ur это утверждение еще более очевидно.
Одним из проявлений линейности цепи является независимость соотношения между входными и выходными напряжениями (токами) от уровня входного напряжения (тока).
В частности, при изменении тока по закону i = I sinωt получим
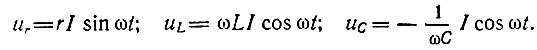 (1.6)
(1.6)Изменение амплитуды тока I в n раз дает такое же изменение амплитуды напряжения на элементах r, L и С. Это свойство линейных элементов можно толковать как результат линейности их вольт-амперных характеристик. Вольт-амперная характеристика для элемента r представлена на рис. 1.4, на котором по осям координат можно откладывать как мгновенные, так и амплитудные значения ur и i, а для элементов L и С - на рис. 1.5, где по осям отложены соответственно амплитуды UL, I или UC, I. Заметим, что вольт-амперные характеристики учитывают только связь между амплитудами UL, UC и I и не учитывают зависимость от частоты. Для элемента r функции i(t) и ur(t), как известно, могут отличаться только постоянным коэффициентом 1/r, который численно равен (см. рис. 1.4) угловому коэффициенту вольт-амперной характеристики:
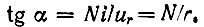
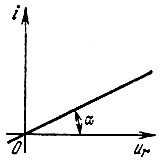
Рис. 14. Вольт-амперная характеристика линейного резистора
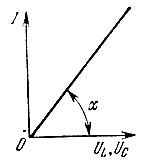
Рис. 1.5. Вольт-амперная (амплитудная) характеристика линейного элемента (L или С)
Для вольт-амперных характеристик I(UL) и I(UC), построенных при какой-либо фиксированной частоте ω, угловые коэффициенты
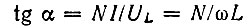
- для индуктивности и
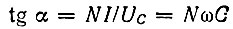
- для емкости.
В этих выражениях коэффициент N с размерностью сопротивления зависит от масштабов по осям абсцисс и ординат. Если напряжения, токи и сопротивления выражены соответственно в вольтах, амперах и омах, то N = 1 Ом.
Другим важным свойством линейных цепей, также вытекающим из линейности дифференциального уравнения, описывающего поведение (ток, напряжение) цепи, является справедливость принципа независимости или наложения (суперпозиции). Суть этого принципа может быть сформулирована следующим образом: при действии на линейную цепь нескольких внешних сил поведение цепи (ток, напряжение) можно определять путем наложения (суперпозиции) решений, найденных для каждой из сил в отдельности. Можно использовать еще и такую формулировку: в линейной цепи сумма эффектов от различных воздействий совпадает с эффектом от суммы воздействий. При этом предполагается, что цепь свободна от начальных запасов энергии.
Принцип наложения лежит в основе спектрального и операторного метода анализа переходных процессов в линейных цепях, а также метода интеграла наложения (интеграл Дюамеля). Применяя принцип наложения, любые сложные сигналы при передаче их через линейные цепи можно разложить на простые, более удобные для анализа (например, синусоидальные).
Остановимся еще на одном фундаментальном свойстве линейной цепи, прямо вытекающем из теории интегрирования линейных дифференциальных уравнений с постоянными коэффициентами. Разложив е(t) в правой части уравнения (1.4) с помощью ряда или интеграла Фурье на простейшие гармонические составляющие, действующие при -∞ < t < ∞, мы получим для каждой составляющей с частотой ωn решение уравнения (1,4) в виде гармонического колебания той же частоты:
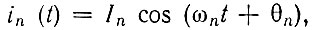
где In и θn - постоянные амплитуда и фаза.
Отсюда следует, что при любом сколь угодно сложном воздействии в линейной цепи с постоянными параметрами не возникает новых частот. Это означает, что ни одно из преобразований сигналов, сопровождающихся появлением новых частот (т. е. частот, отсутствующих в спектре входного сигнала), не может в принципе быть осуществлено с помощью линейной цепи с постоянными параметрами. Такие цепи находят широчайшее применение для решения задач, не связанных с трансформацией спектра, таких, как линейное усиление сигналов, фильтрация (по частотному признаку) и т. д.
Рассмотрим теперь свойства линейных цепей с переменными параметрами, вытекающие из свойств общего уравнения (1.2).
Как и в предыдущем случае, принцип наложения (суперпозиции) остается в силе. Это означает, что правую часть уравнения (1.2), т. е. внешнюю силу f(t), можно разложить на гармонические составляющие, действующие при -∞ < t < ∞, после чего решение уравнения (1.2) будет представляться в виде суммы независимых частных решений, соответствующих каждой из составляющих правой части. (Как и ранее, предполагается, что в цепи начальный запас энергии отсутствует.) Однако в отличие от предыдущего случая в цепи с переменными параметрами эти частные решения являются не гармоническими, а более сложными функциями. Иными словами, даже простейшее гармоническое воздействие создает в линейной цепи с переменными параметрами сложное колебание, имеющее спектр частот. Это можно пояснить на следующем простейшем примере. Пусть к резистору, сопротивление которого изменяется во времени по закону
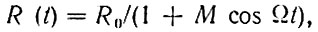
приложена гармоническая э. д. с.
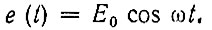
Ток через сопротивление
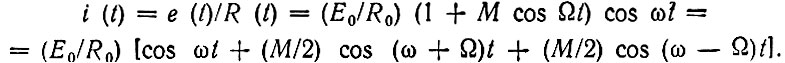 (1.7)
(1.7)Как видим, в составе тока имеются компоненты с частотами ω ± Ω, которых нет в е(t). Даже из этой простейшей модели ясно, что, изменяя во времени сопротивление, можно осуществить преобразование спектра входного сигнала.
Аналогичный результат, хотя и с более сложными математическими выкладками, можно получить для цепи с переменными параметрами., содержащей реактивные элементы - индуктивности и емкости. Этот вопрос рассматривается в гл. 10. Здесь лишь отметим, что линейная цепь с переменными параметрами преобразует частотный спектр воздействия и, следовательно, может быть использована для некоторых преобразований сигналов, сопровождающихся трансформацией спектра. Из дальнейшего будет также видно, что периодическое изменение во времени индуктивности или емкости колебательной цепи позволяет при некоторых условиях осуществить "накачку" энергии от вспомогательного устройства, изменяющего параметр ("параметрические усилители" и "параметрические генераторы", гл. 10).
Теория дифференциальных уравнений с переменными коэффициентами значительно более сложна, нежели уравнений с постоянными коэффициентами. Даже при гармонической правой части решение уравнений порядка выше первого можно найти лишь в некоторых частных случаях. Поэтому ясно, что, хотя к линейным цепям с переменными параметрами и применим принцип наложения, спектральный подход к анализу прохождения сигналов через такие цепи не всегда оказывается эффективным. Более подробно этот вопрос освещен в гл. 10.
Рассмотрим, наконец, общие свойства нелинейных цепей. Из теории нелинейных дифференциальных уравнений известно, что при решении этих уравнений принцип наложения неприменим. Это означает, что если уравнение типа (1.3) (для случая, например, n = 1) при правой части f1(t)
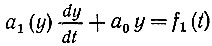
приводит к решению в виде функции у1(t), а аналогичное уравнение при правой части f2(t)
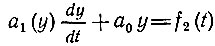
приводит к решению у2(t), то уравнение
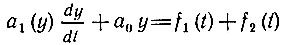
имеет своим решением функцию у3(t), которая не равна сумме y1(t) и y2(t):
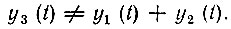
Таким образом, основным свойством нелинейных элементов и цепей является то, что для их анализа принцип наложения (суперпозиции) неприменим. Это свойство нелинейных цепей тесно связано с кривизной вольт-амперных (или иных аналогичных) характеристик нелинейных элементов (рис. 1.6). В отличие от вольт-амперной характеристики линейного резистора (рис. 1.4) в данном случае между током и напряжением нет прямой пропорциональности. Если напряжению u1 соответствует ток i1, а напряжению u2 - ток i2, то суммарному напряжению u3 = u1 + u2 будет соответствовать ток i3, отличный от суммы i1 + i2 (рис. 1.6).
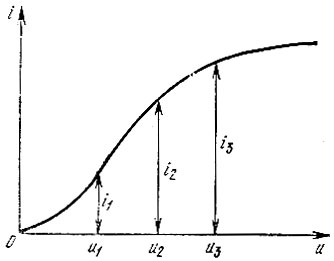
Рис. 1.6. Вольт-амперная характеристика нелинейного элемента (диода)
Из этого простого примера видно, что при анализе воздействия сложного сигнала на нелинейную цепь этот сигнал нельзя разлагать на более простые; необходимо искать отклик цепи на результирующий сигнал.
Неприменимость для нелинейных цепей принципа наложения делает непригодными спектральный и иные методы анализа, основанные на разложении сложного сигнала на составляющие.
Другим важным свойством нелинейной цепи является преобразование спектра сигнала. При воздействии на нелинейную цепь простейшего гармонического сигнала в цепи, помимо основной частоты, возникают гармоники с частотами, кратными основной частоте (а в некоторых случаях и постоянная составляющая тока или напряжения). В дальнейшем будет показано, что при сложной форме сигнала в нелинейной цепи, помимо гармоник, возникают еще и комбинационные частоты, являющиеся результатом взаимодействия отдельных частот, входящих в состав сигнала.
С точки зрения преобразования спектра сигнала следует подчеркнуть принципиальное различие между линейными параметрическими и нелинейными цепями. В нелинейной цепи структура спектра на выходе зависит не только от формы входного сигнала, но и от его амплитуды. В линейной параметрической цепи структура спектра от амплитуды сигнала не зависит.
Особенный интерес для радиотехники представляют свободные колебания в нелинейных цепях. Подобные колебания называются автоколебаниями, поскольку они возникают и могут устойчиво существовать в отсутствие внешнего периодического воздействия, Расход энергии при колебаниях в подобных цепях компенсируется источником энергии постоянного тока.
Основные радиотехнические процессы: генерация, модуляция, детектирование и преобразование частоты - сопровождаются трансформацией частотного спектра. Поэтому эти процессы можно осуществить с помощью либо нелинейных цепей, либо линейных, но с изменяющимися параметрами. В некоторых случаях используются одновременно как нелинейные, так и линейные параметрические цепи. Следует, кроме того, подчеркнуть, что нелинейные элементы работают в сочетании с линейными цепями, осуществляющими выделение полезных компонентов преобразованного спектра. В связи с этим деление цепей на линейные, нелинейные и параметрические является весьма условным. При анализе реальных радиотехнических цепей, содержащих нелинейные элементы, обычно для описания поведения различных узлов одного и того же устройства приходится применять разнообразные математические методы - линейные и нелинейные.
Следует, кроме того, отметить, что даже в пределах линейного рассмотрения цепи методы анализа зависят от типа линейной цепи - с сосредоточенными или с распределенными параметрами. Применение тех или иных цепей определяется рабочим диапазоном частот. Отсюда ясно, что полная классификация радиотехнических цепей не может быть проведена в отрыве от используемых диапазонов частот.

© RATELI.RU, 2010-2020
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
