9.9. Автогенератор с линией задержки в цепи обратной связи

Пусть имеется автогенератор с избирательной нагрузкой и линией задержки в кольце обратной связи. Подобный генератор можно представить в виде обобщенной схемы (рис. 9.23), аналогичной схеме на рис. 9.1. Рассматривая линию задержки как идеальный четырехполюсник с передаточной функцией е^-iωT, мы можем представить линейную часть схемы, состоящую из колебательного контура и задержки T, в виде одного четырехполюсника обратной связи с передаточной функцией

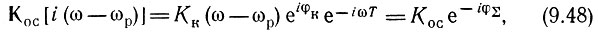
где К_к - модуль передаточной функции колебательного контура, обладающего резонансной частотой ω_р; φ_к - фазовая характеристика контура. В полосе прозрачности контура можно считать, что φ_к ≈ - (ω - ω_р) τ_к, где τ_к - постоянная времени контура.

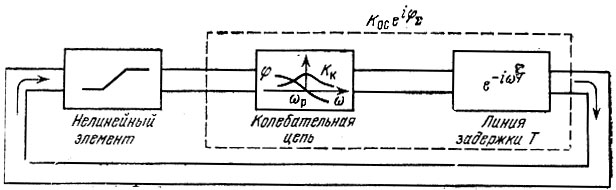
Рис. 9.23. Автогенератор с линией задержки в цепи обратной связи

Введение в схему линии задержки не изменяет модуля передаточной функции, но существенно влияет на результирующую фазовую характеристику

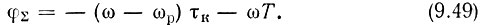
При достаточно большой задержке Т наклон результирующей фазовой характеристики определяется в основном слагаемым ωT, причем может оказаться, что в полосе прозрачности колебательной цепи изменение φ_Σ достигает значительной величины, превышающей несколько полных оборотов 2π. Подобный случай изображен на рис. 9.24, на котором ω_-2, ω_-1, ω₁, ω₂, ... обозначают частоты, лежащие в полосе прозрачности контура, при которых ординаты фазовой характеристики φ_Σ равны n2π, где n - целое число. Так как при указанных частотах выполняется баланс фаз и амплитуд (см. § 9.3), то каждая из них может являться частотой автогенерации. Введение в кольцо обратной связи достаточно большой задержки придает системе многочастотный характер. Роль колебательного контура при этом сводится лишь к ограничению числа частот, на которых обеспечивается усиление, необходимое для автогенерации.

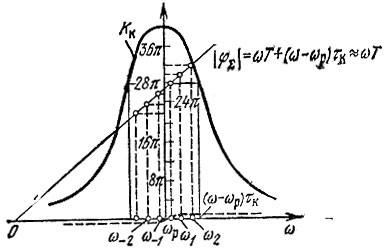
Рис. 9.24. Расположение возможных частот генерации при введении задержки в цепь обратной связи

Возникает вопрос, могут ли одновременно устойчиво существовать несколько автоколебаний с различными частотами. Ответ на него зависит от таких факторов, как число частот в полосе прозрачности контура, при которых выполняется фазовый баланс, форма амплитудно-частотной характеристики избирательной нагрузки, режим самовозбуждения (мягкий или жесткий) и некоторых других.

Рассмотрим сначала случай, когда в полосе прозрачности одиночного колебательного контура имеется всего лишь две частоты, на которых возможна генерация: ω₁ и ω₁. Это означает, что в полосе 2Δω₀ = 2/τ_к (τ_к - постоянная времени контура) набег фазы в линии задержки Т близок к 2π, т. е. 2Δω₀Т ≈ 2π или Т ≈ я/Δω₀ ≈ πτ_к.

Примерное расположение ω₁ и ω₂ на оси частот показано на рис. 9.25. Через Е₁ и Е₂ обозначены амплитуды колебаний с указанными частотами в какой-то момент времени после запуска генератора с мягким режимом возбуждения. При циклическом обходе замкнутого кольца обратной связи при каждом прохождении через нелинейный элемент соотношение между амплитудами Е₁ и Е₂ будет изменяться в пользу E₁. С аналогичной ситуацией мы имели дело при рассмотрении подавления слабого сигнала в амплитудном ограничителе в § 8.9. В итоге колебание с частотой ω₂ полностью подавляется и в системе остается всего лишь одно колебание с частотой ω₁, для которого начальные условия при запуске более благоприятны.

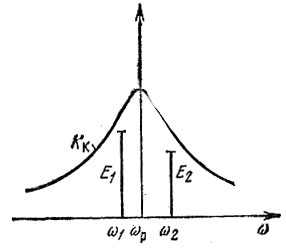
Рис. 9.25. К вопросу о подавлении слабого колебания в автогенераторе с задержкой в цепи обратной связи

Иначе обстоит дело в автогенераторе с жестким режимом самовозбуждения, когда при запуске для установления автоколебаний требуется посторонний источник колебаний. В зависимости от выбора запускающей частоты в генераторе может быть установлен стационарный режим на любой из частот: ω₁ или ω₂. Отсюда видно, что "жесткий" автогенератор с запаздывающей обратной связью можно использовать как устройство, запоминающее одну из нескольких частот, подаваемых в момент запуска.

Вернемся к автогенератору с мягким режимом самовозбуждения и допустим, что в полосе прозрачности колебательной цепи имеется значительное число частот возможной генерации. Так как эти частоты расположены на оси со эквидистантно (рис. 9.26), то можно допустить существование совокупности колебаний с частотами ω₁, ω₂, ω₃, ... при амплитудных и фазовых соотношениях, характерных для угловой модуляции. Подобное сложное колебание, обладающее постоянной амплитудой, проходит через нелинейность (амплитудный ограничитель) без деформации, т. е. без изменения соотношения между отдельными составляющими спектра. Это означает, что нелинейная часть автогенератора не препятствует одновременной генерации сетки частот. Этого, однако, еще недостаточно для устойчивой генерации. Необходимо, чтобы передаточная функция избирательной цепи обеспечивала сохранение внутриспектральных соотношений. Амплитудно-частотная характеристика избирательной цепи, представленная на рис. 9.26, не отвечает этому требованию. Более подробное рассмотрение [7] показывает, что для устойчивой генерации спектра частот амплитудно-частотная характеристика колебательной системы должна иметь неравномерность типа седловины (рис. 9.27).

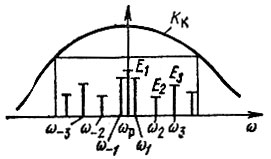
Рис. 9.26. Форма АЧХ избирательной цепи, неблагоприятная для одновременного генерирования нескольких частот

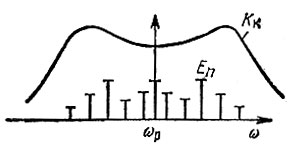
Рис. 9.27. Форма АЧХ избирательной цепи, допускающей устойчивую генерацию нескольких частот одновременно

Генератор с запаздывающей обратной связью обладает некоторыми другими интересными свойствами, обусловленными большой крутизной фазовой характеристики, например повышенной стабильностью генерируемой частоты.