9.11. Действие гармонической э. д. с. на автогенератор. Захватывание частоты

Поведение автогенератора, находящегося под действием внешней силы, существенно зависит от амплитуды и частоты этой силы.

Если амплитуда очень мала по сравнению с амплитудой автоколебания и одновременно частота ω значительно отличается от частоты ω_г = ω_р свободного автогенератора (ω_р - резонансная частота контура автогенератора), то действие внешней э. д. с. сводится к эффекту модуляции, который проявляется в изменении фазы и амплитуды автоколебания по весьма сложному закону. С приближением частоты ω к ω_р картина меняется. Частота генерации ω_г "подтягивается" к частоте со внешней э. д. с. и при некотором значении Δω = ω - ω_р, зависящем от соотношения амплитуд, автогенератор начинает работать точно на частоте ω_г = ω без каких либо признаков модуляции. Частота генератора оказывается "захваченной" или "увлеченной" частотой вынуждающей силы.

Явление захватывания частоты используется в ряде радиотехнических устройств, когда требуется осуществить принудительную синхронизацию автогенератора с помощью маломощного источника колебаний. В некоторых случаях, при наличии паразитных связей между двумя автогенераторами, явление захватывания возникает произвольно и препятствует независимой их работе на близких частотах.

Рассмотрим механизм явления захватывания частоты в простейшем одноконтурном автогенераторе с трансформаторной обратной связью при последовательном включении независимого источника э. д. с. в цепь база-эмиттер (рис. 9.30). Следует подчеркнуть, что такая схема выбрана только для определенности рассуждений. С точки же зрения установления общих соотношений вид схемы автогенератора и способ введения вынуждающей э. д. с. принципиального значения не имеют. Частоту генерации (в отсутствие внешней э. д. с.) приравняем резонансной частоте контура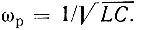

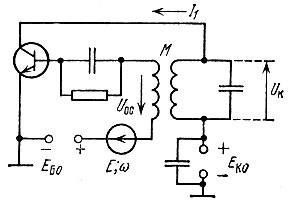
Рис. 9.30. Автогенератор с синхронизирующим источником э. д. с. в цепи база-эмиттер

Рассмотрим сначала баланс фаз в автогенераторе, находящемся под действием внешней э. д. с. е(t) = Е cos (ωt + θ₀), в предположении, что имеет место стационарный режим захватывания, т. е. генерируемая частота ω_г равна частоте ω, отличной от резонансной частоты контура ω_р. При этом амплитуду Е будем считать настолько малой, что все основные параметры автоколебания - амплитуда первой гармоники коллекторного тока I₁, амплитуда напряжения на контуре U_к и амплитуда напряжения обратной связи U_oc - останутся такими же, как и в отсутствие внешнего воздействия. Иными словами, влияние внешнего воздействия проявляется только в изменении фазовых соотношений в автогенераторе.

До включения источника внешней э. д. с. эти соотношения характеризуются векторной диаграммой, показанной на рис. 9.31, а. Ток I₁ в фазе с напряжением U_БЭ = U_oc, а напряжение U_к в фазе с током I₁ (напряжение на контуре отсчитывается от эмиттера к коллектору).

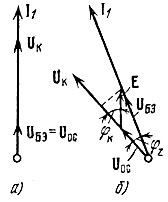
Рис. 9.31. Векторные диаграммы напряжений и тока в автогенераторе: а - без внешнего воздействия; б - в режиме захватывания частоты

Исходная фаза тока I₁ выбрана произвольно, так как в автогенераторе фаза автоколебания зависит от начальных условий запуска. После включения внешней э. д. с. е(t) = Е cos ωt (начальная фаза θ₀ приравнена нулю) и установления стационарного режима диаграмма примет вид, показанный на рис. 9.31, б. При построении этой диаграммы учтены следующие условия:

а) между током I₁ и напряжением U_к имеется фазовый сдвиг φ_z, зависящий от расстройки контура по отношению к генерируемой частоте ω. Принимая для определенности, что ω < ω_р, приходим к выводу, что вектор U_к должен опережать вектор I₁ на угол

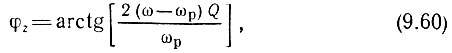
где Q - добротность контура;

б) ток I₁ находится в фазе с результирующим напряжением U_бэ;

в) напряжение обратной связи U_oc, связанное с напряжением контура U_к соотношением U_oc = MU_к/L, не зависит от частоты. Поэтому направления векторов U_oc и U_к совпадают.

Из диаграммы видно, что нарушение фазового баланса автогенератора в коллекторной цепи на угол φ_z (в сторону опережения) из-за расстройки колебательного контура (при ω < ω_р) компенсируется тем, что в цепи база-эмиттер результирующее напряжение U_бэ сдвинуто на угол φ_z, в сторону отставания относительно U_oc.

Когда ω > ω_р, фазовый сдвиг в коллекторной цепи является запаздывающим, а в цепи база-эмиттер - опережающим.

Из условий б) и в) а также непосредственно из диаграммы^* на рис. 9.31, б вытекает следующее равенство:

^* (Эту диаграмму удобно строить, исходя из произвольно выбранного положения вектор I₁, после чего вся диаграмма должна быть повернута на угол, при котором положение вектора Е соответствует заданной начальной фазе θ₀ внешней э. д. с.)

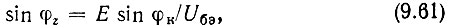
где φ_к - фазовый сдвиг между Е и U_к.

Итак, если режим захватывания действительно существует, то одновременно выполняются равенства (9.60) и (9.61).

Используя оговоренное условие малости Е по сравнению с U_ос, можно считать U_бэос,

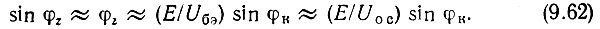
Малость угла φ_z позволяет также и в выражении (9.60) заменить тангенс его аргументом:

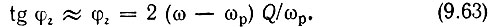
Приравнивая правые части последних двух выражений, приходим к следующему важному соотношению:

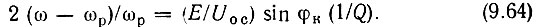
Из этого соотношения следует, что при заданной разности частот ω и ω_р сдвиг фазы напряжения U_к относительно синхронизирующего колебания равен

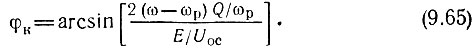
Соотношения (9.64) и (9.65) имеют смысл при условии, что абсолютная величина расстройки |ω - ω_р| не превышает некоторой предельной величины, при которой |sin φ_к| = 1. Из физических соображений очевидно, что эти предельные величины |ω - ω_р|_макс соответствуют границам полосы захватывания. Подставляя в уравнение (9.64) sin φ_к = ± 1, находим полную относительную ширину полосы захватывания в виде

Итак, полоса захватывания пропорциональна отношению амплитуды внешней э. д. с. к амплитуде колебаний свободного автогенератора и затуханию контура d = 1/Q.

В тех случаях, когда внешняя э. д. с. вводится непосредственно в колебательный контур автогенератора, выражению для полосы захватывания можно придать несколько иной вид. Рассмотрим в качестве примера схему генератора с контуром в цепи база-эмиттер (рис. 9.32). Схема эквивалентного контура, в котором действие обратной связи учтено генератором э. д. с. U_oc, изображена на рис. 9.33. В отсутствие постороннего воздействия амплитуда U_бэ связана с U_oc соотношением U_бэ = U_осQ.

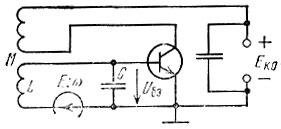
Рис. 9.32. Включение синхронизирующего источника э. д. с. в колебательный контур автогенератора

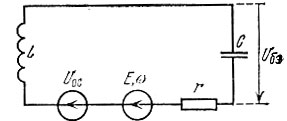
Рис. 9.33. Схема замещения контура к рис. 9.32

Подставляя это соотношение в формулу (9.66), получаем

Аналогично можно показать, что при введении вынуждающей э. д. с. в коллекторный колебательный контур получится соотношение

где U_к - амплитуда напряжения на контуре свободного автогенератора.

Нетрудно заметить, что отсутствие в формулах (9.67) и (9.68) величины Q объясняется тем, что постороннее воздействие оценивается э. д. с., вводимой последовательно в контур, а режим свободного автогенератора - напряжением, действующим на реактивном элементе контура. Если же оба напряжения определять одинаково: либо на реактивном элементе, либо как э. д. с., вводимую в контур последовательно, то независимо от схемы полосы захватывания будут определяться выражением вида (9.66).

Вне полосы захватывания частота генератора ω_г несколько отличается от частоты свободного автогенератора ω_р, и лишь при большой расстройке частот ω и ω_р можно считать ω_г → ω_р. Отклонение ω_г от ω_р возрастает, по мере приближения к границам области захватывания. Если, изменяя частоту со вынуждающей э. д. с. (при неизменной амплитуде), измерять частоту биений, то можно построить график, представленный на рис. 9.34, а сплошной линией. Штриховой линией показан ход изменения частоты биений при сложении колебаний от двух независимых источников: одного с частотой ω_г = ω_р = const и другого с изменяющейся частотой ω.

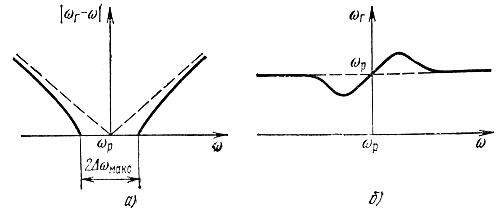
Рис. 9.34. Зависимости частоты биений |ω_г - ω| (а) и генерируемой частоты ω_г (б) от частоты синхронизирующего источника

То обстоятельство, что сплошная линия идет ниже штриховой, объясняется уже отмеченным в начале данного параграфа фактом "подтягивания" частоты автогенератора ω_г к частоте внешней э. д. с. ω. В полосе захватывания, где частота ω_г полностью совпадает с частотой ω, биения отсутствуют.

График зависимости генерируемой частоты ω_г от частоты со вынуждающей э. д. с. представлен (в ином масштабе частот) на рис. 9.34, б.