10.11. Свободные колебания в контуре с периодически изменяющейся емкостью

Составим уравнение для колебательного контура, емкость которого изменяется по закону

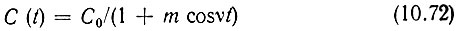
при L = const, r = const, а внешнее воздействие отсутствует:

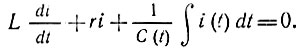
Переходя от тока i к заряду q и учитывая выражение (10.72), получаем

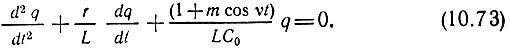
Величина 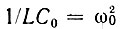определяет резонансную частоту контура в отсутствие модуляции емкости, т. е. при m = 0.

Таким образом, уравнение (10.73) можно записать в форме

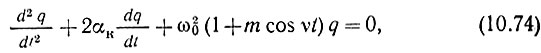
где использовано обозначение α_к = r/2L.

Для приведения уравнения (10.74) к канонической форме используется подстановка

исключающая из уравнения (10.74) первую производную q.

Дифференцируя дважды выражение (10.75):

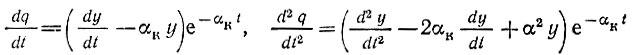
и подставляя полученные результаты в уравнение (10.74), получаем

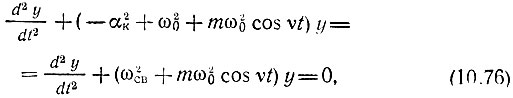
где 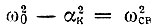есть квадрат частоты свободных колебаний контура (в отсутствие модуляции емкости).

Переходя к безразмерному времени

и вводя обозначения

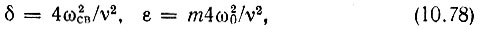
перепишем последнее уравнение в форме

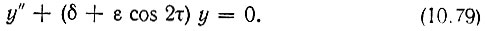
Это уравнение называется уравнением Матье. Теория уравнения Матье хорошо разработана. Каждому значению параметра ε соответствует последовательность определенных значений δ, при которых решениями уравнения (10.79) являются периодические функции Матье, обладающие периодом 2π относительно переменной τ.

Зависимость между значениями ε и δ, при которых существуют периодические решения уравнения (10.79), представлена кривыми на рис. 10.25. При больших значениях ε функции Матье имеют весьма сложную форму. При ε << 1 эти функции по форме мало отличаются от гармонических колебаний. При ε → 0 уравнения (10.76) и (10.79) переходят соответственно в уравнения

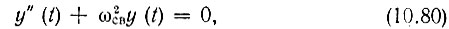
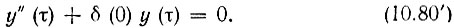
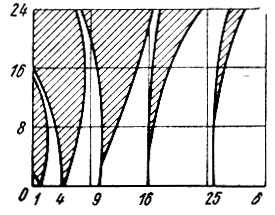
Рис. 10.25. Зоны устойчивости (не заштрихованы) и неустойчивости (заштрихованы) решений уравнения Матье

Уравнению (10.80) соответствуют решения в виде гармонических колебаний cos ω_свt и sin ω_свt, а уравнению (10.80') - соответственно 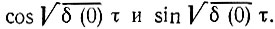Для того чтобы последние два решения могли являться периодическими функциями Матье с периодом 2π относительно переменной τ, т. е. чтобы они имели вид cos nτ или sin nτ, где n - целое число, величина δ(0) должна равняться квадрату целого числа n. Отсюда следует, что представленные на рис. 10.25 графики при ε = 0 должны касаться оси абсцисс в точках δ(0) = n = 1, 4, 9, ...

При произвольных значениях ε и δ общее решение уравнения Матье имеет вид

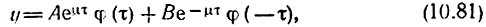
где А и В - постоянные, зависящие от начальных условий; φ(τ) - периодическая функция Матье, зависящая от параметра ε; μ - показатель, зависящий от параметров ε и δ исходного уравнения (10.79).

Для параметрических цепей, используемых в высокочастотной технике, характерен режим неглубокой модуляции емкости (или индуктивности). Обычно коэффициент модуляции m измеряется единицами процентов, так что и параметр ε, определяемый формулой (10.78), мал по сравнению с единицей. Поэтому, основываясь на отмеченных выше свойствах функций Матье, при ε << 1, можно записать общее решение в форме

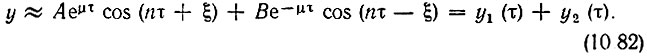
Для дальнейшего рассмотрения необходимо установить связь между показателем μ и параметрами ε, δ, а также определить фазу ξ.

Для этого в исходное уравнение (10.79) подставим одно из частных решений, например y₁(τ). Для упрощения анализа положим n = 1, т. е. ограничимся исследованием зависимости μ от ε, δ в области значений δ, близких к единице. Таким образом,

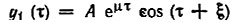
Сгруппировав после подстановки в (10.79) слагаемые, содержащие множители cos τ и sin τ, придем к следующему уравнению^*:

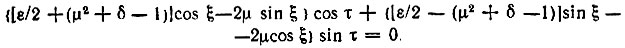
^* (Слагаемые вида cos 3τ и sin 3τ опущены.)

Так как это равенство должно выполняться при любых значениях τ, коэффициенты при cos τ и sin τ можно приравнять нулю.

Таким образом, получаем два уравнения для определения μ и ξ:

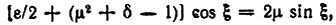
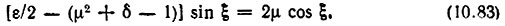
Из первого уравнения следует, что

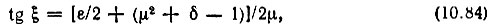
а из второго -

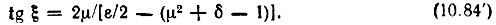
Приравнивая правые части выражений (10.84) и (10.84'), получаем

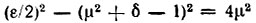
или

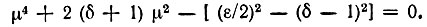
Отсюда следует, что

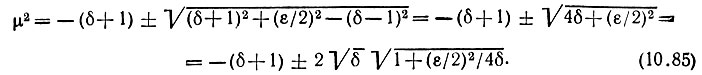
Из этого выражения видно, что μ² - вещественное число. Следовательно, показатель μ может быть либо вещественной (положительной или отрицательной), либо чисто мнимой величиной.

Если μ - вещественное число, положительное или отрицательное, то решение уравнения Матье неустойчиво, так как одно из слагаемых выражения (10.82) с увеличением τ неограниченно возрастает. При мнимых значениях μ решение устойчиво.

Случай неустойчивости соответствует таким значениям δ и ε, при которых изображающая их точка на рис. 10.25 находится в одной из заштрихованных зон. Показанные на этом рисунке кривые представляют собой границы, отделяющие зоны устойчивости от зон неустойчивости. Сплошные кривые на рис. 10.25 являются геометрическим местом точек, удовлетворяющих условию μ = 0. При этом, как отмечалось выше и как вытекает из выражения (10.82), решения уравнения Матье являются периодическими функциями. Физический смысл неустойчивого решения заключается в том, что при определенных соотношениях между глубиной модуляции емкости и относительной частотой этой модуляции (ε и δ) при любых сколь угодно малых начальных возмущениях (например, тепловые шумы) в контуре возникают колебания с неограниченно нарастающей амплитудой. Источником энергии для этих колебаний служит генератор накачки, воздействующий на емкость.

Отдельные неустойчивые области достигают оси абсцисс в точках δ = n², где n = 2ω_св/ν = 1, 2, 3, ... Это означает что при δ = 1, 4, 9, ..., т. е. при ν = 2μ_св, ν = μ_св, ν = ²/₃μ_св, ν = ¹/₂μ_св и т. д., решения уравнения Матье неустойчивы при сколь угодно малой глубине модуляции параметра m (ε → 0). При промежуточных значениях ν, когда воздействие на параметр производится не в такт с собственной частотой контура, для неустойчивости требуется тем большее значение ε, чем ниже частота ν.

В области малых значений ε выражение (10.85) можно упростить [например, при выборе знака плюс перед последним слагаемым в правой части (10.85)]:

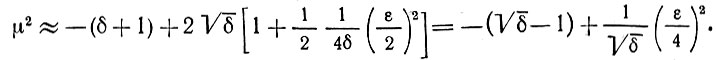
Таким образом,

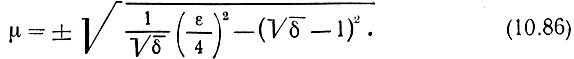
Обратимся вновь к общему решению (10.82) и перейдем от y к q [по формуле (10.75),] а также от τ к размерному времени t [по формуле (10.77)]:

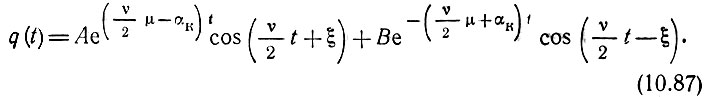
Из этого выражения видно, что для неустойчивости системы (по отношению к q) необходимо, чтобы μ было не только вещественным числом, но и превышало по абсолютной величине отношение 2α_к/ν.

Итак, критическое значение показателя μ, соответствующее границе между устойчивым и неустойчивым состояниями системы, определяется равенством

Подставив это значение μ в формулу (10.86), находим критическое значение

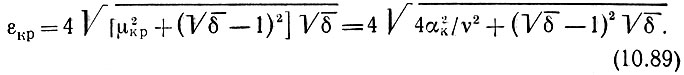
Но в соответствии с (10.78)

Отсюда находим m_кр - критическое значение глубины модуляции емкости (на грани возникновения генерации)

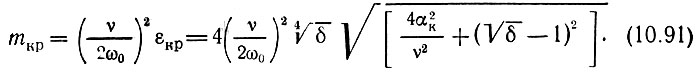
В частном случае 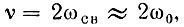когда δ = 1, получаем

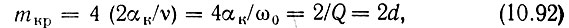
где Q = 1/d - добротность контура.

Этот результат совпадает с условием (10.65), полученным из рассмотрения стационарного режима параметрического усилителя.

Если частота ν модуляции емкости превышает частоту ω_св не точно вдвое (имеется расстройка)

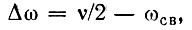
то неустойчивость системы возникает при больших значениях m_кр, чем 2/Q.

В этом случае

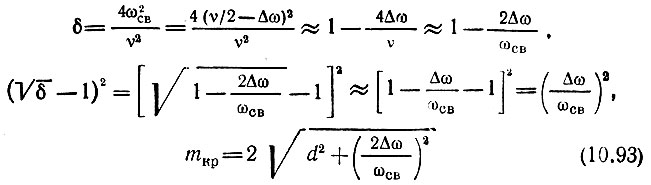
или

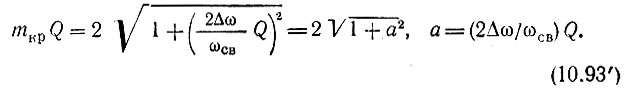
График зависимости m_крQ от а изображен на рис. 10.26 (сплошная кривая). Двойной штриховкой обозначена область возбуждения колебаний (при m > m_кр), а горизонтальной - область неустойчивых решений уравнения Матье, которые, однако, после умножения на е^-α_кt приводятся к устойчивым решениям. Наконец, незаштрихованная область соответствует устойчивым решениям уравнения Матье и тем более устойчивым решениям уравнения (10.74). Рис. 10.26 по существу является изображением в увеличенном масштабе одного "языка" диаграммы рис. 10.25 в окрестности точек δ = 1, ε = 0. На основании проведенного рассмотрения нетрудно определить все параметры свободного колебания в параметрическом контуре.

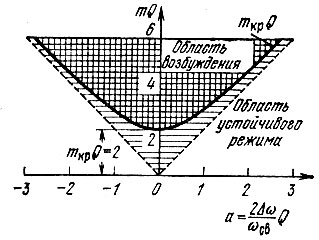
Рис. 10.26. Зоны устойчивости и неустойчивости решений уравнения Матье в окрестности точки δ = 1, ε = 0

Пусть в момент t = 0 начинается процесс периодической модуляции емкости по закону (10.72), причем соотношение параметров m, ν, ω_св и Q таково, что система неустойчива вблизи δ = 1.

Определив по формуле (10.86) величину |μ| и подставив ее в (10.84), найдем фазу ξ. В частности, при δ = 1, когда |μ| = ε/4,

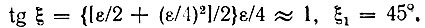
Тогда общее решение (10.87) примет следующий вид:

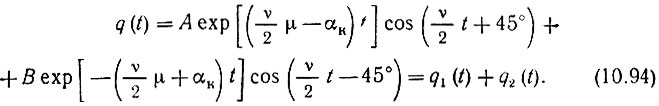
На рис. 10.27 изображены графики C(t) = С₀/[1 + m cos νt] а также cos (νt/2 + 45°) и cos (νt/2 - 45°). (В данном случае ν/2 = ω_св.) Последние два графика характеризуют изменение зарядов q₁(t) и q₂(t). Из этого рисунка видно, что убывание емкости соответствует прохождению q₁ через амплитудные, а q₂ - через нулевое значения. Это означает, что q₁(t) "правильно" сфазировано относительно закона изменения С(t) и накачка приводит к росту амплитуды (по закону exp [(μν/2 - α_к) t], а q₂(t) сфазировано неправильно: в моменты амплитудных значений заряда емкость растет, что приводит к отбору энергии из контура и к затуханию амплитуды (по закону ехр [-(μν/2 + α_к) t]).

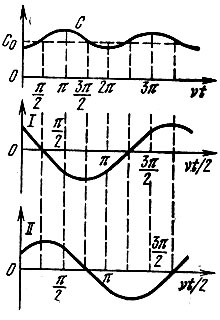
Рис. 10.27. Модуляция емкости и законы изменения заряда, обеспечивающие (график I) или не обеспечивающие (график II) параметрическое возбуждение колебания

На основании приведенных рассуждений можно наметить следующую картину возникновения и нарастания колебаний в параметрическом контуре. В момент включения контура (или в момент запуска генератора накачки) в нем существуют беспорядочные шумовые колебания, вызываемые тепловым движением заряженных частиц.

В составе этих колебаний имеется и компонент с частотой однако амплитуда и фаза этого компонента являются случайными величинами. Допустим, что в рассматриваемый начальный момент времени интересующий нас компонент имеет амплитуду ОА и фазу θ (рис. 10.28). Разложим вектор, изображающий это колебание, по двум взаимно перпендикулярным направлениям: N₁N₂ и М₁М₂. Прямая N₁N₂ проведена к оси абсцисс под углом ξ₁ = 45°, а прямая М₁М₂ - под углом ξ₂ = -45°. Вектор OD, совпадающий с прямой N₁N₂ и равный ОА cos (θ - ξ), изображает колебание, правильно сфазированное относительно фазы напряжения накачки, а вектор ОС, совпадающий с прямой М₁М₂, изображает колебание, которое под воздействием изменения емкости начинает затухать. Можно поэтому считать, что начальные условия для параметрического контура определяются той составляющей, фаза которой согласована с фазой напряжения накачки. Таких положений вектора существует два: при ξ₁ = 45° и ξ₁ = 225° (для частного случая ν = 2ω_св). Если вектор ОА расположен над прямой М₁М₂, то проекция его на прямую N₁N₂ положительна, в противном случае - отрицательна. Это означает, что при заданной фазе напряжения накачки фаза колебания в параметрическом контуре может принимать одно из двух фиксированных значений, различающихся на 180°.

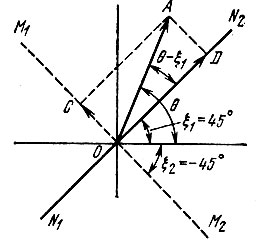
Рис. 10.28. Влияние начальных условий на установление режима параметрической генерации

Отметим в заключение, что основные результаты данного параграфа можно распространить на контур, в котором периодически изменяющимся элементом является индуктивность.