4.5. Точность амплитудных методов радиопеленгации

Перейдем теперь к оценке точности амплитудных методов радиопеленгации.

При пеленгации по методу максимума ошибка пеленга возникает из-за неточного определения момента, когда амплитуда пеленгуемого сигнала достигает максимума. Действительно, если оператор за максимальное значение амплитуды сигнала вместо U₀ примет U (рис. 4.8), то возникнет ошибка пеленга Δα. Эту ошибку можно найти следующим путем.

Относительная ошибка определения максимума пеленгуемого сигнала может быть представлена как

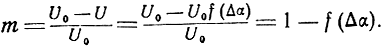
Разложим функцию f(Δα) в ряд Маклорена

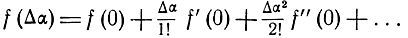
Ограничиваясь, в силу малости Δα, тремя первыми членами разложения и учитывая, что f(0) = 1, а f'(0) = 0, получим

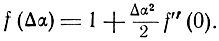
Тогда

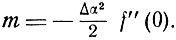
Откуда

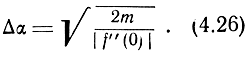
Из полученного выражения видно, что точность пеленгации методом максимума зависит от точности определения максимума амплитуды пеленгуемого сигнала и кривизны пеленгационной характеристики в направлении максимума.

Точность определения максимума пеленгуемого сигнала зависит, главным образом, от отношения сигнал/помеха, типа индикатора и характера флюктуаций отраженного сигнала. При хорошей различимости сигнала среднеквадратичное значение m ориентировочно равно

Кривизна пеленгационной характеристики в направлении максимума зависит от ширины пеленгационной характеристики, которая, в свою очередь, зависит от ширины диаграммы направленности антенны и от того, используются ли при пеленгации направленные свойства только приемной антенны, или приемной и передающей антенн одновременно.

Ориентировочно можно считать, что при хорошей различимости сигнала средняя квадратическая ошибка пеленга равна

Рассмотрим теперь ошибки, возникающие при пеленгации по методу минимума.

В силу того, что на входе приемника всегда имеется напряжение помех, принимаемый сигнал не будет наблюдаться не только в направлении нулевого приема, но и в пределах угла 2ψ (рис. 4.20) около этого направления. Этот угол в слуховых радиопеленгаторах принято называть углом молчания. Величина угла, в пределах которого сигнал отсутствует, может быть найдена следующим путем.

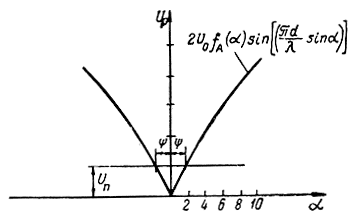
Рис. 4.20. Угол отсутствия сигнала при пеленгации по методу минимума

При противофазном включении двух приемных антенн согласно формуле (4.23)

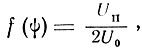
где U_п - среднеквадратичное значение напряжения помех.

Разложим функцию f(ψ) в ряд Маклорена

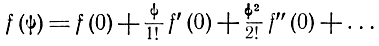
При малых значениях ψ можно ограничиться двумя первыми членами разложения. Учитывая, что f(0) = 0, получаем

Тогда

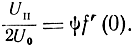
Откуда

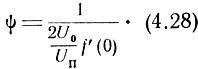
Средняя квадратическая ошибка пеленга будет составлять какую-то часть от угла ψ, т. е.

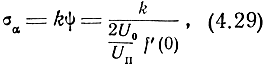
где k - коэффициент пропорциональности.

Ориентировочно можно принять k = 0,2÷0,5.

Из выражения (4.29) следует, что точность пеленгации методом минимума зависит от отношения сигнал/помеха и крутизны пеленгационной характеристики в направлении минимума.

Крутизна пеленгационной характеристики в направлении минимума, как следует из формулы (4.23), равна

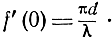
Как видим, крутизна пеленгационной характеристики в направлении минимума зависит от отношения ^d/_λ и не зависит от направленных свойств антенн. Для повышения крутизны пеленгационной характеристики, а следовательно, и точности пеленгации необходимо отношение ^d/_λ увеличивать. Однако при 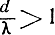пеленгационная характеристика будет иметь несколько направлений нулевого приема, что, естественно, вызывает неоднозначность пеленгации. Для иллюстрации сказанного на рис. 4.21 представлена пеленгационная характеристика при f_а(α) = const и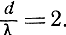

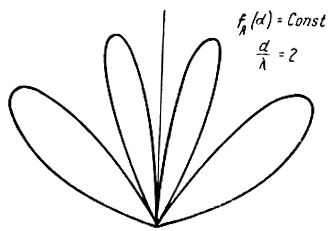
Рис. 4.21. Пеленгационная характеристика при противофазном включении двух антенн (^d/_λ = 2)

Неоднозначность пеленгации можно устранить путем применения направленных антенн, ширина диаграммы направленности которых не превышает ширины зоны однозначного пеленгования.

Следует заметить, что при большом отношении сигнал/помеха можно получить приемлемую точность пеленгации даже при широких пеленгационных характеристиках. Поэтому пеленгация методом минимума находит широкое применение в радионавигации, где большие значения отношения сигнал/помеха не являются исключением. Однако в радиолокации, наоборот, напряжение сигнала обычно незначительно превышает напряжение шума. Поэтому применение широких пеленгационных характеристик не обеспечивает приемлемой точности.

Все сказанное о точности метода минимума относится к случаю, когда две противофазно включенные антенны работают только как приемные. Аналогичным путем может быть определена точность и в случае, когда обе антенны используются и как приемные, и как передающие. Заметим, что при прочих равных условиях точность пеленгации во втором случае будет хуже, чем в первом.

Перейдем теперь к рассмотрению точности равносигнального метода пеленгации.

При этом методе ошибки пеленга возникают из-за неточного определения момента, когда амплитуды сигналов, соответствующие двум пересекающимся пеленгационным характеристикам, равны между собой.

Если оператор будет считать сигналы U₁ и U₂ равными, то возникает ошибка пеленга, которая может быть найдена следующим путем.

Коэффициент амплитудной модуляции, вызванной смещением пеленгационных характеристик, можно представить как

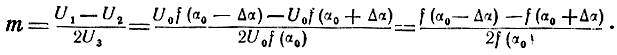
Разложим функции f(α₀ + Δα) и f(α₀ - Δα) в ряд Тейлора

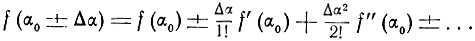
При малых значениях Δα можно ограничиться двумя первыми членами разложения.

Тогда

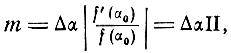
откуда

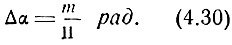
Отношение

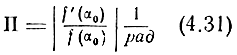
условимся называть пеленгационной способностью.

Подставив в формулу (4.30) вместо m среднеквадратическое значение минимального, т. е. порогового, коэффициента модуляции, получим среднюю квадратическую ошибку пеленга

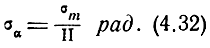
Из выражения (4.32) следует, что точность пеленгации при равносигнальном методе зависит от порогового коэффициента модуляции и пеленгационной способности. Пороговый коэффициент модуляции, в свою очередь, зависит, главным образом, от отношения сигнал/помеха, типа выходного устройства и величины флюктуаций отраженного сигнала. При хорошей различимости сигнала ориентировочно можно принять σ_m = 0,02.

Пеленгационная способность зависит от параметров антенной системы. Эта зависимость будет рассмотрена в следующем параграфе.

Точность пеленгации методом сравнения может быть определена аналогичным путем.

Следует иметь в виду, что приведенный анализ точности амплитудных методов радиопеленгации носит приближенный характер. Однако более строгий и точный анализ точности не меняет ни полученных выводов, ни порядка приведенных величин.