§ 1.6. Отражение плоских радиоволн на границе раздела двух сред

Реальные источники создают сферические волны, но на большом расстоянии от источника малую часть фронта сферической волны можно считать плоской. Сферическую поверхность на небольшом участке тоже можно считать плоской. Поэтому наиболее простой случай отражения плоской волны от плоской границы раздела двух сред представляет практический интерес.

Электромагнитная волна, падая на границу раздела двух сред, частично отражается от нее, частично проходит в глубь второй среды. Поэтому в первой среде имеются падающая и отраженная волны, а во второй среде - преломленная волна. Часто бывает необходимо знать соотношение между составляющими поля E и H падающей и отраженной волн, например, при распространении радиоволн вблизи поверхности Земли.

Отражение радиоволн на границе раздела двух идеальных диэлектриков

При идеально ровной поверхности, согласно закону геометрической оптики, угол отражения равен углу падения θ, а угол преломления ψ связан с углом падения соотношением [1]

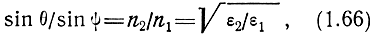
где ε₁ и ε₂ - соответственно относительные диэлектрические проницаемости первой и второй среды.

Рассмотрим отдельно отражение вертикально- и горизонтально-поляризованных волн и найдем отношение комплексных амплитуд напряженностей электрического поля падающей E^⋅_m и отраженной E^⋅_1m волн, называемое коэффициентом отражения:

Вертикальная поляризация. На рис. 1.10 изображено отражение вертикально-поляризованной волны от границы раздела двух сред.

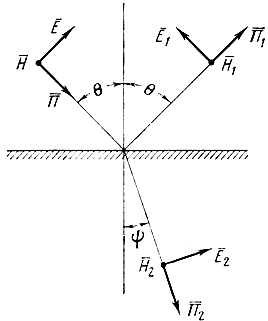
Рис. 1.10. Отражение вертикально-поляризованной волны от границы раздела двух сред

На границе раздела двух сред выполняются условия равенства тангенциальных составляющих векторов Е‾ и Н‾ [1]. На основании этого граничного условия можно составить следующие уравнения (см. рис. 1.10):

Воспользовавшись соотношением между величинами E^⋅ и Н^⋅ [см. формулу (1.32)] и выразив угол ψ через угол θ, после преобразований получим

Проследим зависимость коэффициента отражения от угла падения волны на границу раздела двух сред для случаев, когда первая среда обладает меньшей или большей диэлектрической проницаемостью, чем вторая.

В первом случае (ε₁ < ε₂) коэффициент отражения меняется от правильной положительной дроби (|R_в| < 1, Ф_в = 0) при θ = 0 до R_в = -1 при θ = 90°. Отрицательное значение коэффициента отражения можно интерпретировать, как изменение фазы коэффициента отражения Ф_в (а следовательно, и фазы отраженной волны) на 180°. Рассматриваемые зависимости модуля и фазы коэффициента отражения изображены на рис. 1.11 сплошными линиями.

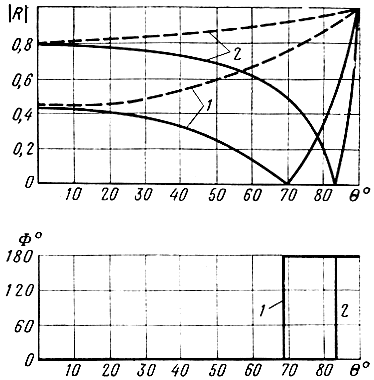
Рис. 1.11. Зависимости модуля и фазы коэффициента отражения от угла падения волны на границу раздела двух идеальных диэлектриков, когда ε₁ < ε₂: 1 - ε₁ = 1, ε₂ = 10; 2 - ε₁ = 1, ε₂ = 80; ^____ вертикальная поляризация; - - - горизонтальная поляризация

Из графиков видно, что при некотором значении угла θ = θ₀ отраженная волна отсутствует. При этом вся энергия падающей волны переходит во вторую среду. Угол θ₀ называется углом полного преломления. Величину угла θ₀ легко определить, приравняв числитель выражения (1.69) нулю, откуда

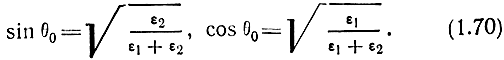
Во втором случае (ε₁ > ε₂) коэффициент отражения меняется от правильной отрицательной дроби (|R_в| < 1, Ф_в = 180°) при θ = 0 до |R_в| = 0 при θ = θ₀, где θ₀ определяется формулой (1.70). С дальнейшим увеличением угла модуль коэффициента отражения возрастает и при некотором значении θ = θ_кр, называемом критическим углом, становится равным единице.

Значение угла θ_кр определяется выражением

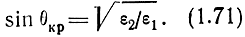
При θ > θ_кр вторые слагаемые в числителе и знаменателе уравнения (1.69) становятся мнимыми величинами, модуль коэффициента отражения остается равным единице, а фаза коэффициента отражения меняется от 0 до 180°. Явление, когда коэффициент отражения остается равным единице, называется полным внутренним отражением. Оно наблюдается, например, при отражении радиоволн от слоев ионосферы. Зависимость модуля и фазы коэффициента отражения от угла падения волны на границу раздела двух сред в этом случае изображена на рис. 1.12 сплошными линиями.

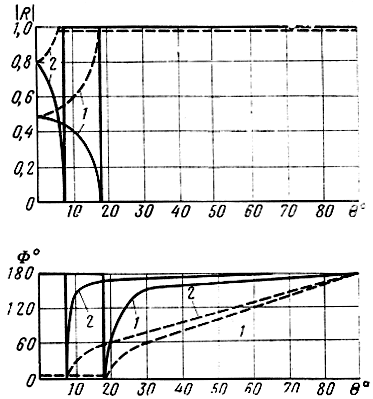
Рис. 1.12. Зависимости модуля и фазы коэффициента отражения от угла падения волны на границу раздела двух идеальных диэлектриков, когда ε₁ > ε₂: 1 - ε₁ = 10, ε₂ = 10; ε₂ = 1; 2 - ε₁ = 80, ε₂ = 1; ^____ вертикальная поляризация; - - - горизонтальная поляризация

Горизонтальная поляризация. В случае горизонтальной поляризации граничные условия согласно рис. 1.13 запишутся так:

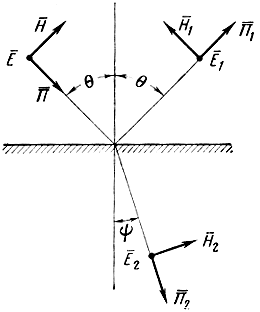
Рис. 1.13. Отражение горизонтально-поляризованной волны от границы раздела двух сред

Используя соотношение (1.32) и проводя преобразования, получим выражение для коэффициента отражения горизонтально-поляризованной волны:

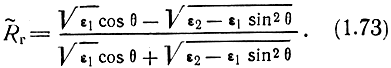
При горизонтальной поляризации зависимость коэффициента отражения от угла падения волны на границу раздела двух сред иная, чем при вертикальной поляризации.

Из анализа выражения (1.73) следует, что при ε₂ > ε₁ модуль коэффициента отражения меняется от правильной дроби при θ = 0 до |R_г| = 1 при θ = 90°; фаза коэффициента отражения Ф_г остается все время равной 180°. Эта зависимость изображена на рис. 1.11 пунктирными линиями.

Пои ε₂ < ε₁ модуль |R_г| меняется от некоторой дроби при θ = 0 до |R_г| = 1 при θ = θ_кр. Угол θ_кр определяется так же, как в случае вертикальной поляризации (1.71), и при дальнейшем увеличении угла θ модуль |R_г| остается равным единице, а фаза изменяется от 0 до 180°. Эта зависимость изображена на рис. 1.12 пунктирными линиями.

Таким образом, явление полного отражения наблюдается как при горизонтальной, так и при вертикальной поляризации, если волна падает из более плотной среды в менее плотную.

Явление полного преломления не имеет места в случае горизонтальной поляризации. Это можно объяснить тем, что при прохождении волны во второй среде находящиеся в ней заряды колеблются в направлении вектора Е‾ этой волны (рис. 1.14).

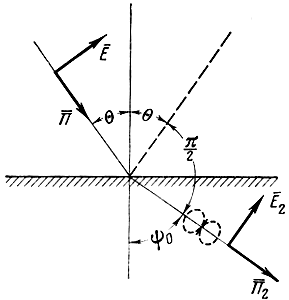
Рис. 1.14. К пояснению явления полного преломления

Колеблющиеся заряды излучают, как элементарные электрические вибраторы, т. е. не излучают вдоль своей оси. Из (1.70) следует, что в случае вертикальной поляризации при θ = θ₀ направление ориентации осей вибраторов совпадает с направлением, в котором должна была бы распространяться отраженная волна.

Синус угла преломления оказывается при этом равным косинусу угла падения:

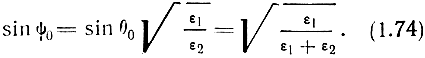
Следовательно, θ₀ + ψ₀ = 90° и в направлении 0О излучение отсутствует.

В случае горизонтальной поляризации вектор Е‾ при всех углах падения волны направлен параллельно границе раздела и нормально к плоскости падения волны. Поэтому направление ориентации осей вибраторов не может совпасть с направлением отраженной волны, и отраженная волна всегда существует.

Отражение радиоволн на границе раздела полупроводящих сред

Выражение для коэффициентов отражения радиоволн от полупроводящих сред получим путем замены в формулах (1.69) и (1.73) величины ε на комплексную величину ε˜. Величины R_в И R_г в этом случае являются также комплексными и их можно записать в виде

где Ф_в и Ф_г могут быть отличны от 0 и 180°.

При отражении от полупроводящей среды модуль и фаза коэффициента отражения зависит от частоты, так как величина ε˜ тоже зависит от частоты.

На рис. 1.15 представлены зависимости модуля и фазы коэффициента отражения, рассчитанные для случаев падения волн различной длины из среды с ε₁ = 1, γ = 0 на полу проводящую поверхность, для которой ε₂ > 1, γ ≠ 0. Сплошные кривые относятся к вертикальной, пунктирные - к горизонтальной поляризации.

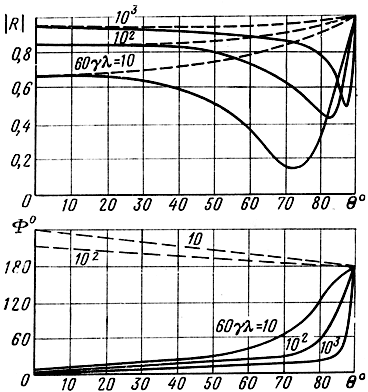
Рис. 1.15. Зависимости модуля и фазы коэффициента отражения от угла падения волны на границу раздела среды воздух - почва, когда ε₁ = 1, ε₂ = 10: ^___ вертикальная поляризация; - - - горизонтальная поляризация

Из графиков видно, что для вертикальной поляризации характерно наличие минимума модуля коэффициента отражения, явления полного преломления в чистом виде не наблюдается. При горизонтальной поляризации кривые имеют монотонный характер, и для одних и тех же углов падения и длин волн коэффициент отражения выше, чем при вертикальной поляризации. С увеличением длины волны и электропроводности почвы модуль коэффициента отражения возрастает. Фаза коэффициента отражения при вертикальной поляризации резко изменяется и остается меньше или равной 180°. При горизонтальной поляризации фаза отраженной волны несколько больше или равна 180°.

Если поверхность идеально проводящая, то при любых углах падения волны происходит полное отражение и |R_в| = |R_г| = 1. Фаза отраженной волны при вертикальной поляризации Ф_в = 0, а при горизонтальной Ф_г = 180°, как следует из формул (1.69) и (1.73).

Для практического определения модуля и фазы коэффициента отражения служат специальные графики, представляющие собой зависимость R от угла падения волны на поверхность Земли [2].

Мгновенное значение напряженности электрического поля отраженной волны непосредственно над поверхностью Земли

а на некотором расстоянии h над поверхностью Земли

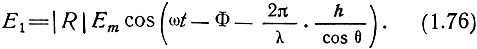
Для определения напряженности электрического поля отраженной волны при произвольной линейной поляризации падающей волны необходимо прежде всего разложить вектор Е‾ на вертикальную и горизонтальную составляющие:

где ξ - угол поляризации, т. е. угол между вектором E‾ и плоскостью падения волны.

Затем, используя известные коэффициенты отражения для каждой из этих составляющих, найдем составляющие напряженности электрического поля отраженной волны:

Выражения (1.77) представляют собой уравнения эллипса. Следовательно, в общем случае отраженная волна поляризована эллиптически, т. е. конец вектора Е‾ за один период описывает эллипс, лежащий в плоскости, перпендикулярной к плоскости падения волны (рис. 1.16).

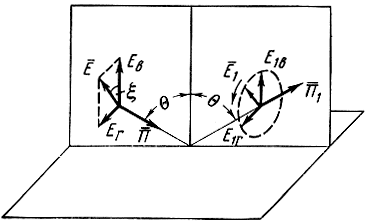
Рис. 1.16. Отражение волны в случае произвольной поляризации

Когда поверхность является идеальным проводником или идеальным диэлектриком, разность фаз Ф_в - Ф_г равна нулю или 180° и волна остается линейно-поляризованной. При этом коэффициент отражения

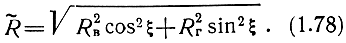
Плоскость поляризации при отражении изменяется, и угол поляризации становится равным

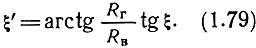
Линейная поляризация отраженной волны получается также при угле падения, равном углу полного преломления. В этом случае в отраженной волне вертикальная составляющая напряженности поля отсутствует, и волна поляризована всегда горизонтально.