§ 1.5. Виды поляризации радиоволн

Поляризацией радиоволны называют расположение вектора Е‾ в пространстве. Различают следующие виды поляризации плоской волны.

Линейная поляризация - вектор Е‾ меняясь во времени по величине, не меняет своего положения в пространстве. Выбрав декартовы координата так, чтобы ось х совпадала с направлением вектора Е‾ (рис. 1.7, а), можно записать для линейной поляризации

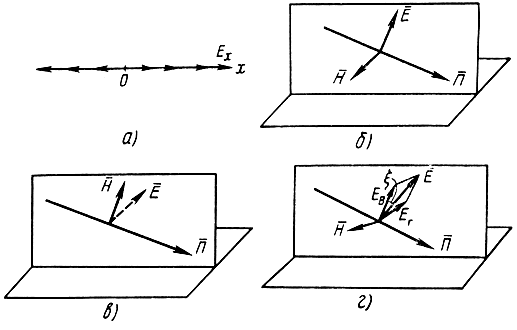
Рис. 1.7. Ориентация векторов напряженностей полей линейно-поляризованной волны: а - в свободном пространстве; б - на границе раздела двух сред (вертикальная поляризация); в - параллельно границе раздела (горизонтальная поляризация); г - произвольно (произвольная поляризация)

Если распространение линейно-поляризованной волны происходит вблизи границы раздела двух сред, то различают поляризацию вертикальную, когда вектор Е‾ лежит в плоскости падения волны (рис. 1.7, б), и горизонтальную, когда вектор Е‾ параллелен границе раздела (рис. 1.7, в).

Волну, поляризованную произвольно относительно границы раздела, можно разложить на две составляющие, одна из которых будет иметь вертикальную, а вторая горизонтальную поляризацию (рис. 1.7, г), причем обе составляющие вектора Е‾ меняются синфазно:

где ξ - угол между вектором Е‾ и плоскостью падения волны.

Круговая поляризация - вектор Е‾, оставаясь постоянным по величине, меняет направление во времени таким образом, что конец его описывает окружность.

В этом случае вектор Е‾ можно разложить на две составляющие (рис. 1.8):

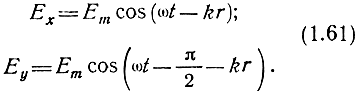
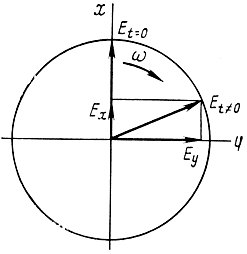
Рис. 1.8. Круговая поляризация радиоволны

Таким образом, волну с круговой поляризацией можно представить как суперпозицию двух волн с линейной поляризацией, причем векторы Е‾ этих волн ортогональны и сдвинуты по фазе на угол π/2, а амплитуды их равны.

С другой стороны, суперпозиция двух волн с круговой поляризацией, если амплитуды этих волн равны, а направления вращения векторов Е‾ противоположны, дает волну с линейной поляризацией. Действительно, можно записать:

для первой волны

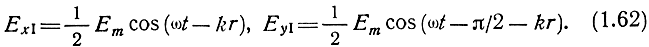
для второй волны

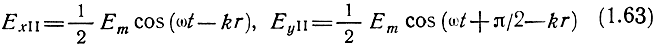
Просуммировав по координатам, получим

т. е. волну с линейной поляризацией.

Эллиптическая поляризация - вектор Е‾ меняется во времени по величине и направлению таким образом, что конец его описывает эллипс (рис. 1.9).

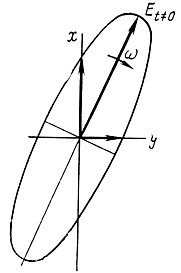
Рис. 1.9. Эллиптическая поляризация радиоволны

Вектор Е‾ волны с эллиптической поляризацией можно разложить на две составляющие:

где φ ≠ 0 или Е_xm ≠ Е_ym (могут выполняться одновременно оба условия).

В процессе распространения в среде поляризация радиоволны может меняться, например, благодаря более интенсивному поглощению одной из составляющих или различному изменению фаз составляющих.