
§ 1.4. Распространение плоских радиоволн в полупроводящей среде
Электромагнитные свойства полупроводящей среды характеризуются абсолютной диэлектрической проницаемостью εа (или относительной диэлектрической проницаемостью ε) и удельной электрической проводимостью γ. Будем рассматривать немагнитные среды, для которых μа = μ0.
Наиболее простым случаем является распространение радиоволн в идеальном диэлектрике, для которого γ = 0, ε = const. Распространение плоской волны в такой среде описывается уравнением [1]:
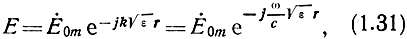
где Е - мгновенное значение напряженности электрического поля; Е0m - комплексная амплитуда напряженности электрического поля; r - расстояние, которое волна прошла в данной среде.
Комплексные амплитуды напряженностей магнитного Нm и электрического Еm полей связаны соотношением [1]
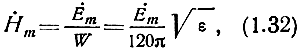
где 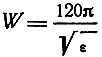
волновое сопротивление среды.
Электрическое и магнитное поля изменяются во времени синфазно.
Рассмотрим теперь, как изменится уравнение плоской волны в среде с потерями, т. е. в полупроводящей среде. Для сравнения запишем первое уравнение Максвелла соответственно для идеального диэлектрика и для диэлектрика с потерями:
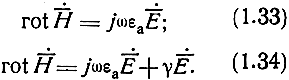
Если ввести понятие комплексной диэлектрической проницаемости
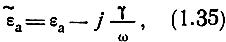
то уравнение (1.34) запишется формально точно так же, как и уравнение (1.33):
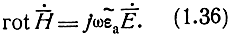
Использование комплексной диэлектрической проницаемости позволяет получить выводы, относящиеся к распространению радиоволн в полупроводящей среде, из соответствующих формул для идеального диэлектрика путем замены в них вещественной диэлектрической проницаемости εа на комплексное значение ε∼а (или заменой ε на ε∼). Величину ε∼а можно записать иначе, выразив в уравнении (1.35) круговую частоту через длину волны и подставив числовое значение электрической постоянной:
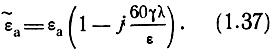
Величина 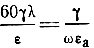
имеет физический смысл отношения плотности токов проводимости к плотности токов смещения. Действительно, поскольку ток проводимости равен γЕ, а ток смещения равен ωεaЕ, то, поделив одно на другое, получим
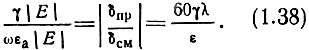
Следовательно, при 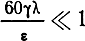
в среде преобладает плотность тока смещения, и среда по своим свойствам приближается к диэлектрику. Если же 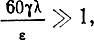
то в среде преобладает плотность тока проводимости, и среда по своим свойствам приближается к проводнику.
Мгновенное значение напряженности электрического поля при распространении плоской волны в полупроводящей среде записывается следующим образом:
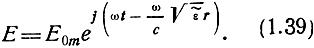
Обозначая
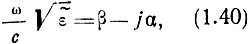
перепишем выражение (1.39) с учетом условия (1.40):
Е = Е0m еj (ωt - βr) - αr. (1.41)
Подставляя в уравнение (1.32) условие (1.40) и определяя модуль и фазу полученного выражения, запишем
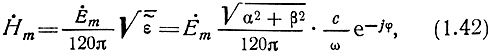
где
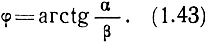
Из (1.43) видно, что составляющие электрического и магнитного поля сдвинуты по фазе на угол φ.
Величина α характеризует потери мощности в среде и называется коэффициентом поглощения. Физически потери обусловлены переходом энергии электромагнитных волн в тепловую энергию движения молекул.
Величина β характеризует изменение фазы волны, т. е. скорость распространения волны в данной среде.
Фазовую скорость распространения волны υф = dr / dt определяют, как скорость перемещения точки постоянной фазы, для которой
ωt - βr = const. (1.44)
Записав полный дифференциал этого выражения:
ωdt - βdr = 0,
можно определить υф:
υф = ω / β. (1.45)
При относительном перемещении передатчика и приемника с радиальной скоростью uR (составляющая скорости источника в направлении распространения волны) фаза воли (ωt - βr) меняется, что можно рассматривать, как изменение частоты колебаний. Принимаемая частота ωд, называемая частотой Допплера, оказывается равной
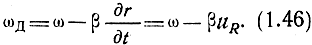
Разницу в величинах частот, передаваемых и принимаемых колебаний, называют допплеровским смещением частоты и определяют как
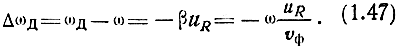
Частота принимаемых колебаний зависит от свойств среды, возрастает при удалении передатчика и приемника и снижается при их сближении.
Отношение
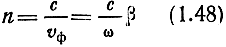
называют коэффициентом преломления среды.
Длина волны в среде с учетом (1.45) равна
λср = υф / f = 2π / β = λ / n. (1.49)
Выразим коэффициенты α и β через параметры среды. Согласно условию (1.40), можно записать
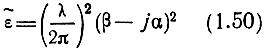
С другой стороны, из (1.37) следует, что
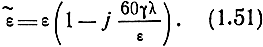
Правые части уравнений (1.50) и (1.51) равны. Приравнивая их действительные и мнимые части, а также решая совместно полученные уравнения, находим:
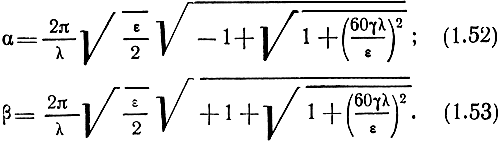
Перед внешними и внутренними радикалами берем положительные знаки, так как величины α и β считаем действительными, и за направление распространения принимаем направление возрастания расстояния r.
В некоторых встречающихся на практике случаях формулы могут быть значительно упрощены.
При ε >> 60γλ, пренебрегая в (1.53) вторым слагаемым, получаем:
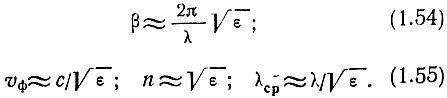
В формуле (1.52) нельзя просто пренебречь вторым слагаемым. Применяя к внутреннему радикалу бином Ньютона, получаем
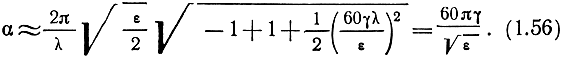
При ε << 60 γλ в выражениях (1.52) и (1.53) можно пренебречь единицей по сравнению с 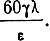
Тогда
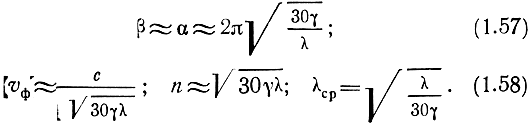

© RATELI.RU, 2010-2020
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
