§ 1.3. Область пространства, существенная при распространении радиоволн

При распространении радиоволн в свободном пространстве различные области пространства неодинаково влияют на формирование поля на некотором расстоянии от излучателя. Областью пространства, существенной при распространении радиоволн, называют область, в которой распространяется основная часть передаваемой мощности. Очевидно, что эта область охватывает пространство вблизи прямой, соединяющей точки расположения излучателя и приемной антенны. Размеры и конфигурацию области, существенной при распространении радиоволн, определяют исходя из принципа Гюйгенса - Френеля.

Согласно принципу Гюйгенса, каждая точка фронта распространяющейся волны является источником новой вторичной сферической волны. Полное поле определяется путем суммирования элементарных полей, созданных вторичными источниками, находящимися на некоторой поверхности, окружающей первичный источник. Построение, предложенное Френелем, позволяет наглядно истолковать этот принцип. Пусть в точке А (рис. 1.3, а) помещен источник, а в точке В - приемная антенна, причем расстояние АВ много больше длины волны:

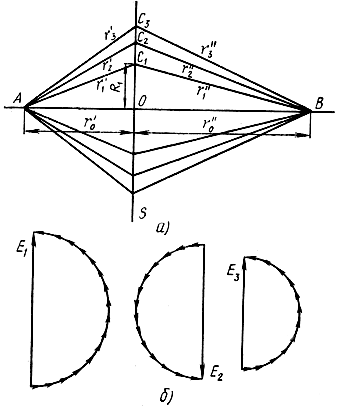
Рис. 1.3. Пояснение понятия зон Френеля: а - построение зон Френеля на плоскости; б - суммирование векторов напряженностей поля в пределах первой, второй и третьей зон Френеля

Пусть на некотором расстоянии от источника помещена бесконечная плоскость S, перпендикулярная к линии АВ. Эту плоскость выберем в качестве поверхности, на которой рассматриваются вторичные элементарные источники. Разобьем плоскость S на зоны Френеля, границы которых представляют собой концентрические окружности и определяются из условия, что путь, проходимый волной от точки А до границы зоны Френеля номера n и до точки В, больше пути от точки А до границы зоны Френеля номера (n + 1) и до точки В на половину длины волны. В обозначениях рис. 1.3, а это условие запишется в следующем виде:

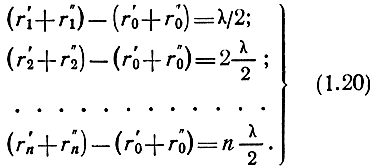
Элементарные вторичные источники, расположенные на внутренней и внешней границах каждой зоны, излучают волны, приходящие в точку В в противофазе. Проведем суммирование векторов напряженностей электрического поля, создаваемых элементами плоскости S, находящимися в пределах каждой зоны.

При выполнении условия (1.19) амплитуды векторов напряженностей электрического поля, создаваемых элементарными кольцевыми областями, мало отличаются друг от друга. Фазы их различны.

На рис. 1.3, б показано геометрическое суммирование векторов напряженностей поля вторичных источников при разбиении плоскости на кольца конечной ширины. Когда ширина колец, на которые разбивается плоскость, стремится к бесконечно малой величине, фазы вторичных источников меняются плавно и ломаная линия обращается в плавную кривую.

Векторы результирующих напряженностей поля, создаваемых соседними зонами Френеля, направлены в противоположные стороны, т. е. фазы их отличаются на 180°, а амплитуды уменьшаются с увеличением номера зоны:

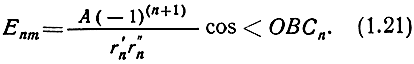
Здесь А - постоянная для данного источника излучения.

Результирующая напряженность поля, создаваемого всеми зонами Френеля, представляется в виде знакопеременного сходящегося ряда:

В силу условия (1.19) соседние члены ряда мало отличаются друг от друга и каждый из членов можно считать равным среднему арифметическому из двух соседних членов. Тогда, представив ряд (1.22) в виде

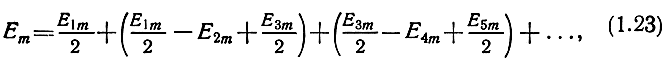
где lim_n→∞ Е_nm → 0 и величины в каждой из скобок близки к нулю, получаем, что результирующая напряженность поля равна половине значения, создаваемого первой зоной Френеля:

Поля, создаваемые зонами Френеля высших номеров, взаимно компенсируются.

Определим размеры зон Френеля. Обозначим радиус первой зоны Френеля R₁. Из ΔАС₁O и ΔВС₁O (см. рис. 1.3, а) определяем:

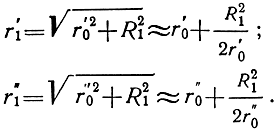
Суммируя правые и левые части этих равенств, получаем

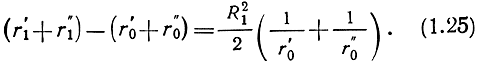
Из (1.25) и (1.20) находим радиус первой зоны Френеля:

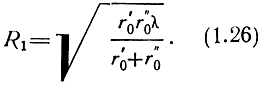
Внешние радиусы зон Френеля любого номера n находят из аналогичного построения:

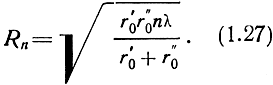
Площади всех зон Френеля одинаковы и равны

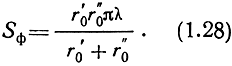
В плоскости распространения волны граница каждой из зон Френеля описывает эллипс. Действительно, если плоскость S перемещать вдоль линии АВ, то для любого положения этой плоскости будет справедливо равенство, описывающее границу данной зоны Френеля (рис. 1.4):

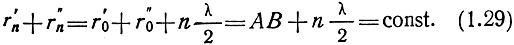
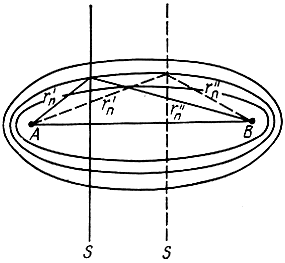
Рис. 1.4. Пространственные зоны Френеля

Равенство (1.29) является уравнением эллипса с полюсами в точках А и В. Следовательно, в пространстве первая зона Френеля представляет собой эллипсоид вращения, а зоны Френеля высших номеров - пространства между двумя эллипсоидами вращения. Наибольший размер поперечного сечения эллипсоиды имеют при r₀' = r₀". Радиус эллипсоида в этом сечении равен

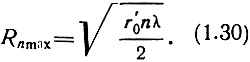
Таким образом, основной вклад в результирующее поле дают вторичные источники, расположенные на площади nS_ф, где n = 6÷8, и существенной при распространении радиоволн является область пространства, ограниченная зонами Френеля нескольких начальных номеров. Часто для упрощения считают, что существенной при распространении радиоволн является область, ограниченная эллипсоидом с поперечным сечением, равным первой зоне Френеля.

С укорочением длины волны эллипсоиды уменьшаются в сечении и в пределе при λ → 0 превращаются в прямую, называемую лучом. Поэтому на очень коротких, например световых, волнах, можно считать, что распространение происходит по прямому лучу. Введение понятия луча значительно упрощает решение задач распространения волн и им пользуются в ряде случаев также в диапазоне радиоволн.

Рассмотрение распространения радиоволн в свободном пространстве или в однородной среде как с позиции волновой теории (принцип Гюйгенса, построение зон Френеля), так и с использованием понятия луча дает одинаковый результат. При наличии в среде неоднородностей, препятствий получаемый результат можно объяснить с помощью зон Френеля.

Рассмотрим два вида неоднородностей, препятствий на пути распространения электромагнитной волны: непрозрачный экран с круглым отверстием и непрозрачную полуплоскость.

Пусть на пути распространения волны расположен непрозрачный экран с круглым отверстием, центр которого совпадает с линией АВ (рис. 1.5, а).

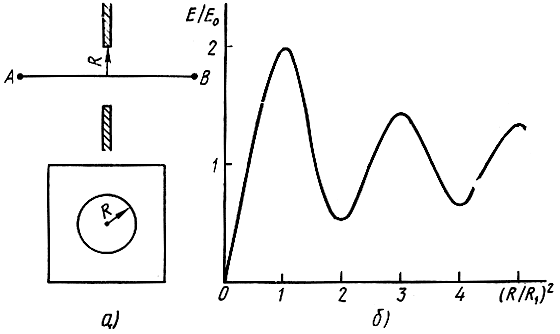
Рис. 1.5. Дифракция радиоволн на круглом отверстии в непрозрачном экране: а - схема расположения экрана; б - зависимость величины напряженности поля за экраном от отношения площадей отверстия и первой зоны Френеля

Если радиус отверстия плавно увеличивать от R = 0, то напряженность поля за экраном в точке В будет возрастать (рис. 1.5, б) и достигнет максимума при R = R₁. Дальнейшее изменение величины напряженности поля носит осциллирующий характер; напряженность поля максимальна при радиусе отверстия, равном радиусу зоны Френеля нечетного номера, и минимальна при радиусе отверстия, равном радиусу зоны Френеля четного номера. С увеличением номера зоны Френеля амплитуда осцилляции уменьшается и напряженность поля стремится к величине поля в свободном пространстве Е₀.

Перемещая экран вдоль линии АВ и одновременно меняя радиус отверстия в экране таким образом, чтобы поле за экраном оставалось постоянным, можно получить конфигурацию пространственных зон Френеля.

Пусть на пути распространения АВ помещена непрозрачная полуплоскость так, что се край лежит ниже линии АВ (рис. 1.6, а). Расстояние d назовем просветом, причем в этом случае величину d считают отрицательной. Если край полуплоскости лежит выше линии АВ (рис. 1.6, б), то значение d считают положительным. Когда d положительно и достаточно велико, много больше радиуса первой зоны Френеля, поле за экраном практически отсутствует. При уменьшении расстояния напряженность поля возрастает, как видно из графика рис. 1.6, в. Однако при d = 0 она равна половине напряженности поля в свободном пространстве, так как половина площади, существенной при распространении радиоволн, перекрыта препятствием. При изменении величины d в сторону отрицательных значений изменение напряженности поля носит осциллирующий характер, что связано с попеременным перекрытием четных и нечетных зон Френеля. Глубина осцилляции здесь не так велика, как в случае круглого отверстия, так как основная площадь зон Френеля уже открыта.

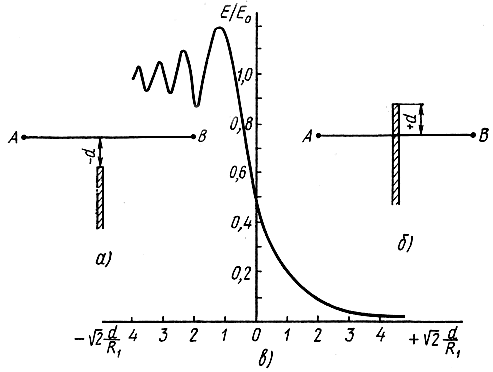
Рис. 1.6. Дифракция радиоволн на краю экрана: а - открытая трасса; б - закрытая трасса; в - зависимость величины напряженности поля от нормированной высоты просвета  

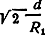
Из приведенных примеров ясно, что при наличии неоднородностей, препятствий трактовка с использованием понятия луча не может дать правильного объяснения происходящих явлений.