
§ 2.3. Поле элементарного электрического вибратора, поднятого над плоской земной поверхностью
Влияние земной поверхности на распространение радиоволн наиболее просто учесть тогда, когда передающая и приемная антенны подняты над однородной земной поверхностью на высоту в несколько длин волн. Практически поднять антенну на такую высоту можно только в диапазоне УКВ. Если волна достигает земной поверхности на значительном (в масштабе длины волны) расстоянии от излучателя, то участок фронта волны вблизи земной поверхности можно считать плоским. При небольшой протяженности линии связи Землю также можно считать плоской.
На границе раздела воздух - Земля происходит отражение волны, причем напряженность электрического поля отраженной волны определяется при помощи коэффициентов отражения (1.69), (1.73), поле в месте приема является результатом интерференции полей прямой волны и волны, отраженной от земной поверхности (рис. 2.7).
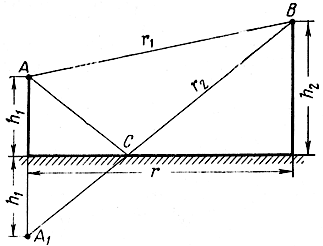
Рис. 2.7. Схема распространения радиоволн в случае, когда передающая и приемная антенны подняты над поверхностью Земли
Здесь прямая волна распространяется по пути АВ, а отраженная - по пути АСВ. Обозначим через r длину линии связи, а через h1 и h2 высоты расположения передающей и приемной антенн. Предположим, что выполняется условие h >> λ и h2 >> λ.
Путь отраженной волны АСВ можно заменить равным ему путем А1СВ, если считать, что источником отраженной волны является вибратор, находящийся на расстоянии h1 под поверхностью, и влияние Земли заменить действием второго вибратора.
Мгновенное значение напряженности электрического поля вибратора, находящегося в точке A, т. е. напряженности поля прямой волны,
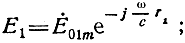
мгновенное значение напряженности электрического поля вибратора, находящегося в точке А1, т. е. напряженности поля отраженной волны,
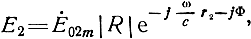
где E⋅01m и E⋅02m - комплексные амплитуды напряженностей электрического поля вибраторов в свободном пространстве, которые в соответствии с уравнением (1.11) изменяются обратно пропорционально расстояниям r1 и r2; |R| е-jФ - коэффициент отражения от поверхности Земли.
Наибольший практический интерес представляют условия
r >> h1 и r >> h2.
В этом случае прямые, проведенные из точек А, А1 в точку приема В, можно считать параллельными. Из рис. 2.8 легко выразить разность расстояний r1 и r2 через высоту h1 и угол падения волны на поверхность:
r2 - r1 = 2 h1 cos θ. (2.4)
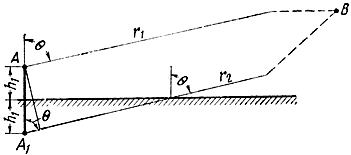
Рис. 2.8. Определение разности расстояний, пройденных прямой и отраженной волнами
Разность расстояний r1 и r2, пройденных прямой и отраженной волнами, невелика и при вычислении амплитуд напряженностей электрического поля E01m и Е02m ею можно пренебречь, считая
E01m ≈ Е02m ≈ E0m. (2.5)
При нахождении фазы поля такое допущение делать нельзя. Учитывая выражения (2.4) и (2.5), можно записать
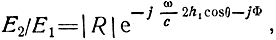
откуда
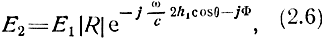
Мгновенное значение результирующей напряженности электрического поля
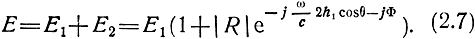
Амплитуда результирующей напряженности поля равна модулю последнего выражения:
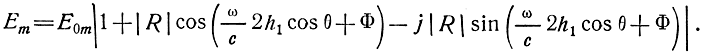
Вычисляя модуль, имеем
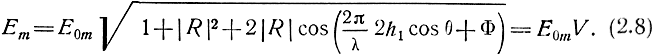
В правую часть (2.8) входит два сомножителя: Е0m - поле в свободном пространстве и V - множитель влияния Земли, показывающий характер искажений, вносимых присутствием Земли в поле излучателя.
Полученная формула носит название интерференционной. Рассмотрим некоторые частные случаи ее применения.
Вертикальный вибратор
В случае, когда излучателем является элементарный вертикальный вибратор, следует учитывать диаграмму направленности самого вибратора F(ξ) = cos ξ = sin θ. Амплитуда напряженности электрического поля Е01m определяется формулой (1.8):
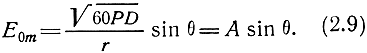
В результате подстановки (2.9) выражение (2.8) примет следующий вид:
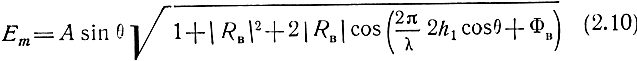
Вертикальный вибратор создает главным образом вертикально-поляризованную волну, поэтому следует пользоваться значениями модуля и фазы коэффициента отражения для вертикальной поляризации.
Проанализируем, как зависят направленные свойства вибратора от параметров поверхности, над которой он расположен.
Прежде всего рассмотрим случай идеально проводящей поверхности (γ = ∞). Для всех углов падения волны на поверхность |Rв| = 1, Фв = 0. Из уравнения (2.10) имеем
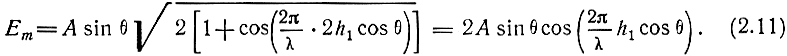
Входящий в эту формулу множитель 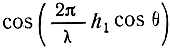
указывает на существование интерференционных максимумов и минимумов при достаточно большом отношении h1/λ.
Действительно, при
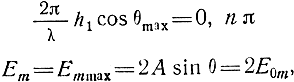
а при
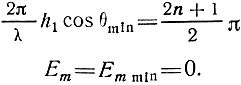
Таким образом, максимальное излучение наблюдается в направлениях, для которых
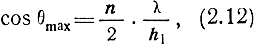
а минимальное - в направлениях, для которых
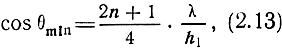
где n - целое число или нуль.
Первый минимум излучения (нуль) имеет место при 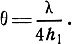
Следовательно, чем выше расположен вибратор над поверхностью Земли, тем уже первый лепесток его диаграммы направленности.
Вдоль поверхности, в горизонтальном направлении имеется максимум излучения, так как при θ = 90°
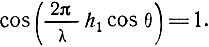
В вертикальном направлении вибратор не излучает. С уменьшением угла θ амплитуды лепестков Em max уменьшаются за счет влияния диаграммы направленности самого вибратора.
Таким образом, практически независимо от направленных свойств излучателя диаграмма направленности в вертикальной плоскости приобретает многолепестковый характер. Так, например, при λ = 10 см и h1 = 1 м число максимумов достигает 21.
Диаграмма направленности вертикального вибратора, расположенного над идеально проводящей поверхностью при h1/λ = 2,5, изображена на рис. 2.9.
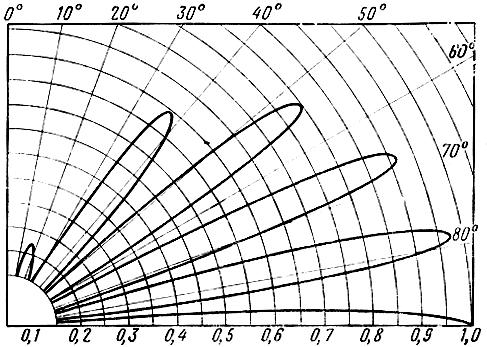
Рис. 2.9. Диаграмма направленности вертикального вибратора, расположенного на высоте h1 = 2,5λ над идеально проводящей поверхностью
Следует отметить, что при расположении вибратора над идеально проводящей поверхностью полученные формулы справедливы для любых высот h1 и h2.
Предположим теперь, что поверхность Земли по своим свойствам близка к идеальному диэлектрику, т. е. 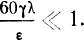
Этот случай наиболее важен, так как соответствует распространению волн УКВ диапазона над сушей и волн сантиметрового диапазона над сушей и морем.
Анализ диаграммы направленности усложняется тем, что с изменением угла θ резко изменяется коэффициент отражения (см. рис. 1.15).
Для больших расстояний и небольших высот приемной антенны можно считать θ >> θ0. Тогда Фв = 180°, и выражение (2.10) примет вид
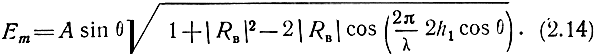
Поле в вертикальной плоскости вибратора имеет лепестковую структуру, причем максимумы излучения появляются в направлениях, приближенно определяемых условием 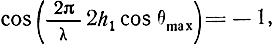
откуда
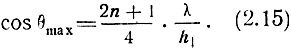
Для более точного определения положения максимумов излучения следует учитывать зависимость |RB| от θ. Величина Еm mах определяется по формуле
Em max = A(1 + |Rв|)sin θ = E0m (1 + |Rв|). (2.16)
Первый максимум излучения наблюдается при 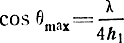
и чем выше расположен вибратор над поверхностью Земли, тем больше первый лепесток его диаграммы направленности "прижат" к Земле.
Минимумы излучения наблюдаются в направлениях, для которых
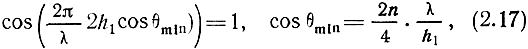
причем
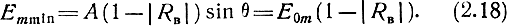
Таким образом, направления максимумов и минимумов излучения меняются местами по сравнению со случаем идеально проводящей поверхности, а напряженность поля в минимумах не равна нулю, поскольку |Rв| < 0. Вдоль земной поверхности излучение отсутствует, так как для скользящих лучей |Rв| = 1.
При значительной высоте расположения приемной антенны может оказаться, что θ < θ0. Тогда Фв = 0 и выражение (2.10) перепишется в виде
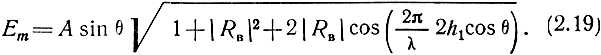
Максимумы излучения появляются в направлениях, для которых
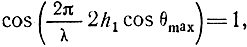
а минимумы - в направлениях, для которых
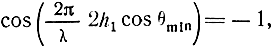
т. е. положение лепестков такое же, как в случае идеально проводящей поверхности.
Амплитуда напряженности поля в максимумах и минимумах интерференционных лепестков по-прежнему определяется выражениями (2.16) и (2.18).
Диаграмма направленности вертикального вибратора, расположенного над идеальной диэлектрической поверхностью при h1 = 3, изображена на рис. 2.10.
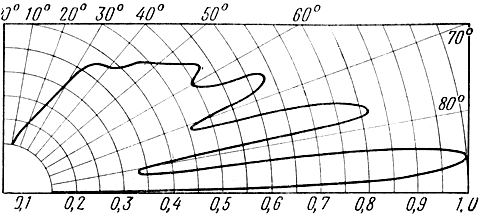
Рис. 2.10. Диаграмма направленности вертикального вибратора, расположенного на высоте h1 = 3 λ над поверхностью, представляющей собой идеальный диэлектрик (ε = 1,5)
В случае полупроводящей поверхности фаза коэффициента отражения принимает различные значения и |Rв| меняется в широких пределах. Однако лепестковая структура поля сохраняется и может быть построена для любого сочетания γ и ε. Вдоль поверхности Земли, как и ранее, излучение отсутствует, поскольку |Rв| = 1 и Фв = 180°.
Горизонтальный вибратор
Рассмотрим электрическое поле горизонтального вибратора в его экваториальной плоскости.
В экваториальной плоскости вибратор не обладает направленными свойствами F(χ) = 1 и создает горизонтально-поляризованную волну. Следовательно, выражение (2.8) можно записать в виде
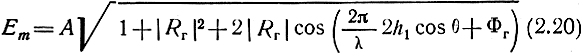
В случае идеально проводящей поверхности (γ = ∞) для всех углов падения волны на поверхность |Rг| = 1, Фг = 180° и амплитуда напряженности поля
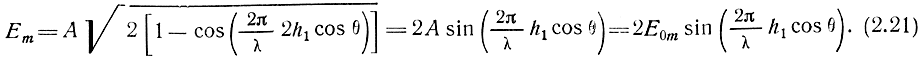
Структура поля лепестковая, как и для вертикального вибратора, но направления максимумов и минимумов излучения меняются местами по отношению к полю вертикального вибратора над идеально проводящей поверхностью:
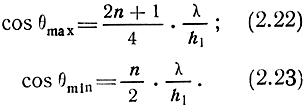
Вдоль земной поверхности излучение отсутствует. Амплитуды лепестков не меняются в зависимости от угла θ. Возможно излучение вверх (θ = 0) при условии
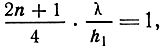
т. е. когда h равно нечетному числу λ/4. Диаграмма направленности горизонтального вибратора, расположенного над идеально проводящей поверхностью при h1 = 2,5 λ, изображена на рис. 2.11.
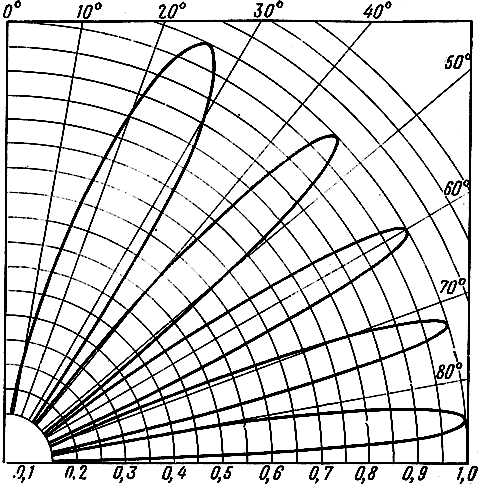
Рис. 2.11. Диаграмма направленности горизонтального вибратора, расположенного на высоте h1 = 2,5 λ, над идеально проводящей поверхностью
Если поверхность Земли является идеальным диэлектриком, то для горизонтально-поляризованной волны при всех углах падения волны на поверхность Фг = 180°. Следовательно, амплитуда напряженности электрического поля
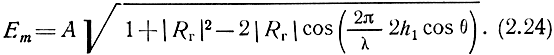
Полученное выражение отличается от уравнения (2.14) только заменой величин Rв на Rг и отсутствием множителя sin θ. Поэтому направление максимумов и минимумов излучения определяется здесь теми же соотношениями (2.15) и (2.17).
Вдоль земной поверхности излучение отсутствует. Для других направлений
Еm max = A (1 + |Rг|) = Е0m (1 + |Rг|); (2.25)
Еm min = A (1 - |Rг|) = Е0m (1 - |Rг|). (2.26)
Диаграмма направленности для этого случая изображена на рис. 2.12.
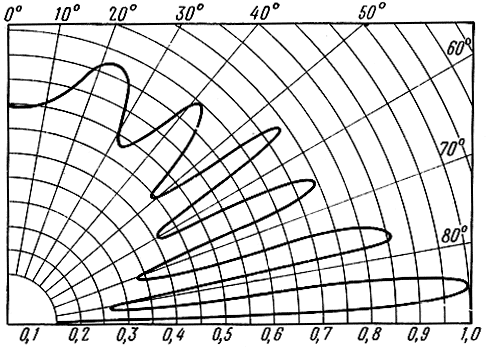
Рис. 2.12. Диаграмма направленности горизонтального вибратора, расположенного на высоте h1 = 3 λ над поверхностью, представляющей собой идеальный диэлектрик (ε = 1,5)
С уменьшением угла θ уровень лепестков уменьшается не так значительно, как при вертикальной поляризации. При этом диаграмма направленности вибратора в его горизонтальной плоскости соответствует диаграмме направленности вибратора в плоскости вектора Е‾.
Было рассмотрено поле горизонтального вибратора в его экваториальной плоскости. В других направлениях горизонтальный вибратор излучает и горизонтально- и вертикально-поляризованные составляющие напряженности электрического поля. Напряженность поля каждой из составляющих определяют отдельно и затем находят результирующую напряженность поля. При этом поле оказывается эллиптически поляризованным с преобладающей горизонтальной составляющей.
Распределение поля в вертикальной плоскости вибратора при наличии полупроводящей поверхности мало отличается от распределения поля в случае идеальной диэлектрической поверхности.

© RATELI.RU, 2010-2020
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
