§ 2.8. Поле вертикального электрического вибратора, расположенного вблизи земной поверхности

Передающие антенны средних и длинных волн выполняют чаще всего в виде мачт или башен, расположенных в непосредственной близости от поверхности Земли. По принципу действия они эквивалентны вертикальным заземленным вибраторам. В некоторых случаях антенны коротких волн и УКВ также располагают вблизи поверхности Земли, например, автомобильные антенны или антенны переносных радиостанций.

Структура поля волны вблизи земной поверхности

Рассмотрим наиболее простой случай, когда излучатель расположен вблизи идеально проводящей поверхности. К этому случаю близко распространение длинных волн над морем. На рис. 2.26 изображена структура поля вертикального вибратора вблизи идеально проводящей поверхности.

Рис. 2.26. Структура поля вертикального вибратора, расположенного вблизи идеально проводящей поверхности

Энергия, излученная таким вибратором, распространяется только в верхнем полупространстве над плоскостью и, следовательно, плотность ее в два раза больше, чем плотность энергии в свободном пространстве. Напряженность поля увеличивается в √2 по сравнению с напряженностью поля в свободном пространстве. Диаграмма направленности подобной антенны имеет максимум излучения вдоль земной поверхности. Амплитуда напряженности электрического поля вблизи поверхности

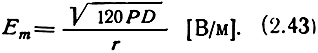
Согласно граничным условиям вектор напряженности электрического поля Е^- направлен нормально к поверхности, а следовательно, вектор Пойнтинга направлен параллельно поверхности.

Когда источником радиоволн является горизонтальный вибратор, создающий в направлении, перпендикулярном к оси вибратора только горизонтальную составляющую вектора Е^-, в силу граничных условий напряженность электрического поля вблизи идеально проводящей поверхности равна нулю.

Если поверхность не является идеальным проводником, то напряженность поля отлична от нуля, но поле горизонтального вибратора значительно слабее поля вертикального вибратора, поэтому наибольший интерес представляет изучение структуры поля, создаваемого вертикальным вибратором.

На рис. 2.27 изображена структура поля вертикального вибратора, расположенного вблизи полупроводящей земной поверхности.

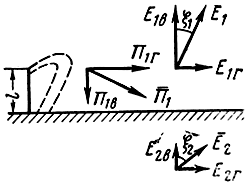
Рис. 2.27. Структура поля вертикального вибратора, расположенного вблизи полупроводящей земной поверхности

Если поверхность, вблизи которой расположен излучатель, не является идеальным проводником, то часть энергии радиоволн, распространяющихся от антенны, проникает в глубь земной поверхности. Следовательно, помимо составляющей вектора Пойнтинга П_г, направленной вдоль поверхности, имеется составляющая П_в, направленная перпендикулярно к поверхности Земли.

Суммарный вектор Пойнтинга П^-₁ оказывается наклоненным к земной поверхности под некоторым углом, а следовательно, и вектор напряженности электрического поля Е^-₁ направлен к земной поверхности под углом, не равным 90°. Поэтому при распространении радиоволны над полупроводящей поверхностью, помимо вертикальной составляющей вектора напряженности электрического поля Е_1в, имеется горизонтальная составляющая Е_1г.

Выясним соотношение между вертикальными и горизонтальными составляющими поля в воздухе и в земле. Для этого воспользуемся приближенными граничными условиями Леонтовича [1]. Граничные условия Леонтовича для плоской однородной поверхности заключаются в том, что если вторая среда - поверхность Земли - обладает комплексной диэлектрической проницаемостью, намного превышающей диэлектрическую проницаемость первой среды - воздуха:

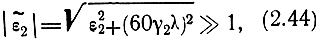
то волну, проникающую в глубь земной поверхности, приближенно можно считать плоской, распространяющейся нормально к поверхности Земли. Действительно, если волна падает на поверхность и соблюдается условие (2.44), то угол преломления определяется согласно формулам (1.66) и (1.37):

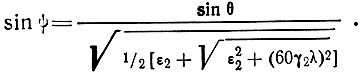
Отсюда следует, что при |ε₂| >> 1 угол ψ мал и волна распространяется во второй среде почти по нормали к поверхности.

Согласно выражению (1.49), волна во второй среде сильно укорачивается:

и на протяжении этой длины волны электромагнитное поле вдоль поверхности меняется мало, т. е. волну можно считать плоской.

Для плоской волны во второй среде справедливо соотношение между комплексными амплитудами напряженностей электрического и магнитного полей [см. формулу (1.42)]:

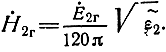
Согласно строгим граничным условиям тангенциальные составляющие электрического и магнитного полей на границе раздела равны

Из выражения для H^·_2г и формулы (2.45) вытекает, что соотношение между тангенциальными составляющими электрического и магнитного полей над полупроводящей поверхностью с большим значением |ε˜₂| определяется параметрами этой поверхности:

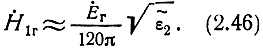
Формула (2.46) называется приближенным граничным условием Леонтовича.

Пусть вертикальный вибратор создает над полупроводящей поверхностью Земли вертикальную составляющую вектора напряженности электрического поля Е^·_1в. Приближенно волну в первой среде можно считать плоской. Следовательно, величины Е^·_1в и H^·_1г связаны соотношением

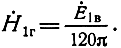
Учитывая формулу (2.46), получаем соотношение между вертикальной и горизонтальной составляющими вектора напряженности электрического поля вблизи земной поверхности:

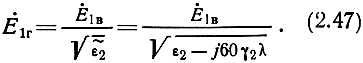
Строгие граничные условия (2.45) дают связь между Е^·_1г и Е^·_2г, откуда

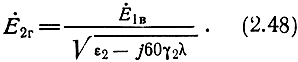
Используя граничные условия для нормальных составляющих вектора напряженности электрического поля:

Определим вертикальную составляющую во второй среде:

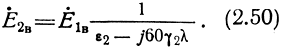
Таким образом, все составляющие напряженности электрического поля выражены через вертикальную составляющую.

Из выражений (2.47), (2.48), (2.49) видно, что при соблюдении условия (2.44) в первой среде вертикальная составляющая напряженности поля больше горизонтальной, а во второй среде горизонтальная составляющая больше вертикальной.

Горизонтальная и вертикальная составляющие напряженности поля имеют сдвиг по фазе.

Представляя знаменатель формулы (2.47) в виде модуля и фазового множителя, получим мгновенное значение напряженности поля над поверхностью Земли:

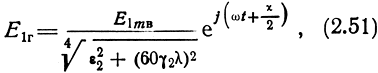
где

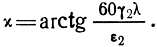
Из (2.50) следует, что сдвиг фаз между вертикальными составляющими поля Е_1в и Е_2в равен χ, а между вертикальной Е_2в и горизонтальной Е_2г составляющими (-χ/2). Сдвиги фаз между вертикальными и горизонтальными составляющими приводят к тому, что результирующее поле над поверхностью Земли и в глубине Земли поляризовано эллиптически в вертикальной плоскости. Наклоны больших осей эллипсов поляризации определяются углами ξ₁ и ξ₂ (см. рис. 2.27):

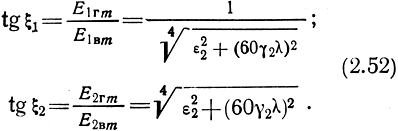
Таким образом, если излучателем является вертикальный вибратор и основная часть энергии передается вертикально-поляризованной волной, то поле вблизи поверхности Земли имеет и горизонтальные составляющие Е_1г, Е_2г. ЭТО позволяет применять в качестве приемных антенн горизонтальный провод, растянутый вблизи поверхности Земли над или под Землей в направлении распространения волны. Такая приемная антенна конструктивно более удобна, чем высокая мачта, необходимая для приема вертикально-поляризованной волны.

Расчет вертикальной составляющей напряженности электрического поля

Метод расчета разработан для определения вертикальной составляющей напряженности электрического поля вибратора, расположенного на поверхности Земли. Остальные составляющие связаны с ней соотношениями (2.47)÷(2.50).

Напряженность электрического поля при распространении волны над полупроводящей поверхностью меньше, чем при распространении волны над идеально проводящей поверхностью.

Энергия радиоволны, проникающей в полупроводящую поверхность Земли, частично теряется в ней.

Уменьшение напряженности электрического поля при распространении волны над полупроводящей поверхностью учитывается введением в уравнение (2.43) множителя ослабления |W|:

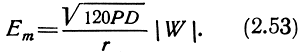
Определение зависимости множителя ослабления от параметров трассы и длины волны весьма сложно с математической точки зрения. Впервые решение этой задачи предложил в 1909 г. А. Зоммерфельд. Решение было дано в интегральной форме, не пригодной для инженерных расчетов. В 1923-1925 гг. советский ученый М. В. Шулейкин и голландский ученый Б. Ван-дер-Поль придали этому решению вид, удобный для расчетов. В результате этого был получен график, показывающий зависимость множителя ослабления |W| от параметра р. Параметр ρ зависит от длины волны, электрических свойств почвы, протяженности трассы и называется численным расстоянием:

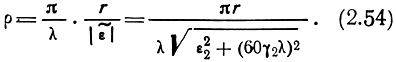
Зависимость |W| от р изображена на рис. 2.28, где величины |W| и ρ отложены в логарифмическом масштабе.

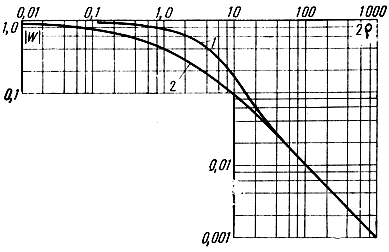
Рис. 2.28. Зависимость множителя ослабления |W| от численного расстояния р: 1 - 60 γλ > ε; 2 - 60 γλ < ε

Расчет напряженности поля и множителя ослабления можно проводить также по приближенной формуле

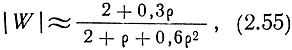
которая аппроксимирует кривую 1 на рис. 2.28.

Из графика и формулы видно, что при небольших значениях р множитель ослабления |W| слабо зависит от ρ, т. е. мало меняется с изменением расстояния, длины волны и электрических свойств почвы. При ρ > 20 величина |W| изменяется обратно пропорционально численному расстоянию ρ, причем

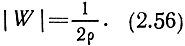
Следует обратить внимание на то, что напряженность поля при распространении радиоволн над полупроводящей поверхностью изменяется с расстоянием не по экспоненте, как при распространении волн в поглощающей среде, а по более сложному закону, изображенному графически на рис. 2.28.

Пользуясь этим графиком и формулой (2.53), легко проследить зависимость напряженности электрического поля от расстояния. При малых расстояниях численное расстояние р мало и множитель ослабления |W| ≈ 1, т. е. напряженность поля изменяется обратно пропорционально расстоянию. При больших расстояниях численное расстояние ρ велико и множитель ослабления |W| пропорционален 1/r) т. е. напряженность электрического поля изменяется обратно пропорционально квадрату расстояния. С увеличением длины волны, проводимости и диэлектрической проницаемости почвы величина ρ уменьшается, а следовательно, возрастают множитель ослабления и напряженность электрического поля.

В некоторых встречающихся на практике случаях выражение для ρ (2.54) может быть упрощено. Если среда приближается по своим свойствам к диэлектрику, то ε₂ >> 60γ₂λ. Пренебрегая в формуле (2.54) вторым слагаемым, получим

Если плотность токов проводимости в поверхности Земли значительно превышает плотность токов смещения, то 60γ₂λ >> ε₂ и можно пренебречь первым слагаемым в формуле (2.54). Тогда выражение для ρ запишется следующим образом:

т. е. поле убывает с укорочением длины волны по квадратичному закону. Этот случай встречается на практике более часто, так как соответствует диапазонам средних и длинных волн, для излучения которых применяются антенны, расположенные вблизи поверхности Земли.