§ 2.7. Распространение радиоволн над неровной или неоднородной трассой, когда антенны подняты высоко над поверхностью земли

Обычно на земной поверхности имеются более или менее выраженные неровности, наличие которых влияет на распространение радиоволн. В общем случае учесть это влияние не представляется возможным. Для расчета напряженности электрического поля в каждом конкретном случае необходимо построить профиль трассы и в зависимости от характера этого профиля вести расчет тем или иным методом.

Рассмотрим, как влияют на распространение радиоволн типичные виды неровностей земной поверхности: мелкие неровности (шероховатая поверхность); пологие холмы, город; одиночное препятствие (гора, высокий дом).

Отражение радиоволн от неровной земной поверхности

При падении волны на совершенно ровную плоскую поверхность направление отраженной волны подчиняется закону геометрической оптики (угол отражения равен углу падения). Такое отражение называется зеркальным. Только при нормальном падении волны на поверхность отраженная волна возвращается к излучателю.

Если поверхность Земли неровная, то радиоволны отражаются в различных направлениях, в том числе в обратном направлении (рис. 2.17).

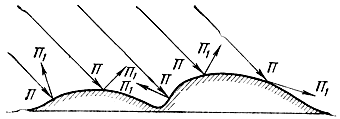
Рис. 2.17. Рассеяние радиоволн при отражении от неровной земной поверхности

Отражение от неровной поверхности является рассеянным, причем напряженность поля отраженной волны в зеркальном направлении меньше, чем в случае отражения от ровной поверхности. При рассмотрении отражения радиоволн от неровной поверхности говорят об эффективном коэффициенте отражения в зеркальном направлении.

Расчет эффективного коэффициента отражения от неровной поверхности весьма сложен. В диапазоне дециметровых и сантиметровых волн эффективный коэффициент отражения от неровной поверхности обычно определяют путем измерений зависимости этой величины от угла падения волны на поверхность и длины волны для различных видов земной поверхности (рис. 2.18).

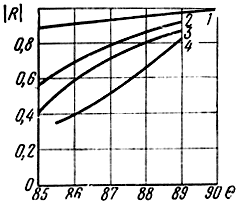
Рис. 2.18. Зависимости эффективного коэффициента отражения от угла падения волны на поверхность и длины волны: 1 - теоретическая зависимость для ровной поверхности; 2 - λ = 26 см; 3 - λ = 9 см; 4 - λ = 3 см - экспериментальные зависимости для неровной поверхности

Из графиков видно, что измеренная величина эффективного коэффициента отражения тем больше отличается от рассчитанной для идеально ровной поверхности, чем короче длина волны и чем больше угол падения волны на поверхность. Качественно такую зависимость можно пояснить следующим образом.

Пусть плоская волна отражается от поверхности с неровностями, наибольшая высота которых равна h (рис. 2.19). Часть мощности падающей волны отразится на нижнем уровне неровностей a - a₁, другая часть - на верхнем уровне b - b₁.

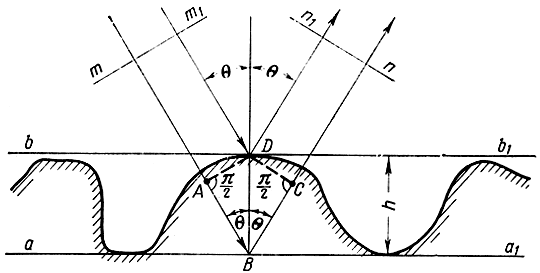
Рис. 2.19. Искажение фронта волны при отражении от неровной поверхности Земли

Плоскость m - m₁, перпендикулярная к направлению распространения падающей волны, является плоскостью равных фаз. Определим фазовые соотношения на плоскости n - n₁, перпендикулярной к направлению распространения отраженной волны. Очевидно, что наибольшая разность фаз окажется между волнами, отраженными от верхнего (точка D) и нижнего (точка В) уровней неровностей. Разность хода лучей mn и m₁n₁ составляет 2АВ = 2h cosθ, что приводит к сдвигу фаз между лучами, равному

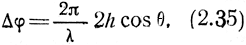
Считают, что если фазовые искажения на плоскости n - n₁ не превышают π/2, то волну можно считать плоской и влиянием неровностей на отражение волны пренебречь. Из этого условия можно получить допустимую высоту неровностей, т. е. высоту неровностей, при которых отражение можно считать зеркальным:

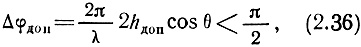
откуда

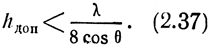
Соотношение (2.37) называется критерием Релея. Этот критерий показывает, что при данной высоте неровностей отражение ближе к зеркальному для полого падающих лучей. Влияние неровностей земной поверхности сказывается тем сильнее, чем короче длина волны. В диапазоне УКВ даже небольшие неровности (шероховатости) Земли вызывают рассеянное отражение волн.

Неровной поверхностью для УКВ является также поверхность взволнованного моря, причем степень неровности зависит от силы волнения.

В диапазоне средних и длинных волн неровностями являются холмы высотой в десятки ветров и крупные строения.

Поле излучателя, поднятого над неровной или неоднородной земной поверхностью

По законам геометрической оптики отражение радиоволн происходит в некоторой точке. В действительности же, согласно волновой теории, отраженная волна формируется участком земной поверхности, окружающим точку отражения.

Если передающая и приемная антенны разнесены на расстояние r, то, как было сказано выше, в точку приема приходят прямая и отраженная волны. Для каждой из этих волн имеется область, существенная при распространении. Для прямой волны эта область представляет собой эллипсоид вращения с полюсами в точках А и В. Для отраженной волны строят такой же эллипсоид с одним фокусом, находящимся в точке расположения фиктивного источника А₁. Область пересечения эллипсоида вращения с поверхностью Земли представляет собой область, существенную при отражении радиоволн, и имеет конфигурацию эллипса, большая ось которого вытянута в направлении распространения волны (рис. 2.20). Эту область называют первой зоной Френеля при отражении.

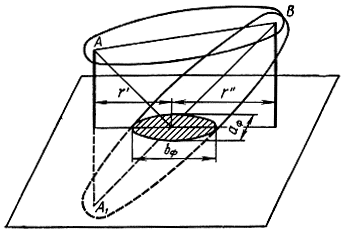
Рис. 2.20. Участок земной поверхности, формирующий отраженную волну

Размеры малой и большой полуосей эллипса соответственно равны:

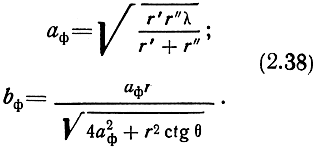
Здесь r′ и r″ - расстояния от концов трассы до точки геометрического отражения; r - протяженность трассы (r = r′ + r″); θ - угол падения волны.

При нормальном падении волны на поверхность область, существенная при отражении, представляет собой окружность радиуса, равного радиусу первой зоны Френеля (1.26).

Размеры области, существенной при отражении, на реальных УКВ трассах могут составлять многие километры в продольном и десятки метров в поперечном направлении.

При идеально ровной однородной поверхности результаты, получаемые по волновой теории, в точности совпадают с данными геометрической оптики. При неровной или неоднородной отражающей поверхности законы геометрической оптики становятся неприменимы.

Если распространение радиоволн происходит над неровной поверхностью, то рассеяние радиоволн неровностями, находящимися в области, существенной при отражении, приводит к уменьшению эффективного коэффициента отражения, а следовательно, к сглаживанию максимумов и минимумов интерференционной диаграммы направленности (рис. 2.21).

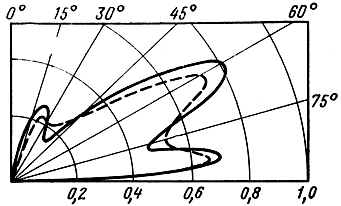
Рис. 2.21. Распределение напряженности поля над поверхностями с одними и теми же электрическими свойствами: ^___ ровная поверхность; --- неровная поверхность

В том случае, когда это нежелательно, приходится выравнивать участок земной поверхности, соответствующий эллипсу, формирующему отраженную волну.

Напряженность электрического поля над неровной поверхностью рассчитывают по формулам (2.10) или (2.20), но с учетом эффективного коэффициента отражения. Излучение в направлениях интерференционных максимумов и минимумов при слабо направленных излучателях описывается для вертикальной поляризации выражениями (2.16) и (2.18), а для горизонтальной поляризации - выражениями (2.25) и (2.26). Измерение отношения величины напряженности поля в максимуме и минимуме излучения позволяет определить эффективный коэффициент отражения для реальной земной поверхности. Действительно,

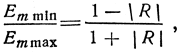
откуда

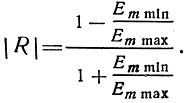
Этим методом пользуются на практике для определения эффективного коэффициента отражения. Для этого, изменяя высоту передающей и приемной антенн, ведут измерение |R| в широком диапазоне углов падения волны.

Если распространение радиоволн происходит над неоднородной поверхностью, то, прежде чем рассчитывать напряженность поля, следует определить положение и размеры отражающей области. Так, например, если отражающая область попадает на ограниченную водную поверхность (озеро), тогда как передающий и приемный пункты находятся на суше на сравнительно большом удалении от берега, то при расчете напряженности поля следует пользоваться коэффициентами отражения от водной поверхности, т. е. характер поля будет такой, как если бы вся трасса проходила над водой.

Радиолокационные отражения от земной поверхности

Отражения от неровной земной поверхности носят рассеянный характер, причем часть отраженной мощности оказывается направленной к источнику. Эта мощность создает так называемое обратное отражение. Обратные отражения чаще всего относятся к мешающим сигналам, которые затрудняют распознавание полезных радиолокационных целей. Однако отражения от земной поверхности к источнику используют при проведении наблюдений за поверхностью Земли с воздуха, например, при высотометрии. Для оценки интенсивности обратных отражений, создаваемых различными видами неровной земной поверхности, вводят понятие эффективной отражающей площади. Эффективной отражающей площадью называется фиктивная поверхность, являющаяся изотропным и не поглощающим мощность переизлучателем, которая, будучи совмещена с реальной поверхностью, создает у антенны радиолокатора такую же плотность потока мощности отраженного сигнала, как и реальная поверхность [23]:

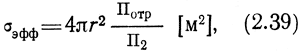
где П_отр - плотность потока мощности, переизлученного отражающей поверхностью и созданного вблизи излучателя; П₂ - плотность потока мощности, созданного излучателем вблизи отражающей поверхности.

Величина σ_эфф зависит от угла падения волны на поверхность, крутизны неровностей поверхности, комплексной диэлектрической проницаемости и несущей частоты. Средняя удельная эффективная отражающая площадь σ_эфф.уд характеризует отражающие свойства единицы площади поверхности и является безразмерной величиной:

где S - площадь поверхности, формирующая отраженный сигнал.

Площадь S определяется при узких диаграммах направленности шириной диаграммы направленности, при широких диаграммах направленности - размером первой зоны Френеля при отражении. Кроме того, величина S зависит от параметров радиолокационной станции.

Зависимость σ_эфф.уд. от угла падения волны на поверхность называют диаграммой обратного рассеяния поверхности (ДОР). Часто пользуются понятием нормированной ДОР, представляющей собой зависимость отношения σ_эфф.уд. / σ_{эфф.уд.о}, от угла падения, где σ_{эфф.уд.о} - удельная эффективная отражающая площадь при нормальном падении волны на поверхность. Величины σ_эфф.уд. и виды ДОР снимают экспериментально. На рис. 2.22 приведены результаты таких измерений для отражения радиоволн длиной λ = 0,86 см и λ = 3,2 см от морской поверхности при различных скоростях ветра [22]. Из графиков видно, что с укорочением длины волны величина σ_эфф.уд. растет при всех углах падения волны, т. е. большая часть энергии рассеивается в обратном направлении. Чем сильнее ветер, тем шире ДОР, следовательно, интенсивность обратных отражений при наклонном падении волны возрастает с увеличением неровностей поверхности. Таким образом, величина σ_эфф.уд. возрастает с увеличением отношения высоты неровности к длине волны.

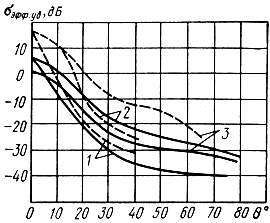
Рис. 2.22. Зависимость удельной эффективной отражающей площади σ_эфф.уд морской поверхности от угла падения волны при различных длинах радиоволн и скоростях ветра: --- λ = 0,86 см; ^___ λ = 3,2 см; 1 - скорость ветра 9÷19 км/ч; 2 - скорость ветра 19÷28 км/ч; 3 - скорость ветра 37 км/ч

Мощность на входе согласованной приемной антенны радиолокатора вычисляют следующим образом. Плотность потока мощности, созданного излучателем вблизи отражающей поверхности, определяется из (1.14):

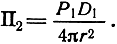
Плотность потока мощности, переизлученного отражающей поверхностью и созданного вблизи излучателя,

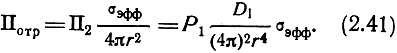
Мощность в приемной антенне радиолокатора с учетом (2.41) и (1.13) определяется выражением

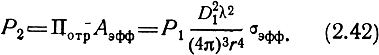
Мощность в приемной антенне радиолокатора прямо пропорциональна величине σ_эфф и обратно пропорциональна четвертой степени расстояния до поверхности или цели.

Трасса, проходящая над пологими холмами

На рис. 2.23, а изображен профиль трассы, при котором передающая антенна расположена на пологом склоне холма. В этом случае к приемной антенне В могут прийти прямой луч АВ и три отраженных луча АС₁В, АС₂В и AC₃C₃'B. При расчете напряженности электрического поля следует учитывать разность фаз этих лучей, обусловленную разностью хода и разными условиями отражения в точках С₁, С₂ и С₃. В результате рассмотрения такой картины можно получить выражение для расчета напряженности поля, аналогичное интерференционным формулам (2.10) или (2.20), но более сложное.

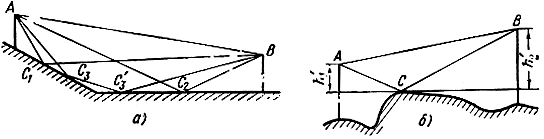
Рис. 2.23. Распространение УКВ в пересеченной местности: а - передающая антенна расположена на пологом склоне холма; б - в середине трассы имеется возвышенность

Если передающая и приемная антенны помещаются на пологих склонах холма, то при определенном соотношении высот передающей и приемной антенн поле в точке приема окажется результатом интерференции восьми лучей, приходящих различными путями. Понятно, что при этом расчет напряженности электрического поля еще более усложняется.

На рис. 2.23, б изображен профиль, при котором имеется возвышенность в середине трассы. В простейшем случае в точку В приходит только один луч, отражающийся в точке С. Для расчета такой трассы удобно ввести понятие приведенных высот h₁' и h₂' антенн и свести задачу к распространению радиоволн над фиктивной; плоскостью, касательной к поверхности Земли в точке отражения. При наличии нескольких отраженных лучей задача усложняется.

Когда на пути распространения волны встречается много препятствий, различных по форме и размеру, расчет напряженности электрического поля практически невозможен.

На рис. 2.24 изображено изменение напряженности электрического поля с расстоянием над трассой сложного профиля.

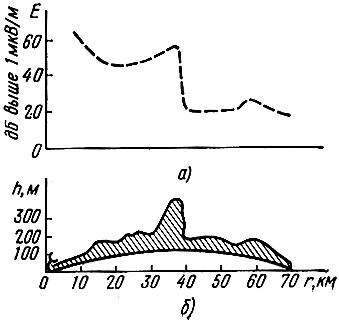
Рис. 2.24. Результаты измерения напряженности электрического поля на волне 0,5 м над неровной местностью: а - график напряженности поля; б - профиль трассы

Из рисунка видно, что с приближением к вершине холма напряженность поля возрастает, а за холмом - резко убывает.

Трасса, проходящая над высоким холмом или горным кряжем

Для приближенного расчета напряженности поля на трассе, проходящей над высоким холмом или горным кряжем, можно воспользоваться теорией дифракции электромагнитных волн на непрозрачном клиновидном экране (см. § 1.3). В этом случае напряженность поля за препятствием определяют, умножая напряженность поля в свободном пространстве на множитель ослабления Е/Е₀ (см. рис. 1.6, в). Анализ формулы (1.26) и графика рис. 1.6, в позволяет проследить зависимость величины напряженности поля от длины волны, высоты препятствия и расстояния за препятствием. Видно, что непосредственно за препятствием имеется область тени, а затем на некотором отрезке пути наблюдается возрастание напряженности поля.

На трассах УКВ протяженностью примерно 100÷150 км, проходящих через горные кряжи высотой 1000÷2000 м, наблюдается явление, называемое усилением препятствием. Это явление заключается в том, что интенсивность электромагнитного поля радиоволны при некотором удалении от препятствия может оказаться дольше, чем на том же расстоянии от передатчика на трассе без препятствия. Схема трассы с "усиливающим" препятствием изображена на рис. 2.25.

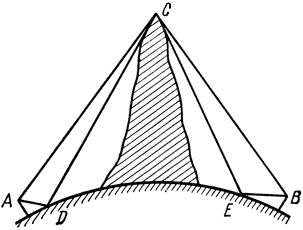
Рис. 2.25. Схема трассы с 'усиливающим' препятствием

Физика явления "усиления препятствием" заключается в том, что вершина горы служит естественным ретранслятором. Поле, возбуждающее вершину горы, складывается из двух волн - прямой АС и отраженной ADC. Волны дифрагируют на острой вершине горы, как на клиновидном препятствии, и распространяются в область за гору. При этом в место расположения приемной антенны В придут два луча - СЕВ и СВ. Таким образом, на участках трассы передатчик - гора и гора - приемник распространение идет в пределах расстояния прямой видимости.

При отсутствии препятствия расстояние 100÷150 км намного превышает расстояние прямой видимости, и в месте приема имеется весьма слабое поле, обусловленное дифракцией на сферической поверхности Земли. Расчеты и эксперименты показывают, что такое препятствие-ретранслятор может дать усиление напряженности электрического поля 60÷80 дБ.

Исследования, проведенные на трассах, пересекающих хребты, показали, что использование явления "усиления препятствием" экономически выгодно: оно избавляет от необходимости устанавливать высокогорные ретрансляционные станции [28].

Распространение УКВ в пределах большого города

Большой город с точки зрения распространения радиоволн можно рассматривать как сильно пересеченную местность. Расчет напряженности электрического поля в таких условиях практически невозможен. Многочисленные опыты показали, что в среднем напряженность поля УКВ в городе меньше, чем на открытой местности, примерно в 3÷5 раз. Поэтому грубую оценку среднего уровня напряженности поля можно производить по формуле Введенского (2.29), вводя в нее множитель (0,2÷0,4).

Если имеется прямая видимость между передающей и приемной антеннами, то расчет можно вести по формуле Введенского, причем высоту расположения антенн следует отсчитывать от среднего уровня крыш.

Внутри помещений структура поля является еще более сложной. При расчете напряженности поля внутри помещения необходимо учитывать поглощение УКВ в стенах здания согласно формуле (1.41).