§ 2.10. Распространение радиоволн над неровной или неоднородной трассой, когда антенны расположены низко над поверхностью Земли

На распространение средних и длинных радиоволн, на которых в основном применяются антенны, расположенные низко над поверхностью Земли, влияние неровностей земной поверхности оказывается меньше, чем на более коротких волнах [см. формулу (2.37)].

Сопоставление расчетов с результатами измерений показало, что учет влияния рельефа местности в этом случае можно проводить, заменяя в формулах для гладкой поверхности Земли (2.53) и (2.54) проводимость γ₂ на эффективную проводимость γ_2эфф. Величина γ_2эфф определяется усредненными электрическими параметрами почвы на трассе и рельефом местности. С увеличением отношения высоты неровности к длине волны величина γ_2эфф уменьшается. Приближенно считают, что на средних волнах для равнинной местности γ_2эфф = 0,5γ₂, а для холмистой местности у_2эфф = (0,1÷0,2)γ2 [8].

Теория и практика показывают, что при использовании антенн, расположенных вблизи земной поверхности, наибольшее влияние на распространение радиоволн оказывают участки, находящиеся в непосредственной близости от передающей и приемной антенн [6].

Формулы для расчета напряженности электрического поля над неоднородной трассой учитывают самые простые случаи - трассы, состоящие из двух или трех однородных участков.

Наибольший интерес представляет случай резкого изменения электрических параметров среды, который имеет место при переходе трассы с суши на море. Если модуль комплексной диэлектрической проницаемости сухопутного участка много больше единицы, как это обычно бывает на длинных и средних волнах, то применимы граничные условия Леонтовича. Е. Л. Фейнберг получил следующую формулу для расчета коэффициента ослабления в этих условиях [6]:

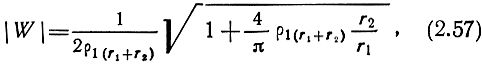
где ρ₁(r₁ + r₂) - численное расстояние, определяемое по формуле (2.54); при расчете берут электрические параметры сухопутного участка, а за расстояние принимают полную длину трассы r = r₁ + r₂.

Если напряженность поля определяется над сушей на значительном расстоянии от излучателя, то множитель ослабления

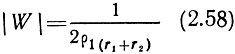
При определении напряженности поля над морем на небольшом расстоянии от берега множитель ослабления определяется выражением (2.57). В рассматриваемых условиях возможно увеличение напряженности поля с удалением от передатчика. Небольшое удаление от береговой линии приводит к росту напряженности поля, тем большему, чем хуже электропроводность участка суши.

Е. Л. Фейнбергом получены формулы и проведены расчеты для определения множителя ослабления над трассой, состоящей из трех участков: суша - море - суша и море - суша - море.

На рис. 2.30 изображен график изменения напряженности электрического поля над трассой, состоящей из трех участков. На рис. 2.30 концевыми участками трассы является море, а на рис. 2.31 - суша.

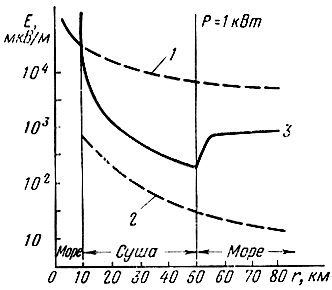
Рис. 2.30. Изменение напряженности поля с расстоянием над трассой море - суша - море: 1 - однородная морская трасса; 2 - однородная сухопутная трасса; 3 - трасса море - суша - море

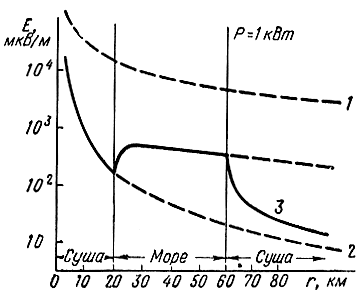
Рис. 2.31. Изменение напряженности поля с расстоянием над трассой суша - море - суша: 1 - однородная морская трасса; 2 - однородная сухопутная трасса; 3 - трасса суша - море - суша

В первом случае напряженность поля близка к напряженности поля на однородной морской трассе, во втором случае - на однородной сухопутной трассе. Таким образом, в обоих случаях основное влияние на величину напряженности поля оказывают концевые участки трассы. На графиках видно увеличение напряженности поля при переходе с суши на море.

Еще нагляднее влияние концевых участков трассы видно на графике рис. 2.32, где представлена зависимость множителя ослабления от коэффициента заполнения трассы сушей.

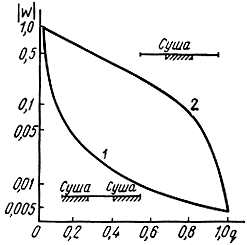
Рис. 2.32. Зависимость множителя ослабления от коэффициента заполнения трассы сушей: 1 - суша - море - суша; 2 - море - суша - море

Коэффициентом заполнения трассы сушей называется отношение протяженности трассы, проходящей над сушей, к протяженности всей трассы:

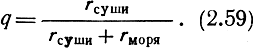
Если концевые участки трассы находятся на суше, то даже при небольшой протяженности этих участков (q = 0,1) множитель ослабления так же мал, как на полностью сухопутной трассе. Если концевые участки трассы находятся на море, то влияние суши сказывается только при коэффициенте заполнения сушей q = 0,9.

Для работы радионавигационных устройств и радиодальномеров необходимо знать точное значение скорости распространения земных радиоволн. Исследование вопроса о скорости распространения было проведено П. А. Рязиным в 1950 г. [6].

Из строгой теории следует, что множитель ослабления является комплексной величиной и мгновенное значение напряженности поля на некотором расстоянии от излучателя

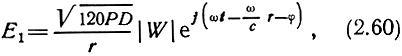
где φ - фазовый угол, являющийся функцией численного расстояния ρ.

Изменение фазы волны с расстоянием эквивалентно изменению фазовой скорости. Действительно, приравнивая полный дифференциал фазы нулю:

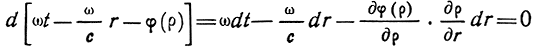
и подставляя значение ρ из (2.54), находим фазовую скорость

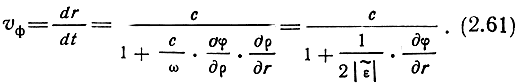
На рис. 2.33 построен график зависимости фазовой скорости поверхностной волны от параметра ρ, рассчитанный П. А. Рязиным.

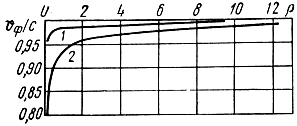
Рис. 2.33. Зависимость фазовой скорости поверхностной волны от параметра ρ: 1 - морская трасса; 2 - сухопутная трасса

Из кривых видно, что при малых значениях ρ фазовая скорость поверхностной волны меньше скорости света и практически равна скорости света при ρ > 20. Чем больше электропроводность и диэлектрическая проницаемость поверхности, тем быстрее фазовая скорость приближается к скорости света. Условие равенства фазовой скорости и скорости света можно считать выполненным, начиная с расстояний в несколько десятков длин волн.

Эксперименты, проведенные под руководством советских ученых Л. И. Мандельштама и Н. Д. Папалекси, подтвердили результаты расчетов.

Анализ зависимости фазовой скорости поверхностной волны от электрических свойств земной поверхности позволил решить вопрос, важный для радионавигации, - разработать метод расчета ошибок береговой рефракции. Явление береговой рефракции заключается в следующем. Пусть, как это изображено на рис. 2,34, передатчик находится на море в точке А, а приемник - на суше в точке О.

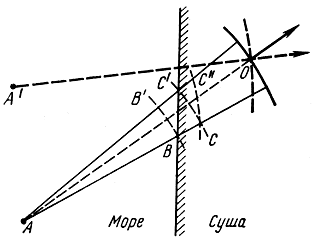
Рис. 2.34. К пояснению явления береговой рефракции

Над морем волна распространяется с фазовой скоростью, равной скорости света. В точках В и В′ фазы волны равны. Над сушей волна распространяется с меньшей скоростью, поэтому на дуге окружности СС′ фаза волны в точке С отстает от фазы волны в точке С′ и линией равных фаз является дуга СС″.

За направление прихода волны принимается нормаль к фронту волны, т. е. направление А′О, которое не совпадает с действительным направлением на передатчик. Угол между действительным и кажущимся направлением на передатчик А′ОА является углом рефракционной ошибки.

Для расчета рефракционных ошибок составлены графики и номограммы [6]. Следует обратить внимание на то, что при береговой рефракции угол преломления поверхностной волны меньше угла падения. Ошибка уменьшается с улучшением электропроводности почвы. Наибольшая ошибка имеет место вблизи берега. С удалением от береговой линии рефракционная ошибка уменьшается.