§ 2.11. Расчет напряженности электрического поля в зоне тени (дифракции)

В начале развития радиотехники, когда не было известно о существовании ионосферы, делались попытки объяснить проникновение радиоволн за пределы прямой видимости только дифракцией. Решение задачи распространения земной волны вблизи полупроводящей сферы оказалось весьма сложным. Необходимо было решить волновое уравнение в сферической системе координат. Решение в пригодной для расчетов форме было получено Г. Ватсоном в 1918 г. для хорошо проводящей поверхности (60γλ >> ε). Над усовершенствованием этого решения работали Т. Эккерслей, Б. А. Введенский, Б. Ван-дер-Поль, которыми были получены формулы для определения напряженности электрического поля на больших расстояниях от передатчика.

С развитием техники УКВ распространение ультракоротких волн за пределы прямой видимости также пытались объяснить дифракцией. Позднее было установлено, что сравнительно высокие значения напряженности электрического поля обусловлены влиянием тропосферы на распространение УКВ.

В 1945 г. советский ученый В. А. Фок получил общее выражение для напряженности электрического поля в месте приема, пригодное для любых расстояний от передатчика. Однако определение напряженности поля по формуле Фока связано со сложными вычислениями, поскольку эта формула представляет собой ряд, плохо сходящийся при небольших расстояниях от передатчика [6].

Для значительных расстояний, в области тени, когда выпуклость Земли экранирует точку приема, можно учитывать только первый член ряда и рассчитывать напряженность поля по формуле

где Е_0m определяется по формуле (1.8); F - множитель ослабления.

Множитель ослабления является произведением трех функций:

или

Здесь U(х) - функция, зависящая от расстояния и электрических параметров почвы; V(y₁), V(y₂) - функции, зависящие от подъема передающей и приемной антенн. Параметры х, у₁, у₂ определяются следующими выражениями:

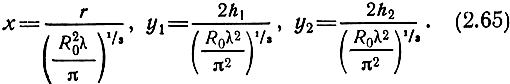
Для определения функций U и V по подсчитанным параметрам х, у₁, у₂ существуют графики, приведенные на рис. 2.35 и 2.36.

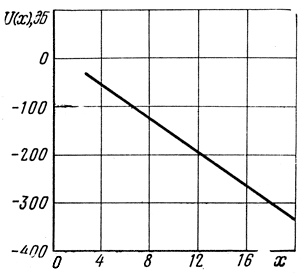
Рис. 2.35. График для определения функции ослабления U(x)

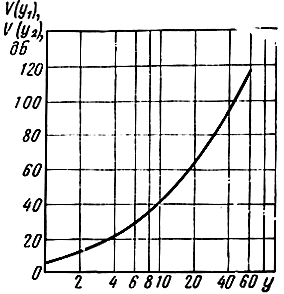
Рис. 2.36. График для определения функции высоты подъема антенн V(y)

Расчет по этим графикам проводится главным образом для диапазона УКВ, где применяются антенны, высоко поднятые над поверхностью Земли. Расчет напряженности поля в диапазонах длинных, средних и даже коротких волн, когда антенны располагаются вблизи Земли, упрощается, поскольку V(y₁) = V(y₂) = 1.

Для определения напряженности поля в зоне дифракции при антеннах, расположенных вблизи Земли, служат графики Международного консультативного комитета по радиосвязи (МККР), построенные на основании расчетов по дифракционным формулам (рис. 2.37).

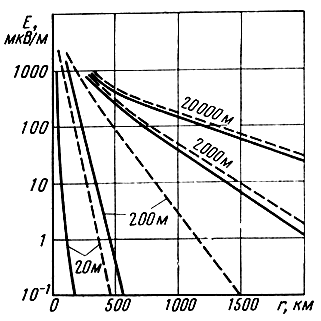
Рис. 2.37. Графики МККР для определения напряженности поля в зоне дифракции

На графиках приведена зависимость напряженности поля от расстояния для различных длин волн и различных электрических параметров земной (поверхности при мощности передатчика 1 кВт. Чтобы определить напряженность поля при заданной мощности передатчика, необходимо значение напряженности поля, определенное по графику, умножить на величину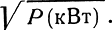  

Из графиков видно, что напряженность поля в зоне дифракции убывает с расстоянием по экспоненциальному закону, т. е. гораздо быстрее, чем при распространений воли над плоской земной поверхностью. Поэтому напряженность поля в зоне дифракции значительно ослаблена. Напряженность поля тем больше, чем длиннее волна, так как с увеличением длины волны уменьшается, во-первых, влияние препятствия - сферичности Земли, и во-вторых, поглощение волн в полупроводящей поверхности Земли.

Контрольные вопросы к главе 2

1. Каковы средние значения проводимости суши и моря?

2. В каком диапазоне радиоволн плотность токов смещения в земной поверхности преобладает над плотностью токов проводимости?

3. Выведите соотношение, связывающее фазовую скорость распространения волны υ_ф с коэффициентом фазы β в полупроводящей среде. Какой вид принимает это соотношение для диапазона УКВ?

4. Плоские волны частотой 500 и 5 МГц проходят во влажной почве расстояние 10 м. Во сколько раз изменятся амплитуды той и другой волн? Как изменятся фазы волн?

5. Во сколько раз изменится коэффициент отражения горизонтально-поляризованных волн длиной 30 см и 30 м при нормальном падении их (θ = 0) на сухую поверхность и на болотистую почву?

6. Определите изменение амплитуды и фазы вертикально-поляризованной плоской волны длиной 10 см при отражении ее от влажной почвы под углом 60° на высоте 10 м от поверхности Земли по сравнению с амплитудой и фазой падающей волны вблизи поверхности.

7. В чем заключается явление полного отражения и при каких условиях оно может иметь место?

8. Где и во сколько раз больше расстояние прямой видимости - на Земле или на Луне при одних и тех же высотах поднятия антенн h₁ = 12 м, h₂ = 1 м.

Радиус Земли 6370 км, радиус Луны 1738 км.

9. Назовите условия применимости интерференционной формулы. В каком диапазоне радиоволн расчет напряженности поля ведут по этой формуле?

10. Нарисуйте диаграммы направленности вертикального и горизонтального вибраторов, поднятых на высоту h₁ = 2λ над сухой почвой.

11. Как изменится диаграмма направленности в случае, указанном в вопросе 10, при укорочении длины волны вдвое (высота h₁ та же)?

12. Как изменится диаграмма направленности в случае, указанном в вопросе 10, при увеличении электропроводности почвы?

13. Какой участок земной поверхности оказывает существенное влияние на распространение радиоволн, если антенны подняты высоко над поверхностью Земли?

14. При каких условиях можно вести расчет напряженности поля по формуле Введенского?

15. Чем объясняется квадратичная зависимость напряженности поля от расстояния в условиях применимости формулы Введенского?

16. Можно ли считать поверхность Земли ровной, если высота неровностей 16 см, длина падающей волны 8 см, угол падения 60°?

17. Какие составляющие имеет поле Вертикального вибратора, расположенного вблизи полупроводящей поверхности Земли?

18. Каково соотношение между горизонтальными составляющими электрического поля волн, распространяющихся над влажной землей и над морем, при λ = 500 м, если предположить, что вертикальные составляющие равны?

19. Как изменится напряженность поля, созданного вертикальным вибратором, расположенным вблизи земной поверхности, при изменении длины волны с 20 до 200 м? Поверхность Земли - влажная почва.

20. В каких диапазонах волн применяются антенны типа заземленного вибратора?

21. В каком диапазоне волн существенно сказываются ошибки в определении координат излучателя, вызванные береговой рефракцией?