§ 4.13. Распространение радиоволн в направлении, перпендикулярном к направлению постоянного магнитного поля

Рассмотрим распространение волны в направлении, перпендикулярном к направлению постоянного магнитного поля. Пусть волна распространяется вдоль оси z, а магнитное поле направлено вдоль отрицательных значений оси у (рис. 4.17).

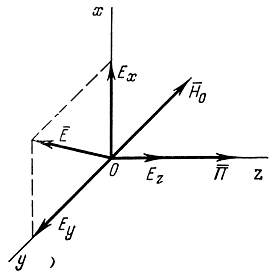
Рис. 4.17. Распространение радиоволн в направлении, перпендикулярном к направлению постоянного магнитного поля

В этом случае вектор E^- лежит в плоскости хОу и имеет составляющую Ех, нормальную к направлению магнитного поля, и составляющую Еу, совпадающую с направлением магнитного поля.

Очевидно, на электрон, получающий скорость под действием составляющей поля Е_У, магнитное поле не действует, поскольку сила Лоренца равна нулю. Следовательно, распространение волны происходит так же, как в отсутствие магнитного поля, и величина ε определяется выражением (4.8).

На электрон, получающий скорость под действием составляющей поля Е_х, действует сила Лоренца, направленная по оси z:

Обратимся снова к уравнению движения электрона (4.71) и определим координатные составляющие вектора поляризации единицы объема ионизированного газа р^-_э:

Скалярные уравнения будут иметь вид

Кроме того, из третьего уравнения Максвелла следует, что в направлении распространения плоской волны D = 0 [1]. Это значит, что в нашем случае

откуда

Подставляя уравнение (4.91) в выражение (4.88), определяем p_z:

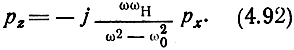
Используя формулы (4.89) и (4.92), получаем

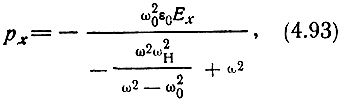
откуда

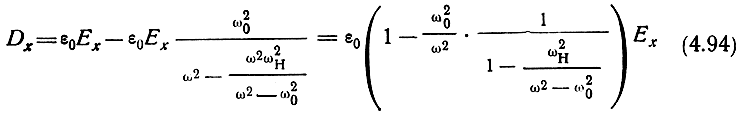
и, следовательно,

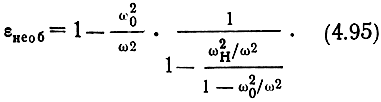
Из уравнения (4.91) следует, что имеется составляющая поля в направлении распространения волны E_z. Величину Е_z можно определить, подставив выражения (4.92) и (4.93) в (4.91):

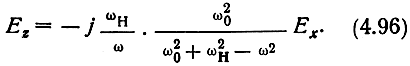
Из рассмотренного видно, что волна, распространяющаяся нормально к силовым линиям постоянного магнитного поля, распадается на две составляющие.

Вектор Е‾ первой составляющей волны совпадает по направлению с линиями постоянного магнитного поля, и магнитное поле не влияет на распространение этой составляющей волны. Такая волна называется обыкновенной.

Вектор Е‾ второй составляющей волны нормален к силовым линиям постоянного магнитного поля. Эта волна распространяется с фазовой скоростью, определяемой диэлектрической проницаемостью по формуле (4.95). При этом появляется составляющая напряженности поля вдоль направления распространения, не совпадающая по фазе с поперечной составляющей, и поле оказывается эллиптически поляризованным в плоскости распространения волны. Такая волна называется необыкновенной.

График зависимости относительных диэлектрических проницаемостей обыкновенной и необыкновенной волн от отношения ω₀²/ω² представлены на рис. 4.18.

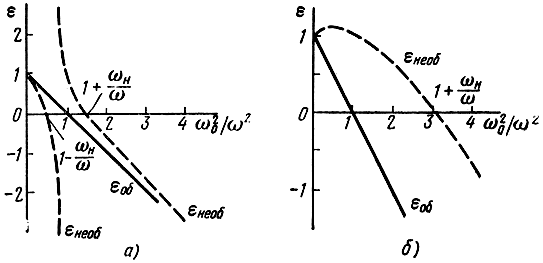
Рис. 4.18. Зависимость относительной диэлектрической проницаемости волны, распространяющейся в направлении, перпендикулярном к направлению постоянного магнитного поля от отношения (ω₀²/ω²: а - отношение ω_H/ω = ¹/₂; б - отношение ω_H/ω = 2

Относительная диэлектрическая проницаемость обыкновенной волны равна нулю при ω₀²/ω² = 1. Относительная диэлектрическая проницаемость необыкновенной волны обращается в нуль при двух значениях ω₀²/ω², если ω_H/ω < 1 (рис. 4.18, а). Действительно, из уравнения (4.95) следует, что при ε_необ = 0

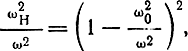
откуда

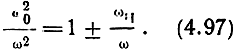
Составляющие обыкновенной и необыкновенной воли претерпевают при распространении различное поглощение (в условиях ионосферы больше поглощается составляющая необыкновенной волны).