
§ 4.12. Распространение радиоволн в направлении постоянного магнитного поля
Получим выражение для диэлектрической проницаемости ионизированного газа в случае, когда направление распространения волны совпадает с направлением постоянного магнитного поля. Ориентируем ось z декартовой системы координат в этом же направлении (рис. 4.15).
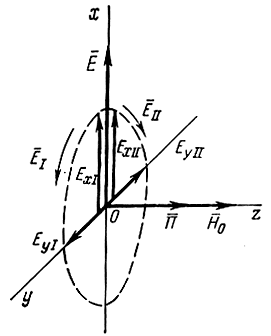
Рис. 4.15. Распространение радиоволн в направлении постоянного магнитного поля
При этом вектор E‾ распространяющейся волны лежит в плоскости хОy и, не нарушая общности, можно ориентировать ось х в направлении вектора Е‾.
Величину диэлектрической проницаемости ионизированного газа в присутствии магнитного поля будем определять, используя уравнение (3.4).
Выше было установлено, что при отсутствии электромагнитной волны электрон движется по окружности в плоскости, нормальной к направлению постоянного магнитного поля.
Для рассмотрения процессов, происходящих при распространении волны, удобно разложить линейно-поляризованную волну на две волны с круговой поляризацией и разным направлением вращения векторов Е‾.
Составляющие волны запишутся в следующем виде:
с вращением вектора Е‾I по часовой стрелке
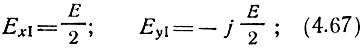
с вращением вектора Е‾II против часовой стрелки
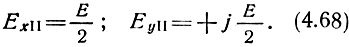
Если для проверки сложить составляющие этих волн по осям х и у, то получим вектор Е‾ в направлении оси х.
Направление вращения вектора E‾I и направление вращения электрона в постоянном магнитном поле совпадают. Смещения электрона под действием волны и постоянного магнитного поля суммируются.
Волна с электрическим полем Е‾II сообщает электрону смещение в направлении, противоположном направлению вращения электрона в постоянном магнитном поле, и результирующее смещение электрона является разностью этих смещений. Следовательно, смещение, получаемое электроном под Действием полей E‾I и Е‾II, различно. Ионизированный газ поляризуется по-разному волнами с правым и левым вращением вектора E‾. Поскольку поляризация определяет диэлектрическую проницаемость вещества, последняя оказывается разной для этих двух волн. Таким образом, при распространении волны в направлении постоянного магнитного поля линейно-поляризованная волна распадается на две волны, поляризованные по кругу с противоположным направлением вращения вектора Е‾, причем диэлектрическая проницаемость среды для этих волн различна.
Получим выражения для диэлектрической проницаемости каждой из этих волн.
Для этого из уравнения движения электрона (4.65) определим вектор поляризации р‾э.
Рассматриваются гармонические колебания, величина вектора Е‾ меняется гармонически и смещение электрона l‾э меняется также по гармоническому закону. Подставив в выражение (4.65) значение первой и второй производных l‾э по времени [см. уравнение (4.13)], получим
- mэω2l‾э = - еE‾ - jеμ0ω[l‾эН‾0]. (4.69)
Умножая обе части равенства (4.69) на 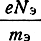
и учитывая уравнение (4.66), получим
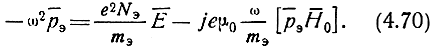
Используя обозначения 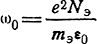
и 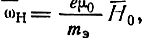
перепишем уравнение (4.70) в виде
- ω2p‾э = ω‾20ε0E‾ - jω[p‾эω‾Н]. (4.71)
Векторное уравнение (4.71) можно представить в виде системы алгебраических уравнений, которая для рассматриваемого случая запишется так:
- ω2p‾эх = ω‾20ε0Eх - jωp‾эyωН; (4.72)
- ω2p‾эy = ω‾20ε0Ey + jωp‾эxωН. (4.73)
Определяя из уравнения (4.73) рэ у и подставляя его значения в (4.72), получим выражение для рэ х:
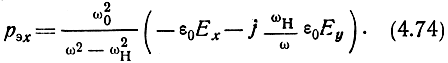
Подставляя уравнение (4.74) в (4.73), определяем рэу:
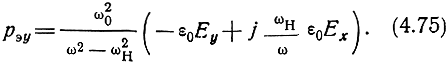
Учитывая, что для волны с вращением вектора Е‾ по часовой стрелке составляющие вектора Е‾ по координатным осям определяются выражениями (4.67), перепишем формулы (4.74) и (4.75) в следующем виде:
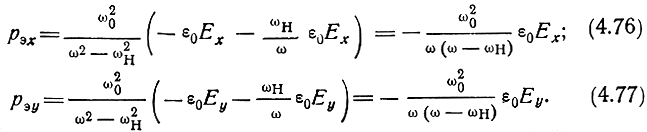
В соответствии с уравнением (3.4) составляющие вектора электрического смещения определяются так:
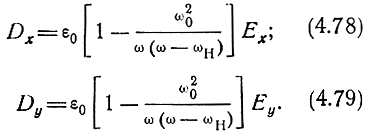
Сопоставляя полученные выражения с уравнением (3.4), видим, что относительная диэлектрическая проницаемость для составляющей волны с вращением вектора Е‾ по часовой стрелке
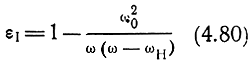
или
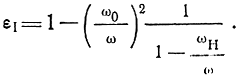
Выражение для относительной диэлектрической проницаемости составляющей волны с вращением вектора Е‾ против часовой стрелки получим, подставляя в уравнения (4.74) и (4.75) значения Е из (4.68) и затем переходя к выражениям для D:
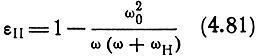
или
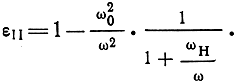
Рассмотрим зависимости диэлектрической проницаемости ионизированного газа от ω, ω0 и ωН при распространении волны в направлении постоянного магнитного поля и выясним физические явления, возникающие в процессе распространения волны.
На рис. 4.16 представлен график зависимости относительных диэлектрических проницаемостей εI и εII от отношения ω02/ω2.
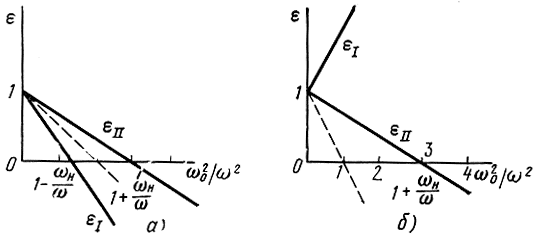
Рис. 4.16 Зависимость относительной диэлектрической проницаемости волны, распространяющейся направлении постоянного магнитного поля от отношения ω02/ω2: а - отношение ωН/ω = 1/2; б - отношение ωН/ω = 2
В такой системе координат график имеет вид прямой. Здесь же пунктиром нанесен график зависимости ε от ω02/ω2 при H0 = 0. В этом случае ε = 0, при ω02/ω2 = 1. Если имеется постоянное магнитное поле и ωН/ω < 1, то εI = 0 при ω02/ω2 = 1 - ωH/ω, а εII = 0 при ω02/ω = 1 + ωH/ω (рис. 4.16, а). Волна с составляющей поля ЕII может распространяться в ионизированном газе большей электронной плотности, чем волна поля составляющей EI или волна в отсутствие магнитного поля.
С другой стороны, если ωН/ω > 1 (рис. 4.16, б), то, как следует из уравнения (4.80), значение εI положительно при любом отношении ω0/ω и в ионизированном газе могут распространяться волны очень низких частот с составляющей EI.
Для выяснения возможности распространения радиоволн в ионизированном газе при ω02 > ω2 в направлении постоянного магнитного поля рассмотрим зависимость е от отношения ωН/ω.
Из выражений (4.80) и (4.81) видно, что диэлектрическая проницаемость εI для волны с составляющей поля EI положительна при ωН/ω > 1, диэлектрическая проницаемость εII для волны с составляющей поля ЕII становится положительной при ωН/ω > (ω02/ω2 - 1), т. е. при большем значении постоянного магнитного поля (если ω02/ω2 > 2).
В природе наблюдается явление прохождения через ионизированный газ волны, частота которой ниже собственной частоты ионизированного газа (ω < ω0) в присутствии постоянного магнитного поля. Так, при определенных условиях сверхдлинные волны могут проходить сквозь толщу ионосферы, не отражаясь от слоя F (см. гл. 5). Это же явление используют в некоторых случаях, когда необходимо обеспечить прохождение волн через плотный слой ионизированного газа.
При распространении радиоволн в направлении постоянного магнитного поля происходит поворот плоскости поляризации распространяющейся волны.
Как указывалось, распространяющаяся волна распадается на две волны, поляризованные по кругу в разных направлениях и имеющие разные фазовые скорости.
Через некоторое расстояние r, которое эти волны пройдут вдоль линий постоянного магнитного поля, проекции векторов Е- на координатные оси запишутся так:
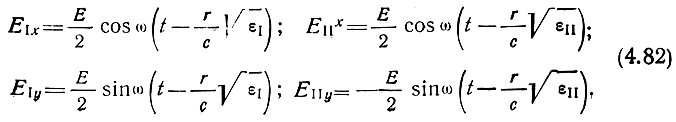
Результирующее колебание, получающееся путем суммирование составляющих поля по осям, запишется в виде
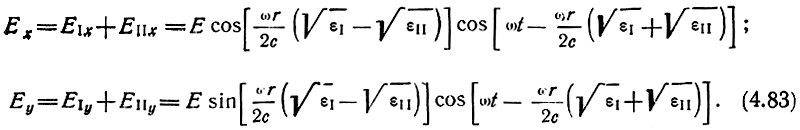
В начале координат поле было направлено по оси х. После прохождения волной расстояния r появились две синфазные составляющие поля. Поэтому в сумме они дают линейно-поляризованное колебание, плоскость поляризации которого повернута относительно оси х на угол ψ.
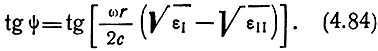
Для достаточно высоких частот √ε можно вычислить приближенно:
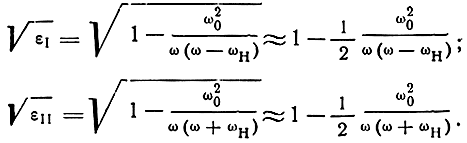
Угол поворота плоскости поляризации приближенно равен
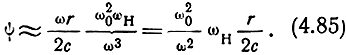
Составляющие волны, векторы которых E-I и Е-II имеют разное направление вращения, испытывают в ионизированном газе в присутствии постоянного магнитного поля различное поглощение, что приводит к появлению эллиптической поляризации результирующего колебания. При распространении волны происходит поворот большой оси эллипса и расширение эллипса за счет более интенсивного поглощения одной из составляющих волн. В пределе эллиптическая поляризация может перейти в круговую.

© RATELI.RU, 2010-2020
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
