§ 4.18. Теоремы эквивалентности

Ионосферные станции определяют действующие высоты отражения радиоволн и максимальные частоты отражения при вертикальном падении волны на ионосферу. Понятно, что для целей радиосвязи используют волны, посланные под некоторым углом θ ≠ 0 к поверхности ионизированных слоев. Необходимо установить соотношения между условиями отражения при вертикальном и наклонном падении волны на ионосферу.

В предположении плоской ионосферы, что справедливо для сравнительно небольших расстояний, эти соотношения определяются двумя теоремами эквивалентности. С учетом сферической формы Земли соотношения приобретают более сложный вид.

Согласно первой теореме эквивалентности, если высоты отражения волн, посланных вертикально и наклонно к ионосфере, равны, то и действующие высоты отражения этих волн равны.

На рис. 4.27 схематически представлено соотношение действующей высоты z_д и высоты отражения z₀, отсчитываемых от высоты h₀. Обозначая через r расстояние AD, определим действующую высоту отражения при наклонном падении волны

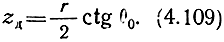
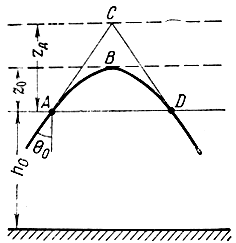
Рис. 4.27. К доказательству теоремы эквивалентности

С другой стороны, расстояние r можно определить как интеграл проекций элементарных отрезков кривой ABD на прямую AD:

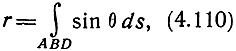
где ds - элемент криволинейной траектории волны; θ - переменный угол, составляемый этим элементом с вертикалью.

Используя закон преломления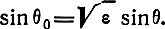  
подставляя (4.110) в (4.109) и переходя от переменной s к z, получим

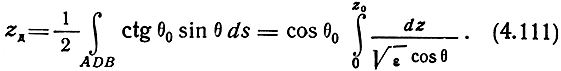
Знаменатель последнего выражения можно преобразовать:

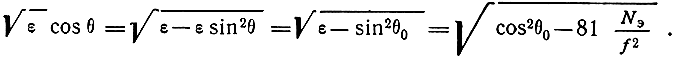
Далее, используя соотношение между частотами радиоволн, отражающихся при вертикальном и наклонном падении на ионосферу, получим

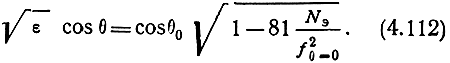
Подставляя (4.112) в (4.111), найдем выражение для действующей высоты отражения волны при наклонном падении:

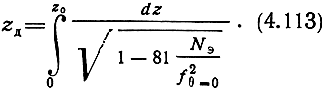
Последнее выражение совпадает с (4.108). Следовательно, действующие высоты отражения волн при вертикальном и наклонном падении равны.

Согласно второй теореме эквивалентности, время, затрачиваемое радиоволной на прохождение криволинейного пути в ионосфере, равно времени, которое затратила бы волна, распространяющаяся со скоростью света в свободном пространстве по эквивалентному треугольному пути.

Время, затрачиваемое волной на прохождение криволинейного пути, равно

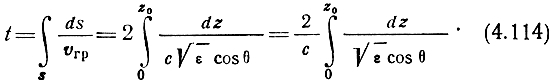
Сравнивая выражения (4.114) и (4.111), можно записать

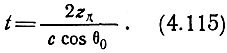
Эквивалентный треугольный путь волна проходит со скоростью света с за время

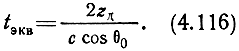
Поскольку правые части выражений (4.115) и (4.116) равны, можно записать

Используя приведенные выше теоремы, можно рассматривать не криволинейный путь волны в ионосфере, а эквивалентный треугольный путь, что существенно упрощает расчеты.