§ 8.5. Ошибки, вносимые атмосферой Земли в определение угловых координат космических кораблей и спутников радиотехническими методами

Как указывалось, прохождение радиоволн в тропосфере и ионосфере сопровождается искривлением их траектории - рефракцией.

При определении угловых координат космического объекта радиотехническими методами вследствие рефракции направление прихода волны, отраженной от объекта или излученной с него, не совпадает с истинным направлением на объект. Угол прихода волны зависит от состояния тропосферы и ионосферы, он подвержен регулярным и случайным изменениям. Для точного определения угловых координат космических объектов радиотехническими методами необходимо вносить поправки на рефракционные ошибки, которые определяются теоретическим путем. При этом с достаточной степенью точности можно считать, что ошибки, вызванные рефракцией в тропосфере и ионосфере, суммируются.

Рассмотрим сначала, как определяется рефракционная ошибка в тропосфере. Рефракционной ошибкой называется угол между истинным направлением на космический объект и касательной к траектории волны в точке расположения приемной антенны (направления АС и АВ на рис. 8.4).

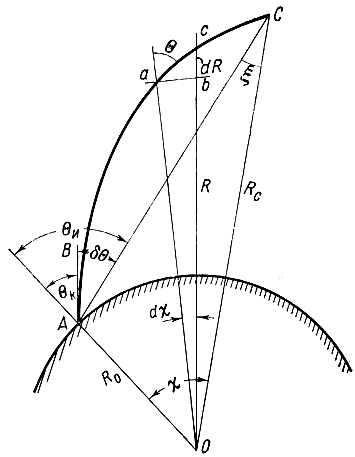
Рис. 8.4. К вычислению рефракционной ошибки тропосферы

Из рис. 8.4 следует, что рефракционная ошибка δθ определяется как разность углов θ_и и θ_к:

Угол θ_и как внешний угол треугольника АОС равен сумме углов χ и ξ:

а

где R_c - расстояние от центра земного шара до объекта. Из выражений (8.4), (8.5) и (8.6) следует, что

Элементарный центральный угол при дуге ab - dχ определяется соотношением

где R - текущее расстояние от центра земного шара до траектории волны.

Из элементарного треугольника abc получаем выражение для дуги аb:

где θ - текущий угол между направлением радиуса земного шара и касательной к траектории волны.

Из уравнения траектории волны в сферически неоднородной слоистой среде [см. уравнение (3.19)]:

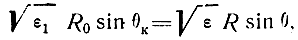
где ε₁ - относительная диэлектрическая проницаемость тропосферы вблизи поверхности Земли, определяют tgθ:

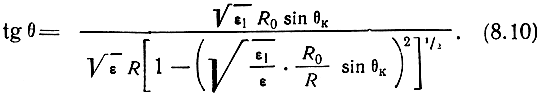
Подставляя выражение (8.10) в (8.9), а затем в (8.8) и интегрируя величину dχ получаем значение угла χ:

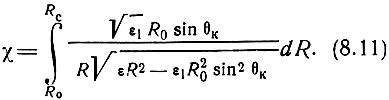
Подстановка формулы (8.11) в (8.7) дает окончательное выражение для рефракционной ошибки:

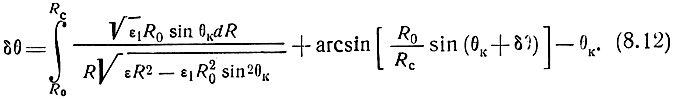
Величину δθ вычисляют, задаваясь определенным законом изменения ε с высотой. Результаты вычислений рефракционной ошибки, вносимой нормальной тропосферой, в зависимости от угла возвышения спутника при высоте 450 км показаны на рис. 8.5 (пунктирная линия) [38, 57].

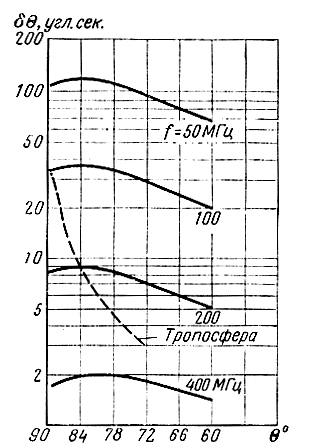
Рис. 8.5. Сопоставление рефракционных ошибок, вызванных тропосферой и ионосферой на волнах частотой 50, 100, 200 и 400 МГц, в зависимости от угла возвышения спутника: ^___ ионосфера; --- тропосфера

Из рисунка видно, что рефракционная ошибка резко убывает с увеличением угла возвышения. Кроме того, расчеты показывают, что рефракционная ошибка возрастает с увеличением влажности воздуха.

Рефракционная ошибка, вызванная влиянием ионосферы, может быть вычислена по формуле, аналогичной (8.12). Разница заключается в том, что в соответствии с рис. 8.6 уравнение траектории волны запишется как

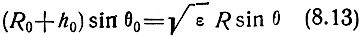
и выражение (8.10) примет несколько иной вид:

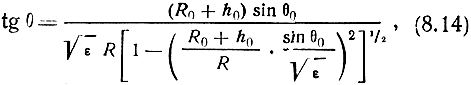
благодаря чему в формулу (8.12) войдет зависимость рефракционной ошибки от высоты ионосферы.

Так как относительная диэлектрическая проницаемость ионосферы зависит от рабочей частоты, то и рефракционная ошибка, вызываемая ионосферой, имеет частотную зависимость. В первом приближении δθ изменяется обратно пропорционально квадрату частоты.

На рис. 8.5 показана зависимость рефракционной ошибки, вызванной ионосферой, от угла возвышения спутника при высоте 450 км (сплошные линии). При расчетах взята максимальная электронная плотность ионосферы [38, 57].

Рефракционные ошибки, вызванные влиянием тропосферы и ионосферы, соизмеримы при рабочей частоте около 200 МГц. На частотах 50÷100 МГц тропосферную рефракцию можно не учитывать. На частотах выше 400 МГц рефракционные ошибки, вносимые ионосферой, ничтожно малы. Тропосфера и ионосфера являются статистически неоднородными средами. Флуктуации коэффициентов преломления этих сред обусловливают флуктуации угла прихода радиоволн, и поправка на зенитный угол, помимо среднего значения, имеет нерегулярную составляющую.