Раздел первый. Электронные приборы сверхвысоких частот

Глава первая. Основы работы электронных приборов диапазона сверхвысоких частот

1-1. Особенности электронных приборов СВЧ

Электронные приборы сверхвысоких частот отличаются от электронных ламп рядом особенностей. Несмотря на то что в диапазоне сверхвысоких частот используются приборы различных типов, основные особенности остаются общими для всех приборов, нашедших широкое техническое применение. Поэтому перед изучением конкретных электронных приборов СВЧ диапазона ознакомимся с некоторыми из этих особенностей.

Использование обычных электронных ламп (диодов, триодов, пентодов и др.) в диапазоне дециметровых и сантиметровых волн ограничивается главным образом инерцией электронов и влиянием распределенных реактивностей: междуэлектродных емкостей и индуктивностей вводов. Основные особенности электронных приборов СВЧ диапазона связаны с устранением влияния перечисленных факторов.

Первая особенность этих электронных приборов заключается в том, что сам прибор составляет единое целое с колебательной системой. Поэтому изучение принципа действия электронных приборов СВЧ, их параметров и характеристик невозможно в отрыве от колебательных систем, которые отличаются от резонансных систем, используемых в диапазоне длинных и средних волн.

Вторая особенность электронных приборов СВЧ состоит ив том, что время пролета электронов от катода к электроду, собирающему отработанные электроны, используется для формирования электронного потока (образования сгустков и разрежений в потоке движущихся электронов), а также для передачи энергии от электронов высокочастотному электрическому полю. Иначе говоря, принцип работы приборов СВЧ основан на полезном использовании времени движения электронов, которое может быть равно единицам и даже десяткам периодов рабочей частоты.

1-2. Принцип действия электронных приборов СВЧ

Электронные приборы СВЧ диапазона, как и приборы других типов, служат преобразователями одного вида энергии в другой.

Как известно, в усилителях или генераторах, использующих обычные электронные лампы, увеличение мощности усиливаемых колебаний или восполнение потерь в колебательных системах автогенератора происходит за счет энергии источника постоянного напряжения, питающего электроды лампы. Электронный поток является своеобразным "посредником" при таком преобразовании энергии. СВЧ приборы в этом смысле ничем не отличаются от обычных электронных ламп: здесь также энергия источника постоянного напряжения преобразуется в энергию СВЧ колебаний.

Отличие СВЧ приборов, помимо особенностей колебательных систем и методов их сопряжения с прибором, заключается в управлении электронным потоком в приборе. Если в обычных электронных лампах управление электронным потоком статическое, где с изменением переменного напряжения на сетке меняется плотность электронного потока, то в СВЧ приборах электронный прибор управляется динамически. Электрическое поле, образуемое сверхвысокочастотными колебаниями, используется здесь для изменения скорости электронного потока, а не его плотности. И лишь со временем, в процессе дальнейшего движения электронов, в результате разности их скоростей в электронном потоке образуются сгущения и разрежения.

Создание электронного потока, плотность которого является функцией времени, необходимо для эффективной передачи энергии движущихся электронов сверхвысокочастотному электромагнитному полю. При взаимодействии с этим полем электроны могут отдавать ему как кинетическую, так и потенциальную энергию.

Рассмотрим один из возможных случаев, когда высокочастотному полю передается кинетическая энергия. Предположим (рис. 1-1, а), что электроны, эмиттированные катодом и ускоренные полем ускоряющего электрода, находящегося под положительным потенциалом U, движутся далее равномерным потоком. На их пути расположены обкладки конденсатора С, образующего с индуктивностью L колебательный контур, в котором возбуждены колебания с частотой ω. Обкладки конденсатора выполнены в виде сеток, так что электроны свободно проходят через обе обкладки. В то же время ввиду высокой частоты колебаний сетки служат экранами и сверхвысокочастотное электрическое поле сосредоточено в зазоре между сетками. Осевая составляющая вектора ε напряженности этого поля в течение одной половины периода совпадает по направлению с вектором υ_e скорости электронов, а во время другой половины периода - противоположна ему. Если плотность электронного потока постоянна во времени, то за первую половину периода поле ε тормозит столько же электронов, сколько ускоряет их за вторую половину периода. Иначе говоря, электрическое поле в течение периода колебаний приобретает и теряет равные порции энергии и, следовательно, передачи энергии от электронов полю не будет.

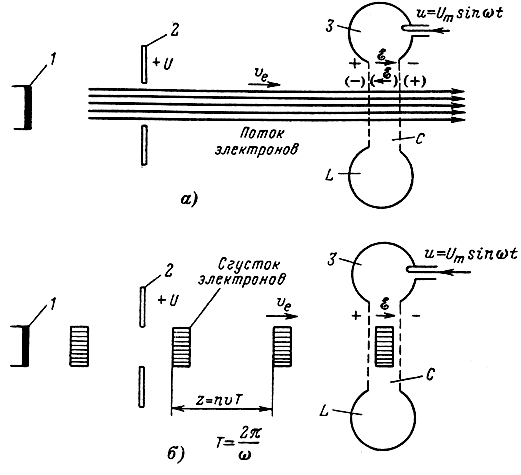
Рис. 1-1. Обмен энергией между электронным потоком и электрическим полем резонатора. а - при непрерывном потоке; б - при сгруппированном потоке электронов; 1 - катод; 2 - ускоряющий электрод; 3 - колебательный контур

Для того чтобы энергетический баланс был положительным, т. е. чтобы энергия электрического поля пополнялась, необходимо получить прерывистый поток электронов (рис. 1-1, б). В этом случае временные интервалы между отдельными группами электронов и время прихода первого из них к щели резонатора можно выбрать такими, чтобы электроны попадали в электрическое поле резонатора только в те моменты времени, когда поле для них тормозящее. Для выполнения этого необходимо, чтобы сгустки электронов отставали друг от друга на время, равное периоду колебаний Т или целому числу периодов.

Если время пролета сгустков электронов между сетками резонатора меньше Т/2, а в интервалах между сгустками плотность электронного потока равна нулю, то энергия будет передаваться только в одном направлении: от электронов - полю.

В реальных условиях осуществить такую идеальную модуляцию электронного потока по плотности невозможно и в интервалах между сгустками плотность потока, хотя и значительно меньше чем в сгустках, но все же не равна нулю. В этом случае поле затрачивает некоторую энергию на ускорение электронов, находящихся между сгустками. Но так как их плотность сравнительно невелика, то общий баланс энергии в среднем за период остается положительным.

В СВЧ электронных приборах сгруппированный в сгустки электронный поток получается при модуляции непрерывного потока электронов по скорости. В качестве модулирующего напряжения используются СВЧ колебания, подлежащие усилению (в усилителях), или же часть энергии (в автогенераторе), отводимая в модулирующее устройство через цепь обратной связи.

В рассмотренном только что случае электроны взаимодействуют с пульсирующим полем, сосредоточенным в определенной части пространства - между сетками резонатора. Такое пульсирующее поле может быть использовано и для модуляции электронного потока по скорости, в результате которой образуются сгустки электронов.

Существует, однако, обширная группа сверхвысокочастотных приборов, в которых процессы модуляции электронного потока и последующего взаимодействия электронных сгустков с полем протекают в процессе совместного движения электронов и бегущей - движущейся в пространстве электромагнитной волны. Происходит не кратковременное (на определенном отрезке пути), а длительное взаимодействие электронов с полем на всем пути их совместного движения. Такие приборы, обладающие определенными преимуществами, называют часто приборами длительного взаимодействия.

Характер взаимодействия электронов со сверхвысокочастотным полем не ограничивается описанным выше случаем передачи полю кинетической энергии. Во многих приборах электроны отдают полю потенциальную энергию, перемещаясь по сложным траекториям во взаимно перпендикулярных электрическом и магнитном полях.

Электронные приборы, в которых электроны движутся в продольных электрическом и магнитном полях, называют приборами типа О. Приборы же, в которых используются скрещенные электрические и магнитные поля, с векторами, перпендикулярными вектору скорости электронов, называют приборами типа М.

Для всех электронных приборов диапазона СВЧ характерен, однако, процесс формирования прерывистого электронного потока, сгустки которого и обеспечивают эффективный энергетический обмен с электромагнитным СВЧ полем.

1-3. Колебательные системы приборов СВЧ

В этом параграфе мы кратко напомним об основных особенностях и характеристиках колебательных систем^*, используемых в электронных приборах диапазона сверхвысоких частот.

^* (Основы теории линий передач и колебательных систем последовательно изучаются в курсах "Основы теории цепей", "Радиотехнические цепи и сигналы", "Электродинамика" и др.; поэтому дальнейшее рассмотрение принципов работы и физических процессов в электронных СВЧ приборах базируется на материале этих курсов.)

Колебательные системы электронных СВЧ приборов можно условно разделить на две группы: узкополосные резонаторы и широкополосные, обычно называемые замедляющими системами.

Узкополосные колебательные системы. К этой группе относятся замкнутые вибраторы (эндовибраторы) различных форм, резонаторы типа щель - отверстие, а также короткозамкнутые отрезки коаксиальных линий и волноводов. Развитие и широкое применение колебательных систем этих видов связано с началом освоения радиотехникой в 30-х годах дециметрового и сантиметрового диапазонов радиоволн.

Наиболее широкое применение в электронике СВЧ нашли колебательные системы, в которых электрическое и магнитное поля как бы отделены в пространстве друг от друга (рис. 1-2, б-д). В этих колебательных системах части плоскостей, расположенные на небольшом расстоянии друг от друга, образуют емкость, в которой сосредоточено электрическое поле. В остальной части объема, эквивалентной индуктивности контура, сосредоточено в основном магнитное поле. Примерные картины электрических и магнитных полей в таких резонаторах показаны на рис. 1-3. Концентрация высокочастотного электрического поля в небольшой части пространства имеет весьма важное значение, так как передача энергии от электронного потока в колебательную систему происходит во многих приборах в результате взаимодействия движущихся электронов с переменным электрическим полем.

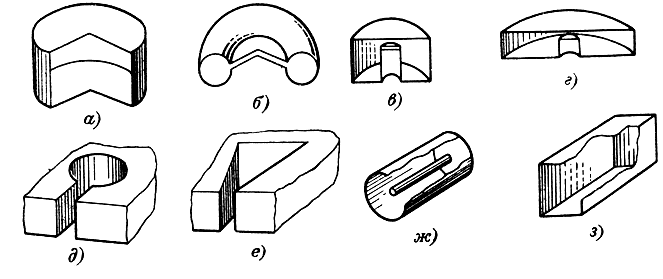
Рис. 1-2. Узкополосные колебательные системы СВЧ диапазона. а - цилиндрический резонатор; б - тороидальный резонатор; в - отрезок коаксиальной линии с емкостью в торце; г - отрезок радиальной линии с емкостью в середине; д - резонатор щель - отверстие; е - трапециевидный резонатор; ж - короткозамкнутый отрезок коаксиальной линии; з - короткозамкнутый отрезок волновода

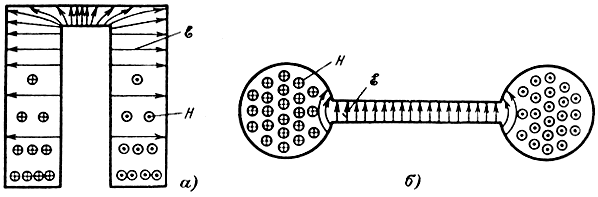
Рис. 1-3. Электрическое и магнитное поля. а - в резонаторе, образованном отрезком коаксиальной линии с емкостью в торце; б - в тороидальном резонаторе

Колебательные контуры, составленные из сосредоточенных элементов L и С, характеризуются емкостью, индуктивностью, связанной с этими величинами резонансной частотой

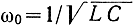
и добротностью. В колебательных системах СВЧ диапазона невозможно полностью разграничить индуктивность и емкость. Для коаксиальных или волноводных линий передачи иногда пользуются понятиями погонной индуктивности и погонной емкости, т. е. величинами L и С, приходящимися на единицу длины. Колебательные системы СВЧ диапазона обычно характеризуют тремя величинами: резонансной частотой при основном виде колебаний, добротностью и эквивалентной проводимостью.

В замкнутых колебательных системах может возникнуть множество различных колебаний, отличающихся частотой и соответственно распределением электрического и магнитного полей внутри объема резонатора. Но, как правило, наибольшей интенсивностью характеризуется один из простейших видов колебаний, для которого граничные условия удовлетворяются наилучшим образом. Так, например, для резонатора, образованного отрезком коаксиальной линии с емкостью в торцевой части (рис. 1-2, в), основным видом колебаний будет такой, когда вдоль линии укладывается четверть волны. Распределение электрического и магнитного полей на рис. 1-3, а показано именно для этого случая.

Добротность замкнутых колебательных систем весьма высока (порядка сотен и тысяч единиц), так как электромагнитное поле заключено внутри оболочки, образующей резонатор. Сама оболочка, металлическая или металлизированная внутри, служит экраном, и потери на излучение практически отсутствуют. Потери в самом резонаторе невелики, так как форму резонатора стараются сделать такой, чтобы в местах пучности тока периметр поверхности, обтекаемой этим током, был как можно меньше. Кроме того, внутреннюю поверхность покрывают обычно тонким слоем металла с малым удельным сопротивлением (серебро или золото) и затем полируют для уменьшения микроскопических неровностей и сокращения пути тока. Потери в самом резонаторе часто характеризуют эквивалентной проводимостью потерь

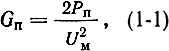
где Р_п - мощность, теряемая в резонаторе; U_M - амплитуда высокочастотного напряжения.

Если резонатор нагружен, т. е. часть электромагнитной энергии отводится из резонатора в нагрузку, то пользуются понятием проводимости нагруженного резонатора

где G_н - активная проводимость самой нагрузки.

Резонатор связывается с нагрузкой витком связи или емкостным штырем (рис. 1-4). В первом случае преобладает индуктивная связь. В витке, плоскость которого располагают перпендикулярно силовым линиям магнитного поля, индуцируется э. д. с. Виток связи помещают в пучность тока. Регулировка степени связи производится поворотом витка относительно его оси. Во втором случае связь - емкостная. Штырь вводят в пучность напряжения и регулируют связь, изменяя зазор между штырем и стенкой резонатора.

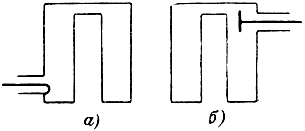
Рис. 1-4. Устройство связи линии с резонатором. а - индуктивная связь с помощью витка; б - емкостная связь с помощью штыря

Замедляющие системы. В качестве широкополосных колебательных систем в СВЧ приборах применяются замедляющие системы, некоторые типы которых в качестве примера показаны на рис. 1-5. Чаще всего одна из линий замедляющей структуры имеет гладкую поверхность, а другая - характеризуется рядом периодически повторяющихся ячеек. Иногда (рис. 1-5, г) обе линии имеют периодическую структуру. Гладкую линию называют обычно основанием или холодным катодом.

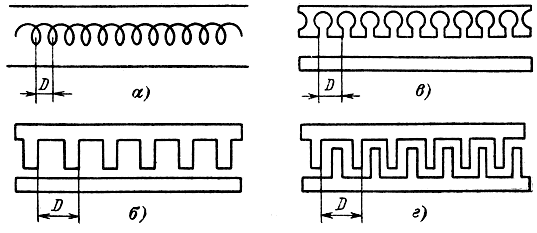
Рис. 1-5. Замедляющие системы. а - коаксиальная линия со спиральным внутренним проводником; б - гребенчатая; в - цепочка резонаторов щель - отверстие; г - две гребенки

Расстояние между соседними идентичными элементами замедляющей системы называется периодом структуры (величина D на рис. 1-5).

Если величина D периода структуры соизмерима с длиной волны в колебаний, распространяющихся по замедляющей системе, то такая система неоднородна. В случае же D ≤ λ_в замедляющую систему называют квазиоднородной или просто однородной.

Замедление. Основное назначение замедляющей системы - уменьшить скорость распространения электромагнитной волны. Как мы увидим далее, эффективное взаимодействие потока электронов с полем волны может быть получено только при условии приблизительного равенства фазовой скорости волны υ_ф и скорости υ_e движения электронов. При реально допустимых ускоряющих напряжениях, порядка сотен или тысяч вольт, скорость υ_e движения электронов не превышает сотых или десятых долей от величины с -скорости света. Таким образом, фазовая скорость υ_ф волны должна быть в несколько единиц или десятков раз меньше скорости с. Отношение с/υ_ф называют коэффициентом замедления системы. В реальных приборах c/υ_ф (3 ÷ 50).

Анализ решения волнового уравнения для передающих линий с гладкими стенками показывает невозможность получения замедленных волн в таких структурах, так как на поверхности линии не выполняются требуемые граничные условия.

Замедление волны может быть достигнуто лишь в таких линиях передачи, поверхностное сопротивление которых имеет реактивный характер. Показанные на рис. 1-5 замедляющие системы удовлетворяют этому требованию.

Принцип замедления волны легко показать на примере спиральной замедляющей системы (рис. 1-5, а), представляющей собой коаксиальную линию передачи со спиральным внутренним проводником. При возбуждении такой линии от генератора СВЧ колебаний волна распространяется по внутреннему проводнику со скоростью, близкой к скорости света. Следовательно, за время движения вдоль одного витка спирали длиной 2 πr, где r - радиус спирали, волна переместится вдоль оси системы лишь на величину D - шага спирали. Таким образом, коэффициент замедления

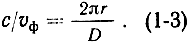
Полезно рассмотреть принцип замедления волны и с несколько иной точки зрения. Предположим, что генератор СВЧ колебаний с частотой ω питает линию, подобную изображенной на рис. 1-5, в. Такую линию, впрочем, как и любую другую замедляющую систему, но более наглядно, можно представить как цепочку элементарных резонаторов, емкость С₀ которых образуется щелью, а индуктивность L₀ - отверстием.

При распространении волны на поверхности линии наводятся токи, которые, протекая по резонаторам, возбуждают в них колебания с частотой ω. Амплитуда и фаза вынужденных колебаний зависят от соотношения частот ω/ω₀, где

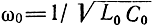
- собственная резонансная частота резонатора. Эти зависимости иллюстрируются амплитудной и фазовой характеристиками элементарного резонатора (рис. 1-6). Фазовый сдвиг вынужденных колебаний в зависимости от со изменяется от -π/2 до +π/2. Вынужденные колебания резонаторов накладываются на возбуждающие, и фаза результирующей волны изменяется. Появляется сдвиг фазы между результирующей и возбуждающей волнами. По мере движения волны вдоль линии этот фазовый сдвиг накапливается, так как волна подвергается воздействию вынужденных колебаний в следующих резонаторах. Увеличивающееся по мере движения отставание по фазе результирующей волны от возбуждающей означает, что фазовая скорость первой из них меньше фазовой скорости последней.

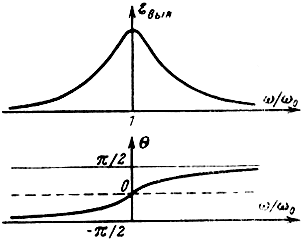
Рис. 1-6. Резонансная кривая и фазовая характеристика колебательного контура

Электрическое поле в замедляющей системе. Итак, при распространении электромагнитной волны по замедляющей структуре фаза колебаний в соседних резонаторах отличается на некоторую величину φ

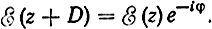
Картина электрического поля на отрезке замедляющей системы для некоторого момента времени t показана на рис. 1-7, а. Электрическое поле сосредоточено вблизи щелей резонаторов. Поэтому зависимость продольной составляющей поля

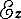
от координаты z (рис. 1-7, б) представляет собой серию импульсов с синусоидальной огибающей. Через некоторый интервал времени Δt волна переместится на величину Δz и максимальная величина продольной составляющей поля окажется вблизи одного из следующих резонаторов (пунктирная огибающая). По истечении половины периода фаза колебаний в каждом из резонаторов изменится на противоположную. Таким образом, величина поля εz вблизи каждого резонатора будет меняться в такт с частотой со колебаний генератора, питающего линию, проходя все значения от наибольшего положительного (вектор εz совпадает по направлению с осью z) до наиболее отрицательного.

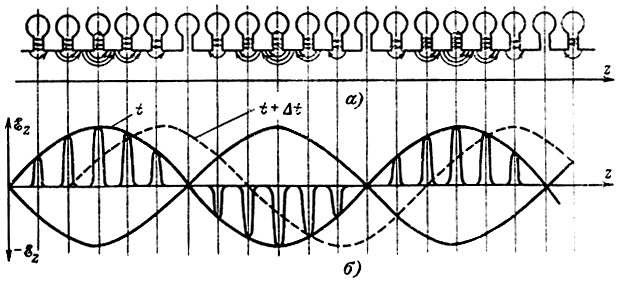
Рис. 1-7. Картина электрического поля у поверхности замедляющей системы (а) и зависимость (б) продольной составляющей поля εz от координаты z

В любой момент времени, однако, функция εz(z) представляет собой как бы последовательность импульсов с периодом следования, равным периоду структуры D. Такая функция может быть, подобно временной последовательности импульсов, представлена комплексным рядом Фурье

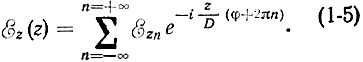
Пространственные гармоники. Иначе говоря, поле вдоль замедляющей системы можно представить как результат наложения бесконечного числа бегущих волн, подобно тому как несинусоидальное во времени колебание представляется в виде бесчисленного множества гармонических составляющих. Только при гармоническом анализе функции ε(t) получаются компоненты с различными - кратными основной - частотами, а при разложении в ряд Фурье функции ε(z) - группа пространственных гармоник, для которых набег фазы на пути D отличается на 2πn радиан, где n - целое число, включая нуль.

Показатель степени е

в выражении (1-5) определяет набег фазы любой из пространственных гармоник на отрезке z, так как изменение фазы на длине D равно φ + 2πn.

Следовательно, пространственные гармоники отличаются фазовой скоростью

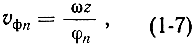
коэффициентом фазы

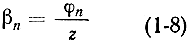
и длиной волны в линии

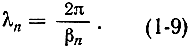
Частота колебаний для всех пространственных гармоник одна и та же - частота ω генератора, питающего линию.

Необходимо подчеркнуть, что граничные условия в неоднородной замедляющей системе не выполняются ни для одной пространственной гармоники в отдельности и, следовательно, ни одна из них не может существовать изолированно от других. Граничным условиям удовлетворяет лишь совокупность бесконечно большого числа пространственных волн с различной фазовой скоростью.

Амплитуда результирующей волны в любой точке линии есть результат суперпозиции в этой точке всех пространственных волн, фазы которых различны.

Движение результирующей волны вдоль линии, т. е. перемещение некоторой точки огибающей, полученной в результате суммирования пространственных волн, характеризуется групповой скоростью, определяемой соотношением

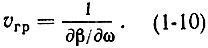
Используя (1-7), запишем (1-8) в виде

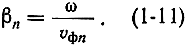
Дифференцируя это выражение по со и подставляя в (1-10), получим известную формулу Рэлея, связывающую групповую скорость с фазовой:

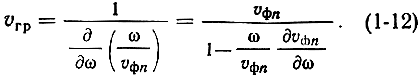
Найдем теперь выражение, определяющее фазовые скорости пространственных гармоник, для чего подставим (1-6) в (1-7):

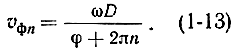
Вообще говоря, знак при п может быть любым: n = 0; ±1; ±2; ±3 ..., так как прибавление к фазе φ или вычитание из этой величины целого числа 2π не изменит фазы поля. Но при положительных n фазовая скорость гармоник согласно (1-13) оказывается положительной, а при отрицательных n она отрицательна.

В первом случае пространственные гармоники называются прямыми, а во втором случае - обратными.

Знак "плюс" перед величиной υ_фn означает, что векторы фазовых скоростей прямых гармоник совпадают по направлению с век-втором групповой скорости. Для обратных гармоник фазовые скорости по направлению противоположны вектору υ_гр.

Гармоника, соответствующая n = 0, называется нулевой. В электронных приборах обычно используется взаимодействие электронов с гармониками, соответствующими n = 0; ±1.

Рассмотрим физический смысл положительной и отрицательной фазовой скорости, не забывая о том, что групповая скорость волны направлена от генератора к нагрузке.

Изменение фазы пространственной гармоники на пути D можно представить как поворот радиус-вектора ε на угол φ (рис. 1-8). Для небольших φ последовательные положения радиус-вектора при движении волны от генератора к нагрузке (вращение против часовой стрелки) отмечены цифрами 1, 2, 3... Если же φ велико, например лишь несколько меньше 2π, то последовательные положения радиус-вектора будут иными (1', 2', 3' и т. д.).

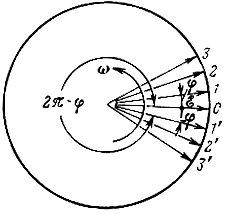
Рис. 1-8. Вращение радиус-вектора ε, иллюстрирующее понятия положительной и отрицательной фазовых скоростей

Во втором случае можно говорить о последовательных поворотах радиус-вектора на угол - φ, т. е. об отрицательном набеге фазы при движении волны вдоль линии. Кажущееся направление вращение вектора противоположно действительному: фазовая скорость отрицательна, хотя направление движения волны (групповая скорость) осталось прежним.

Подобный эффект можно наблюдать в кино при движении экипажа на колесах, снабженных спицами. При некоторой скорости движения угол поворота колеса отличается от угла ψ, образованного соседними спицами, на небольшую величину: Δψ ≤ ψ. При последовательном проектировании кадров отставание спиц от положения, соответствующего предыдущему кадру, накапливается и создается эффект вращения колеса в обратном направлении.

Дисперсия - зависимость фазовой скорости от частоты - одно из важнейших свойств замедляющих систем. Выше уже отмечалось, что вынужденные колебания в резонаторах отличаются по фазе от возбуждающей волны. Как видно из рис. 1-6, величина этого фазового сдвига в зависимости от соотношения ω/ω₀ может изменяться в пределах от -π/2 до +π/2. Вдали от резонанса при ω ≤ ω₀ амплитуда вынужденных колебаний мала и поэтому вектор

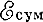
суммарной волны мало отличается по фазе от вектора

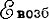
волны возбуждающей (рис. 1-9, а).

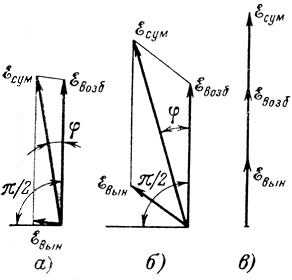
Рис. 1-9. Сложение векторов возбуждающего и вынужденного колебаний. а - вдали от - резонанса; б - вблизи резонанса; в - при резонансе

Фазовый сдвиг, добавляющийся вблизи щели каждого следующего резонатора, невелик, и фазовая скорость мало отличается от скорости с распространения волны в свободном пространстве (рис. 1-10). По мере приближения к резонансу амплитуда вынужденных колебаний увеличивается, но при этом уменьшается их фазовый сдвиг относительно возбуждающей волны (см. рис. 1-6). Вначале при ω < ω₁ амплитуда растет быстрее, чем уменьшается сдвиг фаз. Растет поэтому и влияние вынужденных колебаний на результирующую волну. Отставание результирующей волны по фазе от возбуждающей увеличивается (рис. 1-9, б) и υ_ф уменьшается. Далее, при ω₁ < ω < ω₀ рост амплитуды замедляется, а фазовый сдвиг быстро уменьшается до нуля при ω = ω₀. Поэтому и сдвиг фаз между возбуждающей и результирующей волнами уменьшается до нуля при резонансе (рис. 1-9, в), а фазовая скорость результирующей волны растет и при ω = ω₀ становится равной скорости с.

Таким образом, в замедляющей системе на частотах ω < ω₀ фазовая скорость волны может быть значительно меньше скорости света.

При дальнейшем увеличении частоты (ω > ω₀) все сказанное можно повторить в обратном порядке с тем лишь отличием, что фазовый сдвиг между результирующей и возбуждающей волнами меняет знак на обратный. Поэтому далее с увеличением со фазовая скорость сначала растет и становится больше с, а затем уменьшается, приближаясь к этой величине при ω ≥ ω₀.

Из проведенного рассмотрения следует, что фазовая скорость распространения волны вдоль замедляющей системы зависит от частоты: линия обладает дисперсией.

Из рис. 1-10 видно, что при всех значениях ω, исключая узкую область (ω₂ - ω₁) вблизи ω₀, производная ∂υ_ф/∂ω < 0. Такая зависимость фазовой скорости от частоты называется нормальной дисперсией. И, наоборот, зависимость υ_ф = f(ω), при которой ∂υ_ф/∂ω > 0, называется аномальной дисперсией (область ω₂ - ω₁).

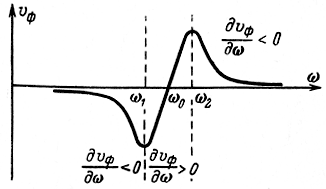
Рис. 1-10. Кривая зависимости υ_ф = f(ω)

Кривая на рис. 1-10, поясняющая физическую сущность дисперсии, неудобна для оценки дисперсионных свойств замедляющих систем. Чаще всего дисперсионные характеристики замедляющих систем, иллюстрирующие дисперсию пространственных гармоник, строятся в виде зависимостей c/υ_фn = f(λ) (рис. 1-11).

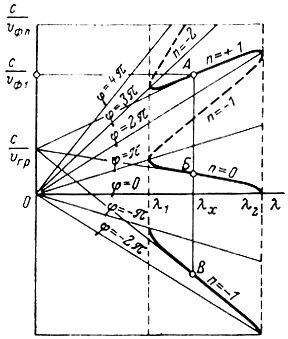
Рис. 1-11. Дисперсионные характеристики замедляющей системы с положительной дисперсией

Прямые, выходящие из начала координат, являются линиями разных фазовых сдвигов φ_n = const, построенными на основании соотношения

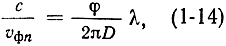
которое может быть легко получено из (1-7).

Вертикальными линиями отмечены границы полосы пропускания системы, соответствующие длинам волн λ₁ и λ₂, для которых φ₀,

например (при n = 0), принимают значение 0 и π, φ₁ (при n = +1) - значения 2π и 3π и т. д.

Таким образом, дисперсионная характеристика нулевой гармоники заключена между осью абсцисс и прямой φ = π; первой прямой гармоники - между прямыми φ = 2π и φ = 3π; первой обратной - между прямыми φ = -π и φ = -2π и т. д. Обычно дисперсионные кривые обратных гармоник переносят в верхнюю полуплоскость чертежа, как это показано пунктиром для 1-й и 2-й обратных гармоник.

По этим характеристикам, зная длину волны λ в свободном пространстве, легко определить коэффициент замедления и фазовую скорость любой гармоники, проектируя соответствующую точку (например, точку А для длины волны λ_х) на ось ординат.

Касательная к дисперсионной характеристике в заданной точке отсечет на оси ординат отрезок, равный c/υ_гр. Легко убедиться, что при заданной длине волны λ_х групповые скорости всех гармоник одинаковы (касательные к точкам А, Б и В) и равны групповой скорости волны.

Виды дисперсии. Выше уже отмечалось, что при ∂υ_ф/∂ω < 0 дисперсию называют нормальной, а при ∂υ_ф/∂ω > 0 - аномальной. Применительно к зависимости υ_ф = f(λ) нормальной дисперсии соответствует положительный знак производной (∂υ_ф/∂λ > 0), а аномальной - отрицательный знак (∂υ_ф/∂λ < 0).

Помимо этого различают также положительную и отрицательную дисперсии в зависимости от знака при υ_ф. Для прямых гармоник (υ_ф > 0) дисперсия положительна, а для обратных (υ_ф < 0) - отрицательна.

Обычно в электронных приборах используются замедляющие системы с положительной нормальной дисперсией (в лампах бегущей волны) или с отрицательной нормальной дисперсией (в лампах обратной волны).

Электрическое поле пространственных гармоник. Практически во всех электронных СВЧ приборах важную роль во взаимодействии электронов с волной играет продольная составляющая электрического поля той пространственной гармоники, для которой обеспечивается условие синхронизма (υ_е ≈ υ_фn).

Вычисление амплитуд пространственных гармоник - членов ряда Фурье (1-5) показывает, что с увеличением n не только уменьшается амплитуда поля непосредственно у поверхности замедляющей системы, но и растет степень уменьшения εz по мере удаления от поверхности (рис. 1-12).

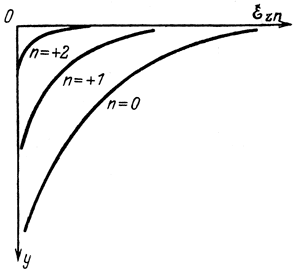
Рис. 1-12. Затухание амплитуд гармоник при удалении от поверхности замедляющей системы

Таким образом, при использовании пространственных гармоник с n > 1 пришлось бы формировать электронный поток так, чтобы он двигался на очень малом расстоянии от поверхности системы. Это вызывает серьезные конструктивные трудности и, кроме того, как мы увидим далее, существенно уменьшает эффективность передачи энергии от электронов полю в приборах типа М.

Сопротивление связи. В электронных СВЧ приборах обычно измеряют мощность электромагнитной волны. Поэтому очень важно знать связь между напряженностью электрического поля и мощностью волны. С этой целью вводят специальный параметр - сопротивление связи R_c, характеризующий соотношение между амплитудой

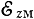
напряженности электрического поля и потоком мощности Р, проходящим через поперечное сечение замедляющей системы:

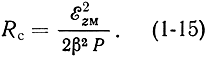
Каждая пространственная гармоника характеризуется своим сопротивлением связи

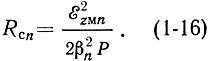
В реальных приборах величина сопротивления связи лежит в пределах от нескольких десятков до нескольких сотен ом.

Как будет показано далее, при рассмотрении конкретных приборов с помощью сопротивления связи определяются такие важные параметры приборов, как коэффициент усиления, рабочий диапазон частот, к. п. д. и др.