
Глава вторая. Клистроны
2-1. Двухрезонаторный усилительный клистрон. Принцип действия
Определение. Клистронами называют сверхвысокочастотные электронные приборы, использующие принцип скоростной модуляции электронного потока и содержащие один или несколько объемных резонаторов. Клистроны применяются для усиления, генерирования и умножения частоты СВЧ колебаний. Их колебательные системы узкополосные, и перестройка клистронных усилителей или генераторов в широком диапазоне волн производится, как правило, механически, изменением геометрических размеров резонаторов.
Устройство. Схематически устройство двухрезонаторного усилительного клистрона показано на рис. 2-1. Электроны, испускаемые подогревным катодом, увлекаются полем ускоряющего электрода, на который подается положительное напряжение U0. Этот электрод также несколько фокусирует электронный поток, движущийся далее к первому объемному резонатору. Часть резонатора выполнена в виде сеток, находящихся внутри баллона прибора и образующих емкость колебательного контура. К этому резонатору, называемому обычно модулятором, через коаксиальную линию или волновод и петлю связи подводятся СВЧ колебания, подлежащие усилению. Второй аналогичный резонатор называется улавливателем. Петлей связи усиленные колебания отводятся из улавливателя в нагрузку. Электронный поток движется от катода мимо ускоряющего электрода, сеток первого и второго резонаторов к коллектору, на который подано высокое положительное напряжение. Настройку резонаторов на частоту усиливаемых колебаний производят либо с помощью гибких стенок, при прогибе которых внешними винтами изменяется объем резонатора, либо специальными плунжерами, вводимыми внутрь резонатора и меняющими его индуктивность или емкость.
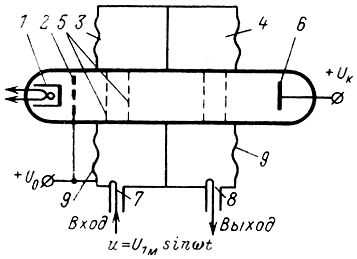
Рис. 2-1. Устройство двухрезонаторного клистрона. 1 - катод; 2 - ускоряющий электрод; 3 - входной резонатор; 4 - выходной резонатор; 5 - сетки резонатора; 6 - коллектор; 7 - петля связи на входе; 8 - петля связи на выходе; 9 - гибкие стенки
Принцип действия. Подводимый к модулятору сигнал u = U1мsinωt возбуждает в нем колебания с частотой ω, на которую настраивают оба резонатора. Переменное электрическое поле сосредоточено в емкости колебательной системы, образованной двумя сетками. Разность потенциалов между сетками модулятора меняется от нуля, когда емкость резонатора полностью разряжена и сетки находятся под одинаковым постоянным потенциалом U0, до величины U1м, когда вся колебательная энергия сосредоточена в емкости резонатора. Сетки резонатора служат хорошим экраном для электрического поля, меняющегося с высокой частотой. Поэтому разность потенциалов при перезаряде емкости резонатора меняется лишь в зазоре резонатора между его сетками. Поле же между ускоряющим электродом и первой сеткой резонатора, а также между двумя резонаторами остается неизменным. В этих междуэлектродных промежутках разность потенциалов всегда равна нулю, так как и ускоряющий электрод и оба резонатора находятся под одним и тем же потенциалом U0.
Электроны, движущиеся от ускоряющего электрода непрерывным потоком со скоростью
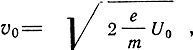
пролетая зазор модулятора, изменяют скорость в зависимости от мгновенной разности потенциалов между сетками. Закон изменения переменного напряжения на сетках и график движения электронов в промежутке между резонаторами - пространстве дрейфа показаны на пространственно - временной диаграмме (рис. 2-2).
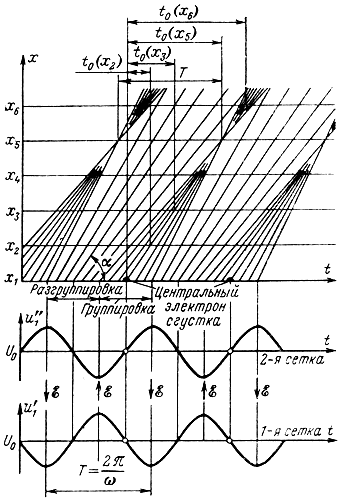
Рис. 2-2. Пространственно-временная диаграмма группирования электронов в двухрезонаторном клистроне
В нижней части диаграммы изображены кривые изменения сверхвысокочастотного напряжения на сетках первого резонатора.
Электроны, попадающие в зазор резонатора в течение той половины периода, когда переменное напряжение на второй сетке положительно и вектор напряженности ε переменного поля направлен навстречу движению электронов, ускоряются при пролете между сетками модулятора. В течение второй половины периода переменное напряжение на второй сетке отрицательно, вектор ε направлен от первой сетки ко второй и электроны, пролетая зазор, теряют свою скорость. Изменение скорости электронов определяется мгновенной разностью потенциалов и имеет наибольшие значения в моменты экстремумов переменного напряжения на сетках.
Для упрощения начального рассмотрения будем считать, что электроны скачкообразно изменяют свою скорость в середине зазора.
Верхняя часть диаграммы иллюстрирует движение электронов в пространстве дрейфа после их пролета через сетки резонатора. Ось времени проведена через точку х1 оси ординат, соответствующую середине зазора модулятора. График движения электронов в пространстве за резонатором представлен прямыми линиями, тангенс угла наклона которых к оси абсцисс пропорционален скорости движения электронов. Электроны, пролетевшие сетки резонатора в моменты прохождения переменного напряжения через нуль, движутся со средней скоростью υ0, и графики их движения наклонены к оси абсцисс под углом α, тангенс которого определяет скорость движения невозмущенного электрона.
Графики движения ускоренных электронов, прошедших резонатор, когда на второй сетке наступает положительный полупериод, наклонены к оси абсцисс под большим углом. И, наоборот, графики для электронов, прошедших зазор резонатора во время существования тормозящего поля, составляют с осью абсцисс меньший угол. Графики перемещения электронов, прошедших сетки резонатора в течение той половины периода, когда переменное напряжение на второй сетке изменяется от наиболее отрицательного до максимального положительного значения, пересекаются на некотором расстоянии x5 от середины зазора. Иначе говоря, на расстоянии х5 от середины резонатора происходит группирование этих электронов в сгусток. Другая часть электронов, прошедших резонатор в течение второй половины периода, разгруппировывается. Сгустки образуются вокруг электронов, движущихся со средней скоростью υ0 и минующих резонатор, когда напряжение на его второй сетке проходит через нуль, изменяясь от минимума к максимуму. В дальнейшем на расстояниях, превышающих х5, в результате сохраняющегося различия скоростей начинается разгруппирование электронов. Очевидно, что затем снова произойдет их группирование и т. д. Напряжение U0, амплитуда переменного напряжения U1м и расстояние между резонаторами подбираются таким образом, чтобы в момент образования сгустка электроны оказались в зазоре второго резонатора - улавливателя.
Сгустки электронов, разделенные одинаковыми промежутками времени, равными периоду усиливаемых колебаний, пролетают сетки второго резонатора и наводят в нем импульсы тока. Во втором резонаторе возникают СВЧ колебания с частотой, равной частоте колебаний, подводимых к модулятору. Фаза возбужденных колебаний такова, что в моменты прихода сгустков электронов поле между сетками второго резонатора оказывается тормозящим. Сгустки тормозятся в пространстве между сетками второго резонатора и передают свою энергию переменному электрическому полю, поддерживая таким образом возникшие в резонаторе колебания.
Мощность колебаний, установившихся во втором резонаторе, превышает мощность колебаний, подводимых к модулятору: происходит усиление СВЧ сигнала по мощности. Принцип усиления легко уяснить на основании энергетического рассмотрения описанных процессов. Энергия для разгона электронов, движущихся от катода через сетки резонаторов и далее к коллектору, получается от источника постоянного напряжения U0. Расход энергии источника усиливаемых колебаний на группирование электронов близок к нулю, так как в течение одной половины периода при ускорении электроны отбирают энергию от переменного электрического поля, а в течение другой - тормозятся и отдают свою энергию. Обмен энергией между электронным потоком и переменным электрическим полем во втором резонаторе происходит лишь в одном направлении: от электронов к полю, поскольку моменты существования ускоряющей разности потенциалов соответствуют интервалам между сгустками электронов. В моменты же прихода сгустков поле в зазоре второго резонатора всегда тормозящее. Таким образом, мощность колебаний увеличивается за счет отбора энергии от источника постоянного напряжения. Электронный поток служит лишь для передачи этой энергии переменному полю второго резонатора, а процесс модуляции электронов по скорости и группирования их в сгустки необходим для рациональной передачи этой энергии.
2-2. Группирование электронов в двухрезонаторном клистроне
Модуляция электронного потока по скорости. Электроны, входящие в зазор модулятора двухрезонаторного клистрона со скоростью
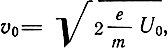
ускоряются или замедляются в соответствии с мгновенным значением переменного напряжения u = U1мsinωt. Поэтому для скорости электрона, прошедшего сетки модулятора, можно записать выражение
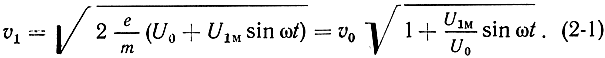
Обычно амплитуда переменного напряжения U1м значительно меньше постоянного напряжения U0 и корень в выражении (2-1) может быть представлен в виде первых двух членов ряда
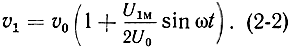
Коэффициент модуляции. До сих пор мы считали, что электроны, пролетая сетки модулятора, изменяют свою скорость скачком в середине зазора резонатора, и пренебрегали временем пролета электронов между сетками. В действительности же это время сравнимо с периодом колебаний и оказывает, как будет показано Далее, весьма существенное влияние на форму тока, наводимого сгустком электронов во втором резонаторе. Кроме того, конечное время пролета электронов между сетками модулятора влияет также и на сам процесс модуляции электронного потока.
Обозначим фазу напряжения между сетками резонатора в момент пролета электроном плоскости первой сетки через Θ1, а фазу Напряжения, соответствующую пролету электрона через вторую сетку - через Θ2. Тогда среднее значение переменного напряжения, воздействующего на электрон в течение времени его пролета между сетками модулятора, определится выражением
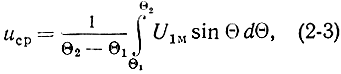
где Θ = ωt - фаза переменного напряжения в момент пролета электрона через середину резонатора.
Интегрируя, получим:
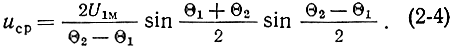
Полагая угол пролета электрона через зазор модулятора равным Θ3 и учитывая, что Θ3/2 = Θ - Θ1 = Θ2 - Θ, выражение (2-4) можно записать в виде
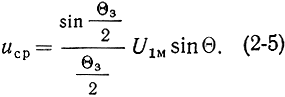
Величина
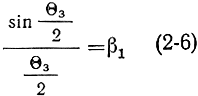
называется коэффициентом взаимодействия электронов с полем резонатора. Коэффициент β1 равен 1 при Θ3 = 0 и обращается в нуль, когда электрон находится в пространстве резонатора в течение всего периода переменного напряжения. В последнем случае модуляции электронного потока не произойдет и электроны после пролета сеток модулятора будут двигаться равномерным потоком.
Если электрон находится в зазоре модулятора в течение, например, положительного полупериода, то приращение его скорости пропорционально не
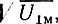
а корню из среднего значения напряжения за период
| uср | 2 | U1м | = 0,64 U1м | |
| π |
В клистронах угол пролета Θ3 лежит в пределах от π/2 до π. При этом коэффициент β1 ≈ 0,9 ÷ 0,6.
Учитывая влияние угла пролета Θ3 электронов в зазоре, выражение (2-2) следует записать в форме
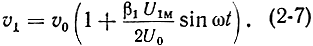
Величина
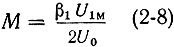
называется коэффициентом модуляции скорости электронного потока.
Параметр группирования. Вводя величину М в выражение (2-7), определяющее скорость электрона, получим:
υ1 = υ0(1 + M sinωt). (2-9)
Отсюда следует, что скорость электронов после пролета сеток резонатора состоит из постоянной величины υ0 и переменной составляющей, меняющейся во времени по закону синуса.
Из пространственно-временной диаграммы (рис. 2-2) видно, что это изменение скорости электронов приводит к модуляции электронного потока по плотности. На расстоянии х2 образуются незначительные уплотнения, которые затем увеличиваются, и на расстоянии х5 образуются плотные сгустки электронов. Чтобы найти закон изменения электронного тока во времени, определим угол пролета электрона до некоторой плоскости х, которой он достигает в момент времени tx. Время пролета электрона до этой плоскости равно:
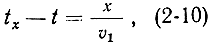
здесь t - время пролета электроном середины резонатора.
Подставляя сюда (2-9), получим:
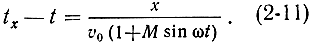
Учитывая, что М < 1, и обозначая t0 = x/υ0, запищем (2-11) в виде
tx - t = t0(1 - Мsinωt). (2-12)
Умножив обе части равенства на со и раскрыв скобки, получим выражение, связывающее угол пролета электронов в пространстве дрейфа с фазой переменного напряжения на сетках резонатора:
Θд = Θx - Θ = Θ0 - МΘ0 sinΘ, (2-13)
здесь Θд - угол пролета электронов от середины зазора модулятора до плоскости х; Θ0 - угол пролета этого же расстояния электроном, не изменившим своей скорости.
Величина, стоящая перед синусом в выражении (2-13), носит название параметра группирования:
МΘ0 = Х. (2-14)
Физический смысл этой величины мы обсудим несколько позже.
Закон изменения плотности тока. Используя (2-14), равенство (2-13) можно переписать в виде
Θд = Θх - Θ = Θ0 - XsinΘ. (2-15)
Из полученного выражения видно, что угол пролета электроном некоторого расстояния х-x1 изменяется в зависимости от момента его прихода в зазор модулятора, т. е. от фазы переменного напряжения Θ. Угол пролета замедленных электронов больше Θ0, а для ускоренных электронов Θд < Θ0.
Для дальнейшего анализа полезно знать зависимость времени tx пересечения электронами некоторой плоскости х от времени t пролета ими середины модулятора, т. е. от фазы модулирующего напряжения Θ. Эти зависимости представлены на рис. 2-3.
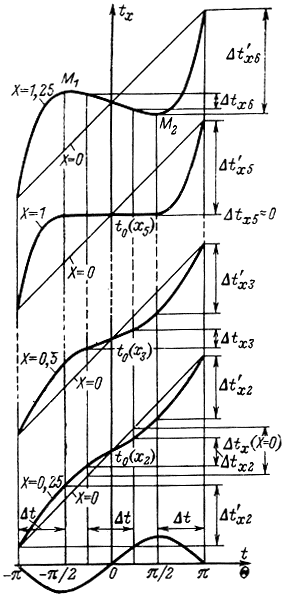
Рис. 2-3. Зависимость времени прихода электронов к плоскости х от фазы модулирующего напряжения
По оси абсцисс отложено время t пролета электронами середины зазора резонатора. Здесь же для сравнения времени с фазой модулирующего напряжения показана кривая переменного напряжения на второй сетке. По оси ординат отложено время tx пересечения электронами плоскости х. Когда переменное напряжение в модуляторе отсутствует (Х = 0), скорость электронов не изменяется и искомая зависимость для любого значения х изображается прямой линией с углом наклона 45°. Все электроны движутся равномерно, и если за время Δt через сетки прошло n электронов, то отрезок времени Δtх, в течение которого эти электроны пересекут плоскость х, расположенную на любом удалении от модулятора, будет таким же: Δt = Δtx, Предположим теперь, что к модулятору подведено переменное напряжение и, следовательно, Х > 0. Используя (2-14), можно записать:
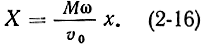
Отсюда видно, что при неизменном напряжении U0 на модуляторе и при фиксированной частоте параметр группирования X увеличивается с расстоянием х от модулятора.
Расположим плоскость х недалеко от модулятора, например на расстоянии х2 (рис. 2-2). Для х = х2 (Х = 0,25) зависимость tx = f(t) (рис. 2-3) изобразится кривой линией. Слева от оси ординат эта кривая идет выше прямой, так как электроны, пролетающие резонатор во время отрицательного полупериода на второй сетке, тормозятся, отстают от электрона, не изменившего свою скорость, и приходят к плоскости х2 позже. Наоборот, справа от оси ординат кривая идет ниже прямой, поскольку в этот отрезок времени электроны ускоряются в модуляторе и движутся быстрее электрона, служащего центром группирования. Эта зависимость показывает также, что внутри интервала группирования электронов (от -π/2 до +π/2) Δtx2 < Δt, т. е. электроны начинают собираться в сгустки. Слева и справа от этого интервала Δt'x2 > Δt и происходит разгруппирование электронов.
Если плоскость х отнести еще дальше от модулятора, например на расстояние х3, то описанные явления проявятся еще сильнее. Наконец, на расстоянии х5(Х = 1) кривая tx = f(t) в интервале от -π/2 до +π/2 идет почти параллельно оси абсцисс: dtх/dt ≈ 0. Происходит группирование электронов в очень плотный сгусток: время Δtх5 ≈ 0, все электроны, пролетевшие модулятор за время, соответствующее интервалу группирования (от -π/2 до +π/2), приходят к плоскости x5 почти одновременно*.
* (Группирование электронов в идеальный сгусток, приближающийся к δ-функции (Δt → 0), теоретически возможно при использовании модулирующего напряжения специальной пилообразной формы [8]:
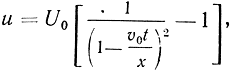
где х - расстояние от плоскости действия модулирующего напряжения до плоски образования сгустков.)
При дальнейшем удалении плоскости х зависимость все более искривляется. Появляются две точки М1 и М2, для которых dtx/dt = 0: сгусток электронов начинает раздваиваться и возникают два максимума плотности электронного потока в точках М1 и М2, которые при увеличении X раздвигаются все дальше.
Из рассмотренных зависимостей видно, что с расстоянием х изменение плотности электронного потока проявляется все сильней. При этом средняя плотность электронов за большой промежуток времени t ≥ T в любой плоскости х остается неизменной, так как число электронов не меняется и происходит лишь концентрация и разрежение электронного потока в различные интервалы времени.
Для вывода формулы, определяющей изменение электронного тока во времени, можно воспользоваться законом постоянства заряда. В самом деле, заряд в плоскости х должен быть таким же, как и в плоскости, проходящей через середину зазора модулятора:
|dqx| = |dq| (2-17)
или
|iexdtx| = |I0dt|, (2-18)
где iex - ток в плоскости х, I0 - ток в отсутствие модуляции.
Отсюда
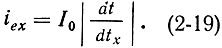
Производную dt/dtx легко получить, продифференцировав по времени выражение (2-12); проведя эту операцию и подставив результат в (2-19), получим:
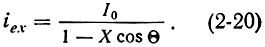
Отсюда видно, что параметр группирования X определяет амплитуду переменной составляющей электронного тока iex. При X ≤ 1 ток iex изменяется во времени по закону, близкому к гармоническому. Для случая Х = 1 знаменатель при Θ = 0 и cosΘ = 1 обращается в нуль, а ток iex устремляется в бесконечность, что соответствует идеальной группировке электронов. В действительности, конечно, iex ≠ ∞, так как в силу взаиморасталкивания электронов, различия их траекторий и других факторов группирование не является идеальным. При Х > 1 знаменатель выражения (2-20) дважды обращается в нуль, что соответствует образованию двух пиков плотности электронного потока.
Кривые изменения формы тока ie в зависимости от времени и расстояния представлены на рис. 2-4, иллюстрирующем рассмотренные выше процессы. При Х > 0,5 кривые iex(t) имеют несинусоидальный характер и поэтому богаты гармоническими составляющими.
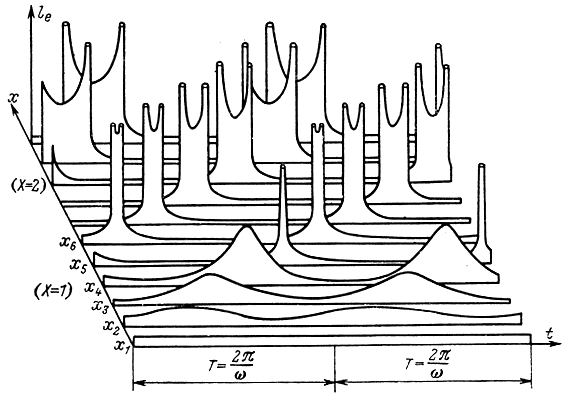
Рис. 2-4. Кривые изменения плотности электронного тока
Пользуясь анализом Фурье, выражение для тока можно записать в виде
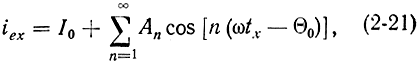
где
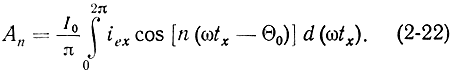
Перейдем от переменной tx к t Для этого, пользуясь выражением (2-19), определим d(ωtx) = d(ωt)I0/iex. Величина ωtх = Θx может быть легко получена из (2-15): Θх = Θ0 + Θ - XsinΘ.
Подставляя выражения для d(ωtx) и ωtx в (2-22), получим:
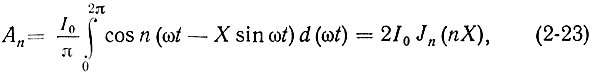
где Jn(nX) - функция Бесселя первого рода n-го порядка.
Таким образом,
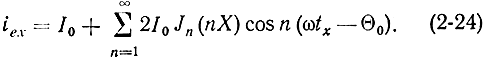
Так как в клистронных усилителях оба резонатора настраиваются на частоту ω усиливаемых колебаний, наибольший интерес представляет первая гармоника электронного тока, амплитудное значение которой легко получается из (2-24), если положить n = 1 и cos n(ωtх - Θ0) = 1:
Ie1M = 2I0J1(X). (2-25)
Максимальной величины амплитуда первой гармоники достигает при максимуме функции J1(X) (I0 = const), что, как видно из рис. 2-5, соответствует значению Х = 1,84*.
* (Для случая идеальных сгустков в виде δ-функции Ie1M = 2I0.)
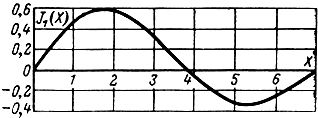
Рис. 2-5. График функции Бесселя первого рода
2-3. Взаимодействие электронного потока с переменным электрическим полем резонатора
Ток, наводимый в резонаторе. Рассмотрим более подробно процесс передачи энергии от электронного потока переменному электрическому полю резонатора. Предположим сначала, что через сетки улавливателя проходит сгусток электронов с зарядом - q (рис. 2-6). Пролетая зазор резонатора, электроны наводят на его сетках положительные заряды q1 и q2, сумма которых равна заряду сгустка электронов, а величины зарядов пропорциональны расстояниям от сгустка до сеток:
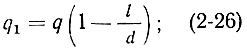
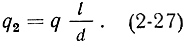
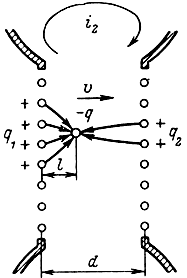
Рис. 2-6. Наведение зарядов на сетках резонатора при пролете электронов
За время Δt пролета электронов между сетками заряд q2 возрастает от нуля до q, а заряд q1 соответственно уменьшается до нуля. В теле резонатора в результате перемещения зарядов течет уравнительный (наведенный) ток от первой сетки ко второй, величина которого равна:
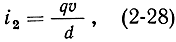
где υ - скорость пролета электрона через зазор резонатора, a d - расстояние между сетками.
По форме ток, наведенный сгустком электронов при υ = const, представляет собой прямоугольный импульс длительностью Δt, равной времени пролета электронов между сетками. Увеличение скорости движения электронов приводит к возрастанию импульса тока, а его длительность уменьшается; медленное движение электронов растягивает импульс тока и уменьшает его амплитуду. Однако при любом значении скорости сгустка электронов площадь импульса остается неизменной, численно равной заряду q.
Если в резонаторе существуют колебания, то наведенный ток для их поддержания должен способствовать перезаряду емкости контура. В случае тормозящего поля между сетками резонатора (рис. 2-7, а) в первой четверти периода (а-б) происходит заряд емкости и ток iк перезаряда уменьшается. Кривая тока контура изображена пунктирной линией. Наведенный ток i2 противоположен по направлению току iк и, таким образом, способствует его уменьшению, т. е. перезаряду емкости. Во второй четверти периода (б-в) происходит разряд емкости, ток контура меняет направление и увеличивается. Наведенный ток i2, совпадающий по направлению с током iк, помогает перезаряду емкости и поддерживает колебания в резонаторе. Во время существования ускоряющего поля (рис. 2-7, б) наведенный ток i2 в течение всего полупериода препятствует перезаряду емкости и, следовательно, облегчает затухание колебаний.
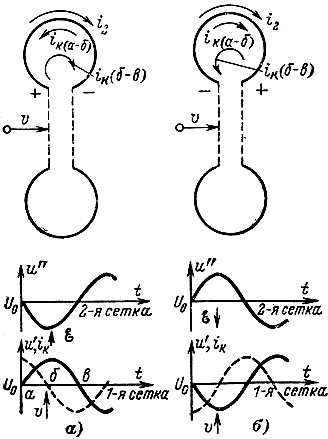
Рис. 2-7. Ток перезаряда емкости и наведенный ток в резонаторе клистрона. а - при пролете электронов в тормозящем поле; б - при пролете электронов в ускоряющем поле
Угол пролета электронов в пространстве дрейфа. Для того чтобы мощность, передаваемая электронным потоком второму резонатору, была наибольшей, необходимо, чтобы в момент прохождения электронами наиболее тормозящего поля поток был соответствующим образом сгруппирован (параметр Х = 1,84, что соответствует максимуму первой гармоники тока).
Для этого должны выполняться определенные фазовые соотношения между колебаниями в резонаторах и электронным током. Как видно из рис. 2-8, фазовый сдвиг между током ie, максимум которого соответствует точке Б - центру образуемого сгустка электронов, и напряжением u″1 на второй сетке первого резонатора равен ωt - π/2, где ωt - фаза, соответствующая максимуму напряжения u″1. При подлете к сеткам второго резонатора этот фазовый сдвиг равен ωt - π/2 + Θ0. Напряжение u″2 на второй сетке второго резонатора может отличаться по фазе от напряжения u″1 на любой угол Θ12.
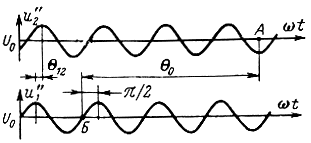
Рис. 2-8. К определению фазовых сдвигов между напряжением и током. A - время прихода сгустков во второй резонатор (максимально тормозящее поле); Б - центральный электрон сгустка (максимум тока ie)
Ко времени прилета сгустков к резонатору фаза напряжения u″2 будет ωt + 2πn + Θ12, где n = 1, 2, 3, ... Таким образом, разность фаз между током ie и напряжением u″2 равна Θ0 - 2πn - π/2 - Θ12. Сгусток электронов должен попадать в максимально тормозящее поле между сетками резонатора, т. е., как видно из рис. 2-8, ток ie должен отличаться по фазе от напряжения u″2 на величину π (точка А). Следовательно, должно выполняться условие Θ0 - 2π - π/2 - Θ12 = π. Отсюда ясно, что угол пролета невозмущенного электрона в пространстве дрейфа должен быть равен:
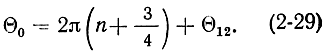
Эквивалентные схемы резонаторов клистрона. Схема для выходного резонатора представлена на рис. 2-9, а. Параллельно проводимости собственно резонатора
Yp2 = Gp2 + iBp2, (2-30)
состоящей из активной проводимости Gp2, характеризующей потери в резонаторе и реактивной составляющей, определяемой емкостью С2 и индуктивностью L2, включены также проводимость нагрузки
YН = Gн + iBН, (2-31)
пересчитанная к резонатору, и электронная проводимость
Ye2 = Ge2 + iBe2, (2-32)
обусловленная прохождением через зазор резонатора электронного потока.
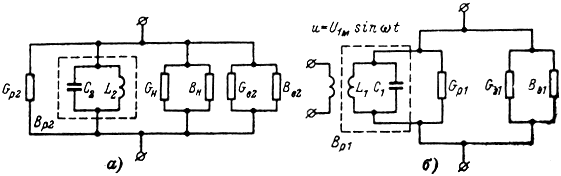
Рис. 2-9. Эквивалентные схемы выходного и входного резонаторов
Аналогичным образом, но без проводимости нагрузки YH может быть представлена схема входного резонатора (рис. 2-9, б).
2-4. Параметры и характеристики двухрезонаторного усилительного клистрона
Выходная мощность. Одним из важнейших параметров усилительного клистрона является мощность колебаний в нагрузке второго резонатора Pвых. Мощность колебаний Ре, развиваемая электронным потоком при оптимальных углах пролета (2-29), определяется простым соотношением, известным из электротехники:
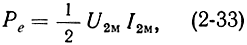
здесь U2M - амплитуда переменного напряжения на сетках выходного резонатора при установившихся колебаниях;
I2M = β2I2M (2-34)
- амплитуда наведенного тока в выходном резонаторе;
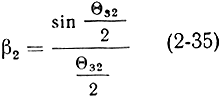
- коэффициент взаимодействия электронного потока с переменным полем на сетках второго резонатора (обычно β2 ≈ 0,6 ÷ 0,9); Θз2 - угол пролета электронов между сетками выходного резонатора.
Учитывая (2-25), выражение (2-33) можно переписать следующим образом:
Pe = β2I0U2MJ1(X). (2-36)
При X =1,84 имеем J1(X) = 0,58 и мощность Ре максимальна:
Pe макс = 0,58β2I0U2M. (2-37)
Выходная мощность, т. е. мощность, выделяемая в нагрузке, равна:
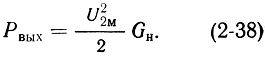
На основании эквивалентной схемы (рис. 2-9, а) для амплитуды напряжения на сетках второго резонатора можно записать:
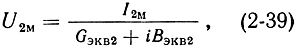
где
Gэкв2 = Gp2 + Gн + Ge2 (2-40)
и
Bэкв2 = Вр2 + Bн. (2-41)
Реактивной проводимостью Ве2 в случае точного выполнения условия (2-29) можно пренебречь.
Таким образом, используя (2-25), (2-34) и (2-39), выражение (2-38) можно записать в виде
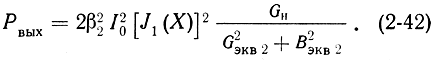
Отсюда следует, что величина выходной мощности зависит не только от правильного выбора соотношения проводимостей нагрузки и второго резонатора, но также от величины тока в клистроне и условий группирования электронного потока. Последнее обстоятельство свидетельствует о том, что уровень выходной мощности во многом определяется режимом модуляции электронного потока во входном резонаторе, а также условиями движения электронов в пространстве дрейфа. Поэтому задача о выборе режима работы клистрона для обеспечения максимальной величины Рвых решается наилучшим образом в сочетании с другой важной задачей - о коэффициенте усиления клистрона.
Коэффициент усиления клистрона по мощности обычно выражают в децибелах
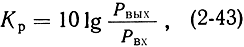
здесь величина Рвых определяется соотношением (2-42), а
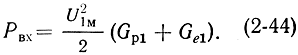
Используя соотношения (2-8) и (2-14), запишем это выражение в виде
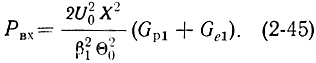
Подставляя (2-42) и (2-45) в (2-43), получим:
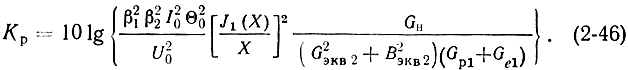
Анализ этого выражения показывает, что максимальной величины коэффициент усиления достигает при согласовании нагрузки с выходным резонатором клистрона (Вэкв2 = 0; Gэкв2 = 2Gн), а также при условии малости входного сигнала [X ≤ 1 и J1(X) ≈ Х/2].
Амплитудная характеристика клистрона. Пользуясь выражениями (2-42) и (2-45) для входной и выходной мощностей клистрона, можно построить весьма важную зависимость Рвых = f(Рвх) - амплитудную характеристику усилительного клистрона, а также кривую зависимости KP = f(Pвx) (рис. 2-10). Из этих кривых видно, что усилитель на клистроне может быть использован как в режиме максимального усиления (область малых входных сигналов, когда Х ≤ 1), так и в режиме максимальной выходной мощности, соответствующему значению Х = 1,84, когда амплитуда первой гармоники тока имеет наибольшую величину. При малых сигналах электронный поток, проходящий сетки второго резонатора, недогруппирован и мощность колебаний, развиваемых в нагрузке, меньше величины Рвых.макс. Снижение выходной мощности наблюдается и при слишком больших входных сигналах, когда электронный поток проходит сетки второго резонатора перегруппированным (Х > 1,84).
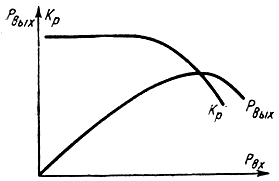
Рис. 2-10. Амплитудная характеристика двухрезонаторного усилительного клистрона
Полоса рабочих частот. В усилительном режиме оба резонатора клистрона настраиваются на частоту усиливаемых колебаний. Добротности объемных резонаторов достаточно высоки, и их полоса пропускания, измеряемая обычно по уровню снижения максимальной мощности на 3 дб, т. е. по уровню 0,5 Рвых.макс составляет доли процентов от резонансной частоты.
Таким образом, двухрезонаторный клистрон может использоваться лишь для усиления синусоидальных сигналов либо для усиления сигналов с нешироким спектром частот. Некоторое расширение рабочей полосы частот может быть достигнуто за счет увеличения связи выходного резонатора с нагрузкой, однако при этом неизбежно снижаются уровень выходной мощности и коэффициент усиления.
Электронный коэффициент полезного действия усилительного клистрона определяется как отношение мощности, развиваемой в выходном резонаторе, к мощности, расходуемой от источника постоянного напряжения:
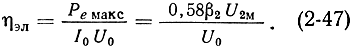
Амплитуда переменного напряжения обычно меньше или, в крайнем случае, может быть равна постоянному напряжению U2М ≤ U0. В противном случае в момент отрицательного полупериода на первой сетке выходного резонатора мгновенное напряжение окажется меньше нуля (-U2M + U0 < 0), электроны потеряют скорость и будут возвращаться к первому резонатору. Максимальное значение β2 = 1 при условии, что угол пролета Θ32 = 0. Следовательно, максимальная величина к. п. д. для усилительного клистрона равна:
ηэл.макс = 58%. (2-48)
Реальная величина ηэл из-за оседания части электронов на электродах прибора, эффекта разгруппирования и других причин значительно ниже расчетной и не превышает нескольких процентов.
2-5. Двухрезонаторный частотоумножительный клистрон
В § 2-2 было показано, что при Х > 0,5 функция iex(t) имеет сложную форму и богата гармоническими составляющими. Получив выражение (2-24), мы интересовались лишь первой гармоникой тока, так как в усилительном и генераторном режимах оба резонатора клистрона настраиваются на одну и ту же частоту и на выходе выделяются колебания с частотой первой гармоники.
Используя двухрезонаторный клистрон в качестве умножителя частоты, его второй резонатор настраивают на одну из высших гармоник. В этом случае наибольший интерес представляют те гармоники тока ie, которые выделяются выходным резонатором.
Устройство частотоумножительного клистрона аналогично устройству усилительного клистрона. Отличие заключается лишь в том, что частота колебаний, наводимых в выходном резонаторе, не равна частоте колебаний, подводимых от внешнего источника. Естественно, что и оптимальный режим работы умножителя частоты отличается от режима усилительного клистрона.
Максимальной величины первая гармоника электронного тока Достигает при Х = 1,84. Максимумы функций Бесселя высших порядков (рис. 2-11) соответствуют другим значениям X. Так, например, третья гармоника Iе3 имеет максимум при nХ = 4,2 или при Х = 1,4; пятая гармоника Iе5 - при Х = 1,28 и т. д.
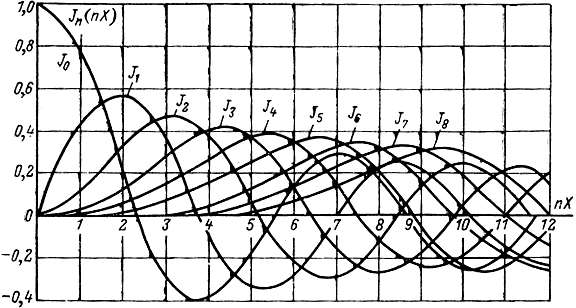
Рис. 2-11. Кривые функций Бесселя n-го порядка
Амплитуды высших гармоник, как это видно из табл. 2-1, сравнимы с величиной Ie1M.

Таблица 2-1
Это обстоятельство особенно важно для использования клистрона в качестве умножителя частоты, так как позволяет произвести умножение частоты при сравнительно небольшой потере мощности.
В реальных устройствах, однако, мощность выделяемых гармоник получается значительно меньше, поскольку проведенный анализ группирования электронного потока не учитывал ряд факторов (взаимного расталкивания электронов, разности их аксиальных скоростей и др.), влияющих на процесс группирования. Мощность колебаний частоты nω обычно на практике не превышает 10% от мощности колебаний частоты ω, подводимых ко входу.
Частоумножительные клистроны используются главным образом в тех случаях, когда требуется получение СВЧ колебаний высокой стабильности. Возбудителем умножителя служит стабилизированный кварцем генератор метровых волн. При коэффициенте умножения n = 10 и более на выходе умножителя могут быть получены высокочастотные колебания сантиметрового диапазона.
2-6. Многорезонаторный усилительный клистрон. Принцип действия
Устройство. Для усиления СВЧ колебаний используются также клистроны, содержащие несколько резонаторов. Наиболее часто применяются трех- и четырехрезонаторные клистроны. Они служат усилителями слабых сигналов, когда переменное напряжение на сетках группирователя оказывается недостаточным для эффективного группирования мощного электронного потока. Рассмотрим для примера устройство и принцип действия трехрезонаторного усилительного клистрона (рис. 2-12). К первому, входному резонатору подводятся колебания, подлежащие усилению. После усиления они отводятся из выходного резонатора. Промежуточный резонатор служит для дополнительного группирования электронного потока.
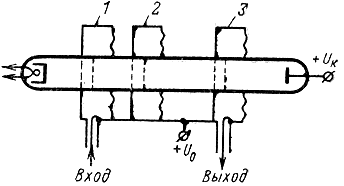
Рис. 2-12. Устройство трехрезонаторного клистрона. 1 - входной резонатор; 2 - промежуточный резонатор; 3 - выходной резонатор
Принцип действия. Под воздействием переменного напряжения на сетках первого резонатора электронный поток модулируется по скорости. Однако ввиду малости этого напряжения коэффициент модуляции М невелик и к сеткам второго резонатора электронный поток приходит недогруппированным (Х < 1). Второй резонатор, настраиваемый на ту же частоту, что и модулятор, не нагружен и поэтому обладает большим резонансным сопротивлением. Небольшие токи, наводимые в нем электронным потоком, развивают между сетками значительное по величине переменное напряжение. Это напряжение оказывает дополнительное модулирующее действие на поток. Третий резонатор располагается на таком расстоянии от второго, чтобы сгустки электронов проходили через его зазор при оптимальном параметре группирования. Таким образом, трехрезонаторный клистрон эквивалентен каскадному включению пары двухрезонаторных клистронов, так как сочетания первого и второго и второго и третьего резонаторов можно представить в виде двух последовательно включенных двухрезонаторных клистронов. Отличие заключается лишь в том, что в качестве выходного резонатора первого клистрона и входного резонатора второго клистрона используется один и тот же промежуточный резонатор. Этот резонатор, не будучи нагруженным, обладает большой добротностью, и поэтому потери энергии в нем меньше, чем в двух резонаторах при последовательном включении двух клистронов. Кроме того, в трехрезонаторном клистроне отсутствуют потери энергии, неизбежные при передаче сигнала с выхода одного клистрона ко входу другого. Поэтому коэффициент усиления трехрезонаторного клистрона оказывается больше коэффициента усиления, который можно было бы получить от двух последовательно включенных двухрезонаторных клистронов.
Помимо указанного преимущества, трехрезонаторные клистроны имеют более высокий к. п. д. Мощность, потребляемая таким клистроном от источника постоянного напряжения, расходуется лишь на создание общего электронного потока, в то время как при каскадном включении мощность затрачивается на образование электронного потока в каждом клистроне. Кроме того, двойная модуляция электронного потока несколько изменяет процесс группирования электронов и доля первой гармоники в электронном потоке увеличивается примерно на 15%.
2-7. Группирование электронов в многорезонаторном клистроне
Пространственно-временная диаграмма группирования электронов в трехрезонаторном клистроне показана на рис. 2-13. Как и на рис. 2-2, графики движения электронов представлены в координатах расстояние - время прямыми линиями, тангенс угла наклона которых к оси абсцисс пропорционален скорости их движения. Ордината х0 соответствует плоскости ускоряющего электрода; х1 - плоскости, проходящей через середину зазора первого резонатора; а ордината х2 - плоскости в середине второго резонатора. На диаграмме, кроме того, показаны кривые изменения сверхвысокочастотного напряжения u1 и u2 на сетках первого и второго резонаторов соответственно.
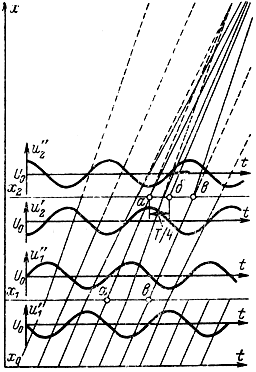
Рис. 2-13. Пространственно-временная диаграмма группирования электронов в трехрезонаторном клистроне
В пространстве х0 - x1 все электроны движутся с одинаковой скоростью, определяемой величиной ускоряющего напряжения U0. Под воздействием переменного напряжения на сетках первого резонатора происходит модуляция электронного потока по скорости так же, как и в двухрезонаторном клистроне. Центром сгустка электронов здесь также служит невозмущенный электрон а, минующий середину зазора первого резонатора в тот момент, когда напряжение на его второй сетке проходит через нуль, меняясь от минимума к максимуму.
В силу того, что амплитуда сигнала, подлежащего усилению и модулирующего электронный поток по скорости, невелика, электроны приходят к плоскости х2 второго резонатора недогруппированными: сгустки электронов неплотные и параметр группирования Х < 1. Проходя через сетки второго резонатора, настроенного на частоту сигнала, электроны возбуждают в нем колебания с частотой ω. Фаза этих колебаний такова, что в момент прохождения сгустка электронов поле между сетками резонатора тормозящее (см. § 2-3). Возникшее в зазоре второго резонатора сверхвысокочастотное электрическое поле модулирует электронный поток по скорости, причем этот процесс сопровождается смещением центра сгустка на четверть периода.
Графики движения электронов за плоскостью х2 без учета воздействия поля второго резонатора показаны пунктиром. В результате воздействия поля второго резонатора движение электронов за плоскостью х2 изменяется (сплошные линии) и, как это видно из рис. 2-13, группирование электронов после их пролета через зазор второго резонатора будет происходить вокруг электрона б, проходящего середину зазора в тот момент, когда напряжение на второй сетке равно нулю, при изменении от минимума к максимуму. Этот электрон проходит зазор второго резонатора на Т/4 позже электрона а, служившего центром сгустка в пространстве дрейфа между первым и вторым резонаторами. Теперь в сгусток включаются не только все электроны, ранее группировавшиеся возле электрона а, но даже электрон в, находившийся ранее в центре разрежения электронного потока.
В результате в пространстве дрейфа за вторым резонатором будет происходить перегруппирование электронного потока и кривые изменения плотности электронного тока будут отличаться от приведенных на рис. 2-4. Иначе говоря, за счет влияния поля в зазоре промежуточного резонатора существенно повышается эффект группирования по сравнению с тем эффектом, который мог бы быть Достигнут на той же длине дрейфа (между первым и третьим резонаторами), но в отсутствие промежуточного резонатора.
Физически повышение эффекта группирования можно объяснить с помощью кривых зависимости tx = f(Θ) времени прихода электронов к плоскости середины зазора выходного резонатора от фазы модулирующего напряжения. На рис. 2-14 показаны: внизу - кривая изменения напряжения на второй сетке первого резонатора; на среднем графике - кривая tx = f(Θ) при Х ≈ 2 для случая отсутствия промежуточного резонатора; на верхнем графике - та же кривая, но в случае дополнительной модуляции в зазоре промежуточного резонатора.
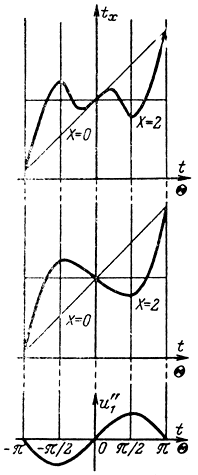
Рис. 2-14. Зависимость времени прихода электронов к плоскости х от фазы модулирующего напряжения
Из этого рисунка видно, что в первом случае кривая ie(t) имеет два максимума (см. рис. 2-3 и 2-4), а во втором - четыре. Иначе говоря, закон изменения плотности электронного тока во времени приближается к идеальному (к образованию бесконечно плотных сгустков, длящихся бесконечно малое время), который теоретически может быть получен при использовании пилообразного модулирующего напряжения специальной формы.
Вследствие изменения формы электронных сгустков амплитуда первой гармоники электронного тока при каскадном группировании может быть значительно больше величины Iе1M = 1,164 I0, получаемой в двухрезонаторном клистроне [см. (2-25) и рис. 2-5], и достигать значения 1,48 I0.
Влияние настройки промежуточного резонатора. При рассмотрении пространственно-временной диаграммы каскадного группирования (рис. 2-13) уже отмечалось, что при настройке промежуточного резонатора на частоту усиливаемого сигнала переменное напряжение на его сетках, возникающее за счет наведенного тока, обусловленного прохождением сгустка электронов, находится в фазе с электронным током. При этом центр сгустка во втором пространстве дрейфа смещается на угол Ψ = π/2. Если промежуточный резонатор расстроить относительно частоты ω усиливаемого сигнала, а значит, и частоты следования сгустков, то напряжение в зазоре резонатора окажется сдвинутым по фазе относительно электронного тока, питающего контур, на некоторый угол φ. Величина этого фазового сдвига зависит от степени расстройки, а его знак - от соотношения ωр/ω частот настройки резонатора и частоты сигнала. В случае ωр/ω < 1, т. е. при настройке резонатора на более низкую частоту, его проводимость будет иметь емкостный характер, угол φ будет лежать в пределах от 0 до -π/2, кривые напряжения на рис. 2-13 как бы сместятся влево и сгусток электронов придет в зазор промежуточного резонатора в тот полупериод, когда напряжение на сетках способствует разгруппированию электронов. И наоборот, если резонатор настроен на более высокую частоту (ωр/ω > 1), его проводимость имеет индуктивный характер и кривые напряжения (рис. 2-13) как бы сместятся вправо (φ будет лежать в пределах от 0 до +π/2). Сгусток электронов попадает в зазор промежуточного резонатора в ту часть периода, когда напряжение на его сетках оказывает на электронный поток группирующее воздействие. Очевидно что наибольший группирующий эффект за счет поля в зазоре промежуточного резонатора будет наблюдаться при условии, что φ ≈ +π/2. При этом группирование во втором пространстве дрейфа будет происходить вокруг того же электрона а, который служит центром сгустка в первом пространстве дрейфа (см. рис. 2-13).
Однако следует помнить, что при расстройке промежуточного резонатора происходит не только изменение фазового угла между напряжением и током; при этом уменьшается и амплитуда U2M (напряжения в зазоре резонатора.
В клистронах с числом резонаторов больше трех для повышения выходной мощности производят обычно расстройку предпоследнего резонатора.
2-8. Характеристики и параметры многорезонаторных усилительных клистронов
Для многорезонаторных клистронов используются те же параметры и характеристики, что и для двухрезонаторного клистрона усилителя.
Выходная мощность. Для определения этой величины можно воспользоваться соотношением (2-42), подставив туда величины, характерные для многорезонаторного клистрона:
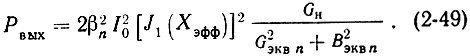
Здесь βn - коэффициент эффективности взаимодействия электронов с полем выходного резонатора; Gэквn и Вэквn - активная и реактивная эквивалентные проводимости выходного резонатора; Xэфф - эффективный параметр группирования, оценивающий суммарный эффект модуляции электронного потока с учетом воздействия промежуточных резонаторов.
Входная мощность. Выражение (2-45) для входной мощности в случае многорезонаторного клистрона запишется в виде
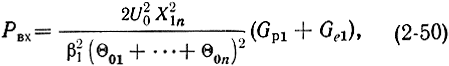
где Х1n - параметр группирования в пространстве между первым и последним резонаторами без учета воздействия полей промежуточных резонаторов; Θ0n - угол пролета в последнем промежутке дрейфа.
Коэффициент усиления. Используя (2-49) и (2-50) для коэффициента усиления можно записать:
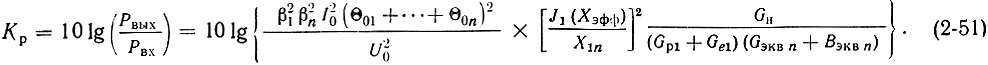
В многорезонаторных клистронах коэффициент усиления может быть весьма высоким, достигая нескольких десятков децибел, так как введение каждого промежуточного резонатора позволяет повысить величину Kр на 10-20 дб.
Амплитудная характеристика. Вид амплитудной характеристики многорезонаторного клистрона может изменяться в зависимости от настройки промежуточных резонаторов. Так, при синхронной настройке резонаторов (настройке всех резонаторов на частоту сигнала) амплитудная характеристика (рис. 2-15, кривая а) имеет максимум при малых величинах Рвх. В этом случае клистрон обладает высоким коэффициентом усиления и используется для максимального усиления очень слабых сигналов. В случае расстройки промежуточного или предоконечного резонатора (кривая б на рис. 2-15) коэффициент усиления клистрона значительно ниже, о чем свидетельствует более пологий характер кривой. В таком режиме в силу оптимальных условий группирования на выходе клистрона может быть получен сигнал наибольшей мощности.
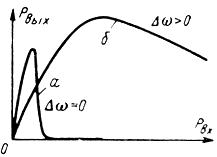
Рис. 2-15. Амплитудные характеристики трехрезонаторного клистрона
Электронный к. п. д. многорезонаторного клистрона может быть определен по формуле (2-47), которая в этом случае принимает вид:
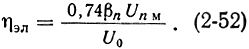
Здесь UnM - амплитуда переменного напряжения на сетках последнего резонатора.
При выполнении условия UnM ≤ U0, обсуждавшегося в § 2-4, и βn = 1 максимальная величина к. п. д. равна 74%.
Как уже отмечалось ранее, повышение к. п. д. объясняется эффективным группированием электронного потока, при котором форма электронного сгустка приближается к идеальной.
Особенности конструкции. Многорезонаторные клистроны применяются в различных радиотехнических системах в качестве усилителей слабых сигналов, а также для получения импульсных и непрерывных сигналов большой мощности в сантиметровом и дециметровом диапазонах волн. Наиболее распространены трех- и четырехрезонаторные клистроны, однако в некоторых типах усилительных клистронов число резонаторов достигает шести.
Мощные клистронные усилители позволяют получить на выходе сигналы мощностью в несколько сотен киловатт в непрерывном режиме и до нескольких десятков мегаватт в импульсном режиме. Коэффициент усиления трех- и четырехрезонаторных клистронов составляет 30-50 дб, а в шестирезонаторных клистронах достигает 60-70 дб. Коэффициент полезного действия многорезонаторных клистронов обычно лежит в пределах 35-45%.
Многорезонаторные клистронные усилители - обычно крупногабаритные устройства, снабженные мощными, высоковольтными источниками питания, Конструкция таких усилителей подчинена ряду весьма сложных требований, связанных с необходимостью обеспечения и формирования мощного электронного потока, отбором и рассеянием большой мощности, обеспечением высокой электрической прочности, необходимой при использовании ускоряющих напряжений, достигающих сотен киловольт.
Катоды многорезонаторных клистронов - обычно оксидные или импрегнированные - имеют вогнутую сферической формы активную поверхность, обеспечивающую начальную фокусировку электронного потока. В пролетных пространствах поток электронов, как правило, фокусируется с помощью электромагнитных катушек или постоянных магнитов. Иногда для фокусирования электронов используются специальные электростатические линзы.
Резонаторы, обычно в виде отрезков волновода, располагают либо внутри откачанного баллона, либо выполняются съемными и крепятся вне рабочего вакуумного пространства к специальным выводам.
В некоторых многорезонаторных клистронах, работающих в импульсном режиме, предусматривается, помимо ускоряющего электрода, специальный модулирующий анод, располагаемый ближе к катоду.
2-9. Отражательный клистрон. Принцип действия. Группирование электронов
Устройство. Отражательный клистрон имеет всего один резонатор, служащий одновременно модулятором и улавливателем энергии. Устройство отражательного клистрона показано на рис. 2-16. Здесь имеется катод, ускоряющий электрод и объемный резонатор. На некотором расстоянии за сетками резонатора расположен отражатель, на который подается отрицательное напряжение порядка Uотр ≈ -(100 ÷ 200) в.
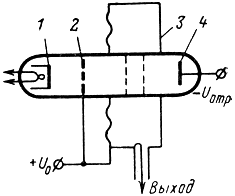
Рис. 2-16. Устройство отражательного клистрона. 1 - катод; 2 - ускоряющий электрод; 3 - резонатор; 4 - отражатель
Принцип действия. Поток электронов от катода, разгоняемый полем ускоряющего электрода, проходит через сетки резонатора. Вследствие флуктуации электронного потока в резонаторе наводятся слабые колебания. В результате дальнейших процессов, которые описаны ниже, электроны передают свою энергию высокочастотному полю резонатора, поддерживая возникшие колебания, амплитуда которых вскоре достигает стационарной величины.
Пространственно-временная диаграмма. В установившемся режиме поток электронов, движущихся через сетки резонатора (рис. 2-17), подвергается воздействию переменного электрического поля. Скорость электронов, как и в двухрезонаторном клистроне, изменяется в зависимости от мгновенного напряжения u = U0 + UMsinωt между сетками резонатора в соответствии с законом (2-9)
υ1 = υ(1 + Msinωt).
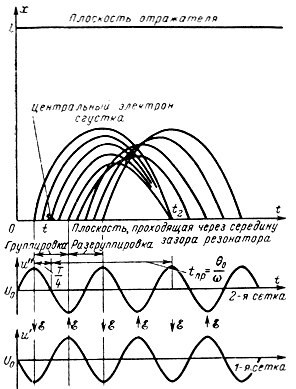
Рис. 2-17. Пространственно-временная диаграмма группирования электронов в отражательном клистроне
Пролетев сетки резонатора, электроны попадают в тормозящее поле отражателя. Постепенно замедляя движение, они теряют скорость до нуля в точке, где мгновенная разность потенциалов u + (-Uотр) = 0, и, отталкиваемые полем отражателя, движутся обратно к резонатору.
Электроны, пролетевшие резонатор в те отрезки времени, когда поле между его сетками ускоряющее (положительный полупериод на второй сетке), проникают дальше по направлению к отражателю. Те же электроны, которые пролетели резонатор в тормозящем поле (отрицательный полупериод на второй сетке), проникают в пространство за сетками на меньшую глубину. Как видно из рис. 2-17, поток электронов, возвращающихся к резонатору, во времени неравномерен по плотности. Модуляция электронов по скорости приводит к модуляции по плотности.
Электроны, прошедшие резонатор в ту половину периода, когда переменное напряжение на второй сетке изменялось от максимума к минимуму, образуют при возвращении к сеткам плотный сгусток. В следующий полупериод изменения скоростей электронов таковы, что они при возвращении разгруппировываются.
Центром образовавшегося сгустка является невозмущенный электрон, пролетевший резонатор, когда переменное напряжение на второй сетке проходило через нуль, меняясь от положительного к отрицательному, а не наоборот, как это было в двухрезонаторном клистроне (см. рис. 2-2).
Подобрав величины напряжений U0 и -Uотр, можно добиться, чтобы сгусток электронов приходил к сеткам резонатора в тот момент, когда поле в зазоре тормозящее. Вследствие того что вектор скорости возвращающихся электронов противоположен по направлению вектору скорости электронов, движущихся от катода, поле в зазоре будет для них тормозящим, когда напряжение на второй сетке положительное. Пролетая между сетками резонатора в тормозящем поле, сгусток электронов поддерживает возникшие в резонаторе колебания (см. § 2-3).
Закон изменения электронного тока. Пролетев сетки резонаторов, электроны движутся в пространстве отражателя до точки остановки равнозамедленно, а затем обратно к резонатору равноускоренно. Этот путь они проходят за время tпр = t2 - t, где t - время пролета середины резонатора на пути к отражателю, a t2 - время возвращения к резонатору.
Для пути, невозмущенного электрона к отражателю и обратно к резонатору можно написать:
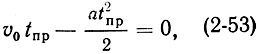
так как суммарный путь равен нулю.
Отсюда
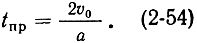
Корень tпр = 0 отвечает решению (2-53) для электронов, не вылетевших из резонатора.
Очевидно, для любого электрона с учетом (2-9) время пролета 1 равно:
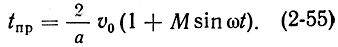
Величину ускорения легко определить, зная напряженность поля между резонатором и отражателем:
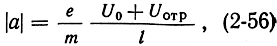
где l - расстояние между серединой зазора и отражателем.
Подставляя (2-56) в (2-54), получим:
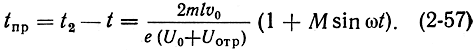
Умножим обе части этого равенства на ω:
Θпр = Θ2 - Θ = Θ0 + XsinΘ, (2-58)
где Θпр - угол пролета электронов от середины зазора к отражателю и обратно; Θ2 = ωt2 - фаза переменного напряжения в момент возвращения электронов в резонатор; Θ = ωt - фаза переменного напряжения в момент вылета электронов из резонатора;
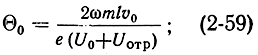
Θ0 - угол пролета невозмущенного электрона от резонатора к отражателю и обратно.
Пользуясь законом сохранения заряда |ie2dt| = |I0dt| и дифференцируя (2-57) по t, получим:
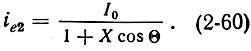
Это выражение отличается от (2-20) для двухрезонаторного клистрона лишь знаком перед косинусоидальным членом в знаменателе, что объясняется сдвигом центра группирования в отражательном клистроне по сравнению с двухрезонаторным на π (сравните рис. 2-2 и 2-17).
Гармонический анализ выражения (2-60), так же как и для двухрезонаторного клистрона, приводит к известной формуле (2-25) для амплитуды первой гармонической составляющей электронного тока
Ie1М = 2I0J1(X).
Таким образом, хотя процесс группирования электронов в отражательном клистроне отличен от процесса группирования в двухрезонаторном клистроне, функция (2-58) отличается от (2-15) лишь знаком при переменной составляющей, что не изменяет спектрального состава электронного тока.
2-10. Баланс фаз и баланс мощности в отражательном клистроне
Условия генерирования незатухающих колебаний для отражательного клистрона, как и для любого другого генератора, определяются балансом фаз и балансом амплитуд (мощности).
Баланс фаз в отражательном клистроне выполняется при условии, что сгусток электронов приходит из пространства отражения к сеткам резонатора в тот момент, когда высокочастотное поле между сетками тормозящее.
Ток в отражательном клистроне, т. е. центральный электрон будущего сгустка, отстает по фазе от напряжения u″ на второй сетке на π/2 (рис. 2-17). Если фаза напряжения u″ в момент t равна ωt, то фаза тока в этот же момент ωt + π/2. К моменту t2 возвращения электронов к резонатору фаза тока равна:
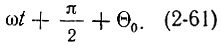
Сгусток электронов должен попасть в максимально тормозящее поле, и, следовательно, фаза тока должна быть равна фазе напряжения u″, которая к моменту t2 равна ωt + 2πn. Из этого условия получаем:
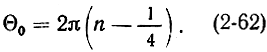
Угол Θ0 согласно (2-59) зависит от U0 и Uотp. Меняя эти напряжения, можно получить различные углы пролета Θ0, соответствующие разным величинам n = 1, 2, 3...
На рис. 2-18 изображены графики движения невозмущенного электрона и крайних электронов, образующих сгусток, при различных напряжениях Uотp.
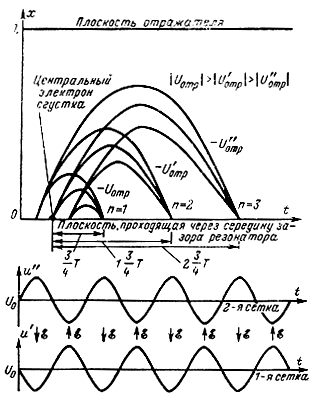
Рис. 2-18. Пространственно-временная диаграмма. Группирование электронов при различных Θ0
Приравнивая (2-59) и (2-62), подставляя
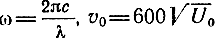
численные значения величин с, е и m, получим:
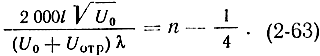
Области колебаний. Соотношение (2-63), определяющее баланс фаз в отражательном клистроне, позволяет, зная l, n и λ, подобрать необходимые величины U0 и Uотр. Из (2-63) следует, что клистрон генерирует колебания лишь при целочисленных значениях т, т. е. при таких углах пролета, когда сгусток электронов, возвращаясь, попадает в максимум тормозящего поля. В действительности (рис. 2-18), генерация может возникнуть и в случае небольших отклонений ΔΘ0 от величины 2π (n - 1/4). Электроны все же попадают в тормозящее поле, хотя его величина и меньше максимальной. Мощность колебаний уменьшается.
Таким образом, при плавном изменении U0 или Uотр генерация наблюдается лишь в определенных интервалах изменения этих величин, когда точно или приближенно выполняется условие ()2-63.
В соответствии с этим различают области или зоны генерации отражательного клистрона, соответствующие различным значениям числа n (рис. 2-19).
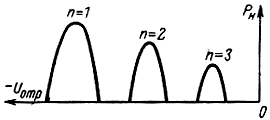
Рис. 2-19. Области генерации
Баланс мощности. Процесс передачи энергии от электронного потока электрическому полю резонатора аналогичен рассмотренному выше (§ 2-3) для двухрезонаторного клистрона. Сгруппированные электроны, возвращаясь к сеткам резонатора, в тормозящем поле передают энергию электрическому полю, способствуя перезаряду емкости контура и поддерживая возникшие в нем колебания.
Проходя через сетки резонатора, сгусток электронов наводит в контуре ток, амплитуда которого с учетом (2-25) равна:
I1M = βIe1M = 2βI0J1(X), (2-64)
где β = β1 определяется выражением (2-6).
В центре зоны генерации напряжение u″ и электронный ток находятся в фазе; мощность, передаваемая электронным потоком резонатору, равна:
Pe = βI0U1мJ1(X), (2-65)
где U1м - амплитуда переменного напряжения на сетках резонатора.
Часть этой мощности расходуется на восполнение потерь в самом резонаторе, а остальная мощность отводится в нагрузку
Ре = Рп + Рн. (2-66)
Здесь
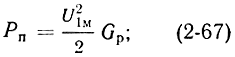
Рп - мощность потерь; Gp - проводимость резонатора;
| Pн = | U21M | Gн; (2-68) |
| 2 |
Pн - мощность, выделяемая в нагрузке; Gн - проводимость нагрузки.
Таким образом,
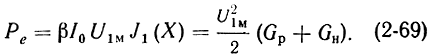
Определим величину U1м из (2-8) с учетом (2-14)
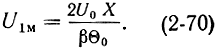
Подставляя (2-70) в (2-65), получим:
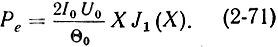
Отсюда видно, что при заданном токе катода I0 и постоянном U0 величина Ре является функцией X. Зависимость XJ1(X) = f(X) показана на рис. 2-20. Максимум Ре соответствует Х = 2,4. Это объясняется тем, что при Х = 2,4 пики электронного тока оказываются раздвинутыми во времени примерно на величину T/3 (рис. 2-4). Если при этом невозмущенный электрон приходит в резонатор в момент максимума тормозящего поля, то наиболее уплотненные сгустки электронов проходят через резонатор несколько раньше и несколько позже наступления U1м. При этом наведенный ток имеет два максимума, соответствующих по времени наибольшей скорости изменения тока iK перезаряда емкости С (рис. 2-7). Эти условия отвечают наиболее эффективной передаче мощности от электронов в резонатор.
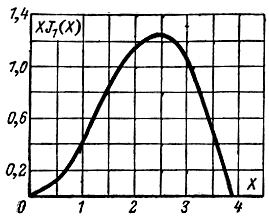
Рис. 2-20. График функции XJ1(X) от X
Из выражения (2-71) следует также, что с увеличением Θ0, т. е. с переходом к зонам генерации с большими n, электронная мощность в центре зоны падает. Это объясняется следующим образом. Угол Θ0, например, при n = 3 больше, чем в случае n = 1 (см. рис. 2-18). Группирование электронов в третьей зоне, следовательно, происходит на большем пути. Поэтому разность скоростей ускоренного и замедленного электронов, а значит, и величина U1м должны быть меньше. Оптимальное значение параметра Х = 2,4 для центра любой зоны должно быть неизменным. Нужное напряжение U1м на сетках при переходе в другую зону за счет, например, изменения Uотр устанавливается автоматически.
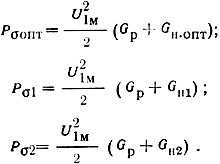
Для определения величины U1м, при которой выполняется баланс мощности, рассмотрим зависимости электронной мощности, мощности потерь и мощности в нагрузке от этого напряжения (рис. 2-21). Кривые Pe = f(U1м) (2-71) и Pп = f1(U1м) (2-67) построены для резонатора, проводимость потерь которого известна. Если на график нанести кривую
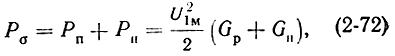
то точка пересечения этой параболы с кривой Pe = f(U1м) и определит баланс мощности: будет выполнено условие (2-66). На рисунке показаны три кривые Pσ = f(U1м) при Gн.опт, Gн1 < Gн.опт и Gн2 > Gн.опт.
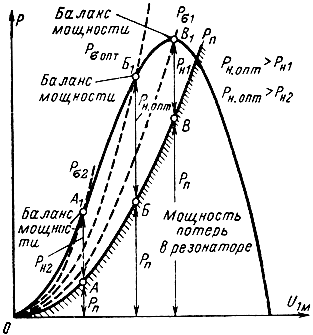
Рис. 2-21. Баланс мощности в отражательном клистроне. Зависимость полезной мощности Рн от величины нагрузки
Отрезки прямых между точками А1, Б1, В1 и точками A, Б, В на кривой Pп = f1(U1м) соответствуют мощностям, выделяемым в нагрузке для трех рассмотренных случаев. При уменьшении или увеличении Gн относительно Gн.опт мощность в нагрузке уменьшается.
Пользуясь рассмотренными кривыми, можно объяснить и то, что наибольшая мощность в нагрузке не всегда получается в центре первой зоны.
На рис. 2-22 построены кривые Pe = f(U1м) для первой, второй и третьей зон. С увеличением n максимальное значение мощности Ре уменьшается, однако потери в резонаторе настолько велики, что наибольшая мощность в нагрузке получается во второй зоне (рис. 2-23).
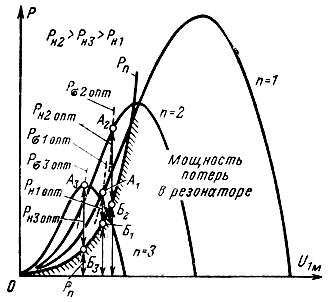
Рис. 2-22. Изменение мощности Рн.опт в различных областях при больших потерях в резонаторе
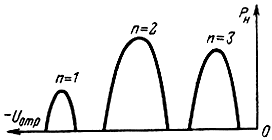
Рис. 2-23. Области генерации в случае резонатора с большими потерями
2-11. Условие самовозбуждения
Отражательный клистрон представляет собой автогенератор, колебания в котором возникают обычно в режиме мягкого самовозбуждения. Условия самовозбуждения зависят от параметров резонатора, нагрузки и электронного режима клистрона.
Эквивалентная схема отражательного клистрона (рис. 2-24) содержит активные и реактивные проводимости собственно резонатора и нагрузки, а также электронную проводимость.
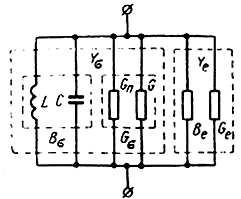
Рис. 2-24. Эквивалентная схема резонатора клистрона с учетом электронной проводимости
Закон изменения электронной проводимости. В § 2-10 было показано (2-61), что электронный ток отстает от напряжения на сетках резонатора на угол Θ0 + π/2. Следовательно, для электронной проводимости можно записать:
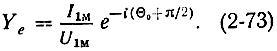
Знак минус свидетельствует об изменении направления тока при подлете электронов к резонатору. Подставляя сюда (2-64), пользуясь формулой Эйлера eiα = cosα - isinα и проводя тригонометрические преобразования, получим:
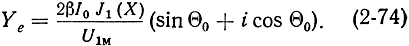
Это выражение, используя (2-70), можно записать и в другой форме:
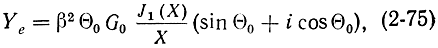
гдe G0 = I0/U0.
Отсюда видно, что при увеличении во активная электронная проводимость изменяется по закону синуса, а реактивная - по закону косинуса, причем амплитуды той и другой функции линейно возрастают (рис. 2-25). В интервалах от π до 2π, от 3π до 4π и т. д. активная электронная проводимость отрицательна, что свидетельствует о возможности генерации.
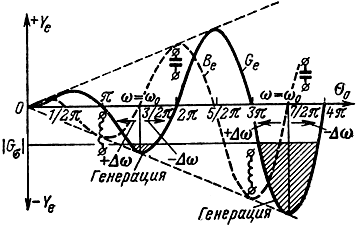
Рис. 2-25. Зависимость активной и реактивной составляющих электронной проводимости от угла пролета
Условие самовозбуждения для схемы на рис. 2-24 можно записать в виде равенства нулю суммы активных и реактивных проводимостей:
Ge + Gp + Gн = 0; (2-76)
Ве + Вσ = 0. (2-77)
Подставляя вещественную часть выражения (2-74) в (2-76), получим:
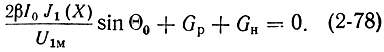
При Θ0 = 2π(n - 1/4)sinΘ0 = -1, и это выражение принимает вид:
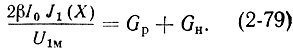
Умножив (2-79) на U1м2/2, получим соотношение (2-69) для баланса мощности в центрах зон генерации.
Абсолютная величина Gσ = Gp + Gн отложена на графике рис. 2-25 по оси отрицательных проводимостей. При условии Ge + Gp + Gн = 0 возникают колебания с постоянной амплитудой. Если
|Ge| > Gp + Gн, то амплитуда колебаний нарастает до тех пор, пока согласно (2-70) Ge не уменьшится до величины Gp + Gн.
Пусковой ток. Условие самовозбуждения на основании (2-76) и учитывая, что для режима очень малых амплитуд J1(Х)/Х ≈ 1, можно записать в виде:
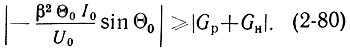
Перепишем это уравнение относительно тока I0, использовав выражение (2-62) и полагая при этом sinΘ0 = -1:
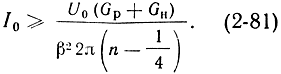
Величина тока I0, при которой выполняется условие (2-81), называется пусковым током lH. Из выражения (2-81) видно, что возникновение генерации в отражательном клистроне для данного резонатора и при заданной нагрузке наблюдается лишь при условии, что I0 > Iп. Кроме того, самовозбуждение облегчается с уменьшением U0 и с увеличением номера зоны, что и понятно, так как для областей с большими значениями n требуется меньшая амплитуда колебаний.
Электронный гистеризис. В некоторых случаях форма кривых Pн = f(Uотр), показанных на рис. 2-19 или 2-23, нарушается; появляются резкие изменения мощности колебаний, причем при различных значениях Uотр в зависимости от того, меняется ли напряжение на отражателе от нуля в сторону отрицательных величин или же в обратном направлении (рис. 2-26). Это явление, носящее наименование электронного гистерезиса, объясняется рядом различных причин, среди которых основная связана с многократным прохождением электронов через сетки резонатора. Электроны, прошедшие зазор после возвращения из пространства отражения, могут вновь изменить направление своего движения и пройти через сетки резонатора еще раз. Следствием этого процесса является изменение характера зависимости Ge от амплитуды переменного напряжения, которая при обычных условиях имеет монотонный характер. В случае многократного прохождения электронов через зазор резонатора в этой зависимости появляется максимум, в результате чего условия самовозбуждения нарушаются. Электронный гистерезис - вредное явление в отражательных клистронах, осложняющее их использование в радиотехнических устройствах. Для устранения электронного гистерезиса несколько изменяют конфигурацию сеток резонатора и отражателя с тем, чтобы большая часть электронов, прошедших зазор резонатора повторно, оседала на элементах резонатора.
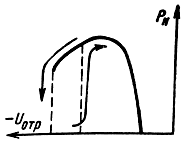
Рис. 2-26. Форма области генерации при гистерезисе
Электронный к. п. д. отражательного клистрона ηэл характеризуется отношением полезной мощности Ре, развиваемой электронным потоком к мощности P0 = I0U0, потребляемой от внешнего источника питания.
Выражение для ηэл легко получить, разделив (2-71) на величину P0 и подставляя туда (2-62):
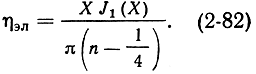
Отсюда следует, что ηэл падает с номером области n и в любой области достигает наибольшего значения при максимуме функции XJ1(X), что соответствует величине Х = 2,4 (см. рис. 2-20).
В реальных устройствах далеко не вся мощность Ре отводится в нагрузку, значительная часть мощности теряется в самом резонаторе, в линиях отвода энергии и т. д. Поэтому полный к. п. д. клистрона η обычно не превышает нескольких процентов.
2-12. Электронная настройка частоты
Весьма ценным свойством отражательного клистрона является зависимость частоты генерируемых колебаний от напряжений на электродах прибора. Пределы изменения частоты невелики (около 1% от средней рабочей частоты), но даже такая возможность электронного управления частотой колебаний позволяет с успехом использовать отражательный клистрон в приемниках СВЧ диапазона в качестве гетеродина, частота которого автоматически подстраивается под частоту сигнала. Обычно в отражательных клистронах изменяют частоту путем регулировки напряжения на отражателе, так как в цепи питания этого электрода не течет ток.
Рассмотрим это явление, пользуясь пространственно-временной диаграммой (рис. 2-27), иллюстрирующей изменение движения электронов при небольших отклонениях напряжения - Uотр от оптимальной величины. Кривые а, б и в соответствуют оптимальной величине - Uотр; сгусток электронов приходит в резонатор в тот момент времени t0, когда поле резонатора максимально тормозящее. Максимум электронного тока совпадает по времени с максимумом переменного напряжения на второй сетке резонатора. Иначе говоря, ток, питающий контур (электронный ток), совпадает по фазе с напряжением на контуре. Эти условия отвечают резонансу колебательной системы; проводимость контура имеет чисто активный характер, и частота колебаний равна резонансной частоте контура. Если напряжение - Uотр изменить на некоторую величину, сделать его более отрицательным, то электроны будут проникать в пространство отражения на меньшую глубину (кривые а', б', в') и сгусток электронов придет к сеткам резонатора на время Δt раньше, чем напряжение u″ достигнет максимума. Электронный ток, питающий контур, опередит напряжение на нем, проводимость резонатора станет емкостной, и частота генерируемых колебаний увеличится. При уменьшении отрицательного напряжения на отражателе частота колебаний в контуре уменьшится, так как электроны глубже проникнут к отражателю, электронный ток отстанет от напряжения в зазоре и проводимость контура будет иметь индуктивный характер.
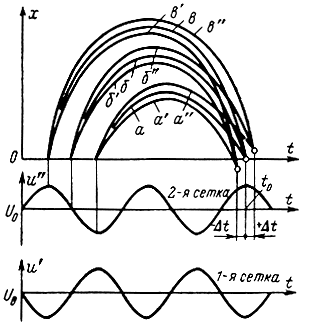
Рис. 2-27. Пространственно-временная диаграмма, поясняющая принцип электронной настройки частоты
Обратимся снова к рис. 2-25, из которого видно, что в интервалах от π/2 до 3π/2, от 5π/2 до 7π/2 и т. д. реактивная электронная проводимость имеет индуктивный характер, а в промежутках между этими интервалами - емкостный характер.
Частота колебаний в клистроне определяется соотношением реактивных проводимостей. Полагая нагрузку чисто активной (Вн = 0), используя мнимую часть выражения (2-74), перепишем (2-77) в виде
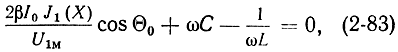
где
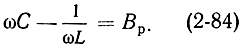
При Θ0 = 2π(n - 1/4)cosΘ0 = 0 и, следовательно,
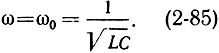
Частота колебаний равна резонансной частоте ω0 контура.
При отклонении угла Θ0 от значений 2π(n - 1/4) условие (2-85) нарушается. Если уменьшить угол Θ0, увеличив отрицательное напряжение на отражателе, то, как видно из рис. 2-25, Ве будет иметь индуктивный характер, а Вр согласно (2-77) должна быть емкостной, что приводит, как это отмечалось выше, к увеличению частоты колебаний. И наоборот, при увеличении Θ0 проводимость Ве становится емкостной, Вр - индуктивной и частота уменьшается.
Закон изменения частоты. Положим, что угол пролета изменился на величину
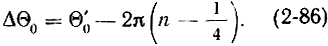
Это вызовет изменение частоты на величину Δω. При условии, что Δω мало (Δω/ω0 ≤ 1), величина реактивной проводимости контура равна:
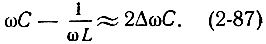
Используя (2-86) и (2-87), выражения (2-78) и (2-83) можно переписать в виде
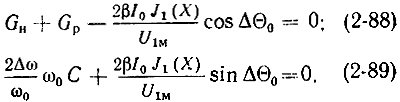
Деля (2-89) на (2-88), получим:
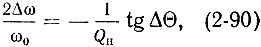
где
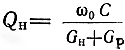
- добротность нагруженного резонатора.
С помощью (2-90), зная параметры резонатора, легко определить изменение частоты в зависимости от изменения угла пролета.
Выражение (2-90) можно записать и в иной форме:
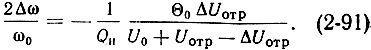
Кривые изменения частоты со в зависимости от -Uотр показаны на рис. 2-28.
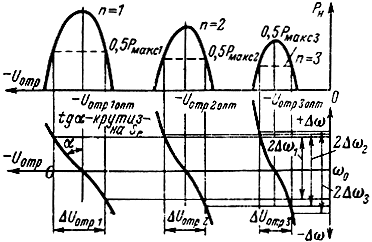
Рис. 2-28. Кривые изменения частоты колебаний и диапазон электронной настройки для различных областей
Диапазон электронной настройки. Пределы электронного управления частотой определяются максимально допустимым отклонением угла пролета от оптимальных значений Θ0 = 2π(n - 1/4). Сгустки электронов должны приходить в резонатор в той части периода колебаний, когда переменное поле обладает достаточным тормозящим действием. В противном случае энергия от электронного потока не передастся полю и колебания сорвутся. Допустимые пределы изменения частоты, называемые диапазоном электронной настройки, принято ограничивать значениями напряжения на отражателе, при которых мощность колебаний уменьшается не более чем в 2 раза по сравнению с ее максимальным значением в центре области (рис. 2-28). При конструировании отражательных клистронов стремятся получить линейную зависимость частоты от напряжения в пределах диапазона 2Δω.
Перепишем (2-89), подставляя туда выражения (2-62) и (2-70):
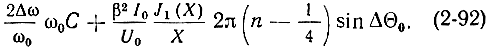
Отсюда видно, что величина диапазона электронной настройки возрастает с увеличением I0, с уменьшением U0 и при переходе к областям колебаний с большими значениями n.
Из выражения (2-90), кроме того, следует, что пределы возможной перестройки частоты расширяются при снижении нагруженной добротности Qн. Уменьшение величины Qн приводит, кроме того, и к повышению линейности кривой Δω = f(Uотр).
В связи с этим для расширения диапазона электронной настройки в клистронах стараются по возможности увеличить I0, снизить ускоряющее напряжение, а также использовать резонаторы с малой емкостью и по возможности малой величиной Qн.
2-13. Параметры и особенности конструкции отражательных клистронов
В качестве параметров отражательных клистронов в справочных данных указываются величины, большинство из которых уже упоминалось выше. Прежде всего это параметры номинального электрического режима: напряжение накала UН, ускоряющее напряжение U0, ток I0, а также пределы изменения напряжения на отражателе Uотр. Поскольку отражательные клистроны обычно используются в качестве маломощных генераторов, величины U0 и Uотр не превышают нескольких сотен вольт.
Основными параметрами также являются: диапазон рабочих волн, выходная мощность Рн, величина которой для большинства приборов составляет сотые или десятые доли ватта, а также диапазон электронной настройки Δω и крутизна электронной настройки, т.е. крутизна кривой ω = f(Uотр).
Обычно Δω ≈ (0,3 ÷ 0,5%) ω0, а значение крутизны измеряется десятыми долями или единицами мгц/в. В специальных клистронах с широким диапазоном электронной настройки величина Δω может достигать 10-15% от значения ω0.
Отражательные клистроны в диапазоне волн от 10 см и длиннее выполняются обычно в стеклянном оформлении. К дисковым выводам от сеток механически крепится внешний металлический объемный резонатор, обычно тороидального типа. Перестройка частоты колебаний осуществляется с помощью специальных плунжеров, вводимых в полость резонатора.
В более коротковолновой части диапазона СВЧ (λ < 10 см) отражательные клистроны имеют металлические баллоны, внутренний объем которых образует резонатор. Перестройка такого резонатора осуществляется прогибом гибкой стенки баллона - диафрагмы, за счет чего меняются расстояния между сетками и, следовательно, емкость резонатора.

© RATELI.RU, 2010-2020
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
