Раздел второй. Квантовые приборы СВЧ и оптического диапазона

Глава седьмая. Физические основы работы квантовых приборов

7-1. Особенности квантовых приборов

Определение. "Квантовыми называют приборы, в которых для различного рода преобразований электромагнитных колебаний используется энергия, связанная с квантовыми переходами частиц, входящих в единый ансамбль (молекула, кристалл твердого тела, газ и др.).

В отличие от электровакуумных электронных приборов, в которых преобразование энергии источника питания в энергию электромагнитных колебаний осуществляется с помощью свободных электронов, движущихся в вакууме, в квантовых приборах для этой цели, как уже было сказано, используются несвободные электроны, входящие в состав того или иного ансамбля частиц.

При изучении физических процессов, лежащих в основе работы электровакуумных приборов - характера движения электронов в вакууме, изменения их энергетического состояния и др. - мы основывались на законах классической механики. Для рассмотрения физических явлений, протекающих в квантовых приборах, законы классической физики непригодны. Движение частиц, их энергетические состояния, процессы взаимодействия друг с другом и с электромагнитным полем подчиняются законам квантовой механики. Поэтому для понимания основных физических процессов, на которых базируется принцип действия квантовых приборов, необходимо знакомство с основными положениями современной квантовой физики.

Терминология квантовых приборов к настоящему времени еще не установилась окончательно, хотя в последние годы ведется серьезная работа по стандартизации терминов квантовой электроники.

Термин квантовые приборы СВЧ, входящий в наименование курса, по программе которого составлен настоящий учебник, недостаточно полно характеризует обширную группу современных квантовых приборов, частотный диапазон работы которых простирается от дециметровых волн до волн длиной в несколько десятых долей микрона (∼ 10^-5 см), соответствующих ультрафиолетовой области оптического диапазона.

Наиболее приемлем для общей характеристики разнообразных приборов этой группы термин квантовые приборы, которым мы и будем пользоваться в дальнейшем.

В отечественной и зарубежной литературе наряду с этим, наиболее общим термином, употребляется и ряд других, подчеркивающих особенность принципа действия или назначения того или иного прибора: атомный генератор, молекулярный генератор, квантовый парамагнитный усилитель, оптический квантовый генератор и др.

Широкое распространение получили также американские термины мазер и лазер, характеризующие соответственно квантовые приборы диапазона СВЧ и оптического диапазона волн. Термины эти являются аббревиатурами английских фраз, кратко характеризующих принцип действия этих приборов: "Microwave (Lightwave) amplification by stimulated emission of radiation".

Начальные буквы слов в этих фразах, означающих в русском переводе "Усиление сверхвысокочастотных колебаний (или световых волн) с помощью вынужденного (индуцированного) излучения", и составили термины мазер и лазер.

Классификация. Установившейся классификации квантовых приборов пока еще не существует, хотя число разработанных приборов, выпускаемых промышленностью и широко используемых в разнообразных областях науки и техники, весьма велико.

Принято, прежде всего, подразделять квантовые приборы по диапазону рабочих частот на две обширные группы: приборы оптического диапазона, включая инфракрасную область - лазеры и приборы сверхвысокочастотного диапазона радиоволн - мазеры.

Второй наиболее употребительный классификационный признак - рабочее вещество. Большую группу образуют газовые квантовые приборы (в основном лазеры), в которых в качестве рабочего вещества используются различные газы или их смеси: Аr; СO₂; He + Ne и др.

Не менее обширна группа квантовых приборов на твердом теле. В этих устройствах используются парамагнитные кристаллы рубина (в квантовых усилителях СВЧ и оптических генераторах); кристаллы CaF₂, BaF₂ с примесью ионов урана U³⁺ и редкоземельных элементов, например самария Sm²⁺, диспрозия Dy²⁺ и др.; ряд других соединений с примесью редкоземельных элементов; стекла с примесями иттербия Yb³⁺; неодима Nd³⁺ и т. п.; а также электронно-дырочные переходы в полупроводниковых соединениях типа A^IIB^VI, A^IIIB^V и др., например ZnS, CdSe, GaAs, InSb и т. д.

Существует группа жидкостных квантовых приборов (лазеров), на основе оксихлорида фосфора и галогенидов металлов либо на основе оксихлорида селена с четыреххлористым оловом. Активным веществом в них является неодим (Nd), растворенный в неорганической жидкости. Созданы также жидкостные лазеры на основе органических красителей.

Наконец, имеется группа квантовых приборов, активным веществом в которых служат атомные или молекулярные пучки - потоки невзаимодействующих между собой атомов или молекул, например атомов цезия (Cs), молекул водорода (Н₂), аммиака (NH₃) и др.

В качестве классификационных признаков используются также: назначение приборов (усилитель, генератор, стандарт частоты, эталон времени и др.), метод создания активного состояния вещества (инверсной населенности), вид колебательной системы или системы охлаждения и др.

Основные свойства. Появление и развитие квантовой электроники - одно из крупнейших, революционных событий в науке и технике последних 10-15 лет.

Из наиболее важных достижений, связанных с возникновением квантовой электроники, следует прежде всего отметить освоение радиоэлектроникой оптического диапазона электромагнитных колебаний. До появления квантовых приборов источниками излучения световых волн служили лампы накаливания, газоразрядные приборы, вольтова дуга и т. п. Излучение этих приборов происходит, как правило, в широком диапазоне частот, с небольшой мощностью и слабой направленностью; колебания немонохроматичны и некогерентны.

С развитием квантовой электроники открылась возможность создания усилителей световых волн, генераторов когерентного света, отличающихся недостижимой ранее стабильностью, мощностью излучения и его направленностью. Так, например, нестабильность квантовых генераторов имеет величину порядка 10^-11 - 10^-12, что на пять-шесть порядков меньше нестабильности кварцевых генераторов. Эта особенность квантовых генераторов используется при создании высокоточных эталонов частоты и времени.

Высокая когерентность излучаемого оптическими квантовыми генераторами света послужила основой для развития нового направления в оптике - голографии, позволяющего получать объемные цветные изображения предметов.

В современных квантовых приборах мощность светового потока достигает в импульсном режиме 10¹¹ вт (в импульсе длительностью 10 пикосекунд при диаметре луча около 1 мм) и в непрерывном режиме - 10⁴ вт. Высокая мощность излучения в сочетании с высокой направленностью (луч лазера может быть сфокусирован на площадке размером 10^-6 см²) открывают богатейшие перспективы использования оптических квантовых приборов для обработки материалов, в медицине, биологии и др.

Важнейшее значение имеет оптический диапазон для радиосвязи, радиолокации, радионавигации и т. п. Информативная емкость этого диапазона электромагнитных колебаний в десятки тысяч раз больше всего радиодиапазона от длинных до сантиметровых волн.

Высокая направленность излучения позволяет во много раз повысить помехоустойчивость радиосистем, разрешающую способность, точность определения координат.

Создание мощных квантовых источников излучения повлекло за собой рождение и развитие новой отрасли физики - нелинейной оптики. При воздействии на вещество мощной световой волны, напряженность электрического поля которой превышает миллионы в/см, нарушаются основные законы линейной оптики: изменяется частота электромагнитных колебаний. Распространение такой волны в среде описывается нелинейными уравнениями. На основе этих явлений возможно, например, создание устройств, позволяющих плавно изменять частоту света, и др.

Важный вклад внесла квантовая электроника и в развитие радиотехники диапазона сверхвысоких частот. Квантовые парамагнитные усилители характеризуются температурой шумов порядка 8-15°К, т. е. обладают в 100 раз большей чувствительностью, нежели обычные радиоприемные устройства этого диапазона. Все перечисленные и некоторые другие достоинства квантовых приборов обусловили чрезвычайно быстрое развитие этой области электроники и широкое внедрение квантовых устройств в самые разнообразные области науки и техники.

7-2. Спонтанное и индуцированное излучение

Энергетическая характеристика атома. Как известно из курса физики, энергия частицы, входящей в некоторый ансамбль, например энергия электрона в атоме, не может принимать произвольные значения. Разрешенные энергетические уровни частицы диктуются законами квантовой механики и определяются набором квантовых чисел, например: главным квантовым числом n, орбитальным квантовым числом l, магнитным орбитальным квантовым числом m_l и магнитным спиновым числом m_s. Возможны и другие сочетания квантовых чисел, которыми мы и будем пользоваться в дальнейшем,, полагая эти сведения хорошо известными читателю из курса физики.

Напомним, что под энергетическим уровнем принято понимать полную энергию частицы в системе, отсчитываемую от некоторого нулевого уровня. Например, для упрощенной модели водородоподобного изолированного атома можно полагать, что электроны связаны с ядром силами кулоновского взаимодействия

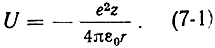
Зависимость U(r) имеет вид гиперболы (рис. 7-1), причем за нулевой уровень принята энергия электрона, удаленного от ядра на бесконечно большое расстояние. Полная энергия электрона в системе равна:

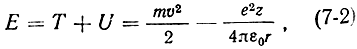
где T = mυ²/2 - кинетическая энергия частицы.

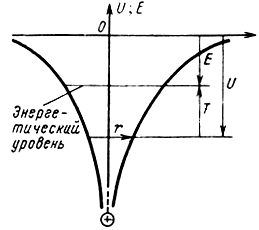
Рис. 7-1. Потенциальная кривая атома

В случае стационарной орбиты сила кулоновского притяжения должна быть уравновешена центростремительной силой

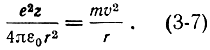
И, следовательно, |Е| = |Т| = |U/2|.

Помимо основного энергетического уровня Е₀, соответствующего наибольшей запасенной энергии, электрон может занимать и ряд уровней возбуждения Е₁, Е₂, Е₃ и т. д. вплоть до нулевого уровня, соответствующего ионизации атома, т. е. отрыва электрона от ядра (рис. 7-2). Совокупность энергетических уровней называется энергетическим спектром атома, молекулы, твердого тела и т. д.

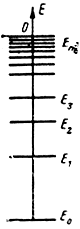
Рис. 7-2. Энергетический спектр атома

Переход электрона с одного (Е_m) разрешенного энергетического уровня на другой уровень (Е_n) сопровождается излучением или поглощением кванта энергии ΔЕ в виде электромагнитных колебаний с частотой

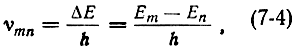
здесь h = 6,62·10^-27 эрг·сек - постоянная Планка.

Переходы с более высокого уровня энергии на более низкий, сопровождающиеся излучением электромагнитных колебаний, называют переходами вниз, а переходы в обратном направлении, при которых система поглощает энергию - переходами вверх.

Разность энергий, соответствующих двум соседним энергетическим уровням, называемая иногда энергетическим зазором, может быть разной по величине. Различны поэтому и частоты излучаемых или поглощаемых электромагнитных колебаний при переходе с одного энергетического уровня на другой. Так, например, из рис. 7-2 видно, что по мере удаления от основного энергетического состояния энергетические зазоры сокращаются.

Величина энергетического зазора однозначно определяет в соответствии с формулой (7-4) частоту излученных или поглощенных электромагнитных колебаний при переходе частицы.

Для изолированных атомов энергетические зазоры достаточно велики. Так, разность энергетических состояний валентных электронов соответствует излучению или поглощению колебаний с частотой, лежащей в диапазоне видимого света. Энергетические зазоры между уровнями электронов внутренних оболочек еще больше; переходы этих электронов сопровождаются рентгеновским излучением.

Энергетический спектр молекул. Широкий диапазон энергетических зазоров наблюдается и в энергетических спектрах молекул, где наряду с энергетическими зазорами, характерными для атомов и соответствующими видимому, ультрафиолетовому и рентгеновскому излучению, наблюдается широкий энергетический спектр, связанный с колебаниями отдельных атомов в молекуле и вращательными движениями атомов и молекулы в целом. Энергетические зазоры между этими уровнями соответствуют частотам инфракрасного излучения и сверхвысоким частотам диапазона радиоволн.

Энергетический спектр ансамбля частиц. Еще богаче энергетический спектр твердого тела, где, как известно, расщепление энергетических уровней отдельных атомов при их объединении в кристалл, приводит к образованию энергетических зон, содержащих большое число дискретных энергетических уровней и разделенных между собой запрещенными зонами - энергетическими промежутками, не содержащими разрешенных энергетических состояний.

В полупроводниках, как известно, ширина запрещенной зоны между зоной проводимости и валентной зоной измеряется десятыми долями или несколькими электронвольтами. Поэтому частоты излученных колебаний при переходе из зоны проводимости в валентную зону должны лежать в длинноволновой части оптического диапазона или в инфракрасной области.

Однако межзонные переходы в полупроводниках не всегда сопровождаются излучением электромагнитной энергии; наблюдаются также безызлучательные переходы, когда энергия рассеивается в кристаллической решетке в виде фононов.

Внесение в химически чистый полупроводник примесей иного вещества обогащает энергетическую диаграмму новыми локальными уровнями примесных атомов, которые могут располагаться в запрещенной зоне. Появляются возможности энергетических переходов между локальными уровнями или обмена частицами между этими уровнями и разрешенными зонами. Подобные переходы используются, в частности, в рубиновом лазере.

Далее при рассмотрении конкретных квантовых приборов мы более подробно остановимся на энергетических характеристиках того или иного вещества, используемого в качестве активной среды. Сейчас же отметим лишь, что практически любой ансамбль частиц, будь то поток невзаимодействующих между собой молекул, газ или твердое тело, характеризуется определенным энергетическим спектром, т. е. набором дискретных энергетических состояний, в которых могут находиться частицы.

Энергетические зазоры между отдельными уровнями могут быть различными по величине, так что переходы частиц вниз с более высоких на более низкие уровни могут сопровождаться излучением с частотами, лежащими в широкой области шкалы электромагнитных колебаний.

Необходимость получения излучения той или иной частоты - в оптическом диапазоне, в инфракрасной области или же в диапазоне сверхвысоких радиочастот - и определяет, главным образом, выбор вещества, на основе которого должен быть создан квантовый прибор.

Нормальное и возбужденное состояние системы. В невозбужденном состоянии электроны в атоме занимают энергетические уровни, соответствующие наименьшей возможной энергии. Такие уровни, как уже говорилось, называют основными. В результате получения некоторой дополнительной энергии извне электрон может перейти на один из уровней возбуждения - уровень, соответствующий более высокой энергии и не занятый другой частицей. Такое возбужденное состояние атома неустойчиво, если только переходы возбужденного электрона вниз на один из свободных энергетических уровней не запрещены квантовыми условиями. Через весьма короткий интервал времени τ возбужденный электрон совершит переход вниз, который будет сопровождаться излучением кванта энергии с частотой υ = ΔE/h, где ΔE - энергетический зазор перехода.

Среднее время жизни. Такой самопроизвольный (спонтанный) переход случаен во времени. Поэтому само событие спонтанного перехода характеризуют некоторой вероятностью A, а время τ пребывания электрона в возбужденном состоянии, которое является среднестатической величиной, называют средним временем жизни электрона в этом состоянии. Вероятность А и среднее время жизни связаны простым соотношением

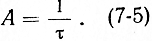
Для большинства случаев величина τ очень мала. Так, для большинства разрешенных оптических переходов τ ≈ 10^-8 сек.

С понятием среднего времени жизни τ тесно связаны такие хорошо известные из физики макросистем понятия, как релаксация и время релаксации. Как известно, в физике релаксацией называется процесс возвращения в состояние термодинамического равновесия макроскопической системы, выведенной из этого состояния у каким-либо внешним воздействием.

Этот процесс, как известно, протекает по экспоненциальному закону. Время, в течение которого разность между возбужденным и равновесным значениями какого-либо параметра системы (например, температуры) уменьшается до величины, равной 1/е от возбужденного значения, называется временем релаксации.

Процесс спонтанного излучения, сопровождающий возвращение Мгновенно возбужденной системы в основное состояние, также протекает по экспоненциальному закону. Для интенсивности спонтанного излучения во времени можно записать:

где I₀ - интенсивность излучения в начале релаксации.

Поэтому среднее время жизни τ в литературе иногда называют временем релаксации.

Метастабильное состояние. В результате возбуждения электрон в атоме может занять такой энергетический уровень, излучательные переходы вниз с которого в данной системе запрещены квантовыми условиями отбора. Такие уровни возбуждения называются метастабильными.

При отсутствии безызлучательных переходов атом в таком состоянии теоретически может находиться бесконечно долго. В реальных системах, однако, атом из такого метастабильного состояния переходит в основное за счет безызлучательных переходов электрона вниз.

Метастабильные уровни играют важную роль в работе некоторых квантовых приборов при накоплении частиц в одном из возбужденных состояний.

Спонтанное излучение. Излучение, сопровождающее спонтанный переход электрона в атоме, называют спонтанным излучением. Если система содержит N атомов, часть из которых по каким-либо причинам оказалась в возбужденном состоянии, то спонтанные переходы будут происходить неодновременно и независимо друг от друга. Поэтому спонтанное излучение отдельных атомов будет случайным не только во времени, но и по основным характеристикам: фазе, поляризации, направлению распространения и др. Таким образом, спонтанное излучение ансамбля атомов подобно флуктуациям электромагнитного поля и, как мы увидим далее, определяет уровень собственных шумов системы.

Индуцированное (вынужденное или стимулированное) излучение и поглощение. Переход электрона с одного энергетического уровня на другой может произойти под воздействием внешнего электромагнитного поля. Переход вниз с более высокого на низший энергетический уровень сопровождается, как обычно, излучением кванта энергии, которое в этом случае называют индуцированным (вынужденным за счет воздействия внешнего электромагнитного поля) излучением. Соответственно переход вверх на более высокий энергетический уровень сопровождается индуцированным поглощением кванта энергии.

Обязательное условие индуцированных переходов - строгое или приближенное равенство кванта энергии внешнего поля разности энергий тех уровней, между которыми совершается переход. Следовательно, частота колебаний индуцирующего (внешнего) излучения должна быть равна частоте индуцированного излучения или поглощения.

Процесс вынужденного излучения или поглощения можно пояснить на модели классического гармонического осциллятора, подвергающегося воздействию внешнего электромагнитного поля, с частотой, равной частоте колебаний осциллятора. Если фазы колебаний волны и осциллятора отличаются на π, то энергия, которой обмениваются волна и осциллятор, отрицательна. Это означает, что энергия осциллятора уменьшается, а энергия волны возрастает. Иначе говоря, в этом случае происходит излучение кванта энергии; частица переходит на нижний энергетический уровень. При этом ни амплитуда, ни фаза, никакой другой параметр возмущающего колебания не меняются. Квант энергии внешнего поля лишь вынуждает, стимулирует переход частицы вниз и сопутствующее ему излучение нового кванта энергии. Излученные, колебания точно совпадают по частоте, фазе, поляризации и направлению распространения с колебаниями, их вызвавшими.

Иными словами, индуцированное излучение когерентно излучению стимулирующему.

В условиях синфазности внешних колебаний и колебаний осциллятора энергия, которой они обмениваются, оказывается положительной. Осциллятор поглощает квант энергии внешнего поля. Иначе говоря, частица, поглотив квант энергии, переходит на более высокий энергетический уровень. Энергия внешнего поля при этом уменьшается на величину поглощенного кванта; наблюдается индуцированное поглощение.

Процессы индуцированного излучения и поглощения могут быть характеризованы определенной степенью вероятности. Интенсивность этих процессов среди ряда факторов зависит и от энергии внешнего индуцирующего поля, точнее от величины плотности его энергии в единичном интервале частот вблизи резонансной частоты (частоты перехода).

Соотношения Эйнштейна. Понятие о спонтанном и индуцированном излучении было впервые введено Эйнштейном при выводе формулы Планка на основании термодинамического рассмотрения взаимодействия вещества с полем.

Пусть имеется некоторая система частиц, характеризуемая лишь двумя энергетическими состояниями Е₁ и Е₂ (Е₂ > Е₁) и находящаяся в термодинамическом равновесии. Число частиц, находящихся в состоянии Е₁, обозначим через N₁ а число частиц в состоянии Е₂ - через N₂. Для определения числа частиц на том или ином уровне Эйнштейн пользовался статистикой Больцмана, согласно которой вероятное число частиц с энергией Е_n определяется выражением

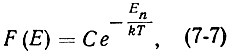
здесь

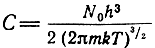
постоянная величина; N₀ - концентрация частиц.

Как известно, квантовые ансамбли подчиняются законам квантовой статистики Ферми - Дирака или Бозе - Эйнштейна. Однако в случае невырожденного электронного газа функция распределения Ферми - Дирака частиц по энергетическим состояниям переходит в больцмановскую функцию F(Е).

Таким образом, в рассматриваемой системе вероятное число частиц на уровне с энергией Е₂ равно:

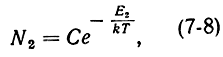
а на уровне с энергией Е₁

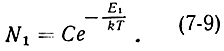
В системе возможны переходы частиц вниз с уровня Е₂ на уровень E₁ (переход 2 → 1), а также вверх, с уровня Е₁ на уровень Е₂ (переход 1 → 2).

Запишем для вероятности спонтанного перехода 2 → 1 одной частицы за время dt следующее выражение:

где A₂₁ - коэффициент спонтанного излучения, характеризующий вероятность перехода частиц с уровня 2 на уровень 1.

Пусть система подвергается воздействию внешнего излучения с частотой υ₂₁, равной частоте перехода 2 → 1, и плотностью энергии u_υ в единичном интервале частот вблизи резонансной частоты υ₂₁. Под воздействием этого излучения возможны переходы вниз (2 → 1) и вверх (1 → 2), сопровождающиеся соответственно индуцированным излучением и индуцированным поглощением.

Вероятности этих переходов для одной частицы за интервал времени dt равны:

где величины В₂₁ и В₁₂ - коэффициенты индуцированного излучения и поглощения, характеризующие вероятности соответствующих переходов.

Вероятности переходов в системе, естественно, зависят от числа частиц, населяющих уровни Е₁ и Е₂. Так, например, вероятность спонтанного перехода 2 → 1 тем выше, чем больше частиц на уровне Е₂. Следовательно, вероятность спонтанных переходов в системе

Для индуцированных переходов

и

Если система находится в равновесии, то вероятности переходов в единицу времени вверх и вниз должны быть равны. В противном случае наблюдался бы непрерывный рост числа частиц на одном из уровней (заселение уровня частицами) и уменьшение частиц на другом уровне (обеднение уровня частицами). Таким образом, для условия равновесия можно записать:

Или, учитывая (7-8) и (7-9):

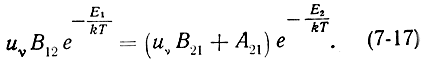
На основании соображений, приведенных выше, можно заключить, что

В самом деле, при облучении системы внешним электромагнитным полем вероятности процессов индуцированного поглощения или излучения зависят от фазовых соотношений между колебаниями элементарного осциллятора и возбуждающей волны. В любой момент времени фазы этих колебаний случайны, и поэтому вероятности случаев синфазности и противофазности должны быть равны.

Проводя изложенное выше рассмотрение, Эйнштейн постулировал, что излучение, поглощаемое и испускаемое частицами системы, находящейся в термодинамическом равновесии, должна удовлетворять известной формуле Планка:

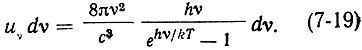
На основании выражения (7-17) с учетом (7-18) можно записать:

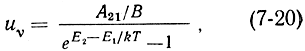
где В = В₁₂ = В₂₁.

Сопоставляя это выражение с (7-19), легко видеть, что оно совпадает с формулой Планка при условиях:

и

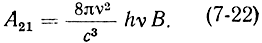
Выражение (7-22), связывающее коэффициенты спонтанных и индуцированных переходов, играет важную роль в квантовой электронике. Напомним, что величина 8πυ²/c³ в формуле Планка характеризует число типов колебаний в единице объема и в единичном интервале частот для объема, линейные размеры которого велики по сравнению с длиной волны λ = c/υ. С помощью формулы (7-22) можно установить соотношение между уровнем полезного индуцированного излучения, характеризуемого коэффициентом В, и уровнем спонтанного излучения (коэффициент А₂₁), определяющего собственные шумы системы. Так, например, для частоты υ = 10 Ггц подстановка численных значений в (7-22) дает: А₂₁ ≈ 6 · 10^-28 В. Следовательно, в области сверхвысоких частот индуцированное излучение значительно превосходит спонтанное, даже в том случае если u_υ невелико.

Из (7-22) видно также, что спонтанное излучение, определяющее уровень собственных шумов системы, растет пропорционально υ³ и зависит от параметров колебательной системы: числа возможных типов волн, полосы пропускания и др.

7-3. Инверсная населенность

Отвлечемся пока что от спонтанного излучения, считая его достаточно малым, и рассмотрим условия, при которых в системе частиц, облученной внешним электромагнитным полем, возможно преобладание индуцированного излучения. Пусть по-прежнему система характеризуется двумя энергетическими состояниями Е₁ и Е₂ (E₂ < E₁) и числом частиц на этих уровнях N₁ и N₂ соответственно. Частота колебаний внешнего излучения равна

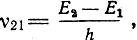
а плотность энергии u_υ.

Частицы в системе, находящейся в нормальном состоянии, распределяются по энергетическим уровням в соответствии с функцией распределения (7-7) статистики Больцмана (рис. 7-3). Более высокий энергетический уровень заселен меньшим числом частиц (N₂ < N₁). При повышении температуры функция F(Е) становится положе, но условие N₂ < N₁ выполняется при любой конечной температуре.

Вероятности индуцированных переходов в системе вверх и вниз определяются соотношениями (7-14) и (7-15). При условии, что B₂₁ = B₁₂ = B и N₂ < N₁, P'₂₁ < Р'₁₂. В системе преобладают индуцированные переходы вверх. Система частиц поглощает энергию внешнего электромагнитного поля. С подобными явлениями мы часто сталкиваемся в жизни: радиоволны затухают при распространении в атмосфере земли, интенсивность световых волн падает при их прохождении через различные среды и т. д.

Очевидно, что в рассматриваемой системе частиц будет преобладать индуцированное излучение лишь в том случае, если вероятность переходов вниз будет больше вероятности переходов вверх (P'₂₁ > Р'₁₂). Это возможно лишь при условии что на верхнем энергетическом уровне будет больше частиц, чем на нижнем: N₂ > N₁. Состояние вещества или системы, в которой выполняется это условие, называется состоянием с инверсией (обращением) населенности уровней. Или, просто говорят, что в системе наблюдается инверсная населенность уровней. Вещество с инверсной населенностью называют также активным веществом.

Отрицательная температура. Иногда в литературе инверсную населенность характеризуют отрицательной температурой. Этот термин можно объяснить следующим образом. В соответствии с законом распределения статистики Больцмана для отношения числа частиц на двух уровнях (7-8) и (7-9) можно записать:

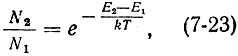
отсюда

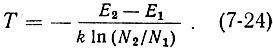
Если N₂ < N₁, то T > 0. При любой конечной положительной температуре на нижнем энергетическом уровне находится большее число частиц. Частицы в системе стремятся занять состояния с меньшей энергией. С повышением температуры экспонента на рис. 7-3 становится более пологой, но в любом случае выполняется неравенство N₂ < N₁.

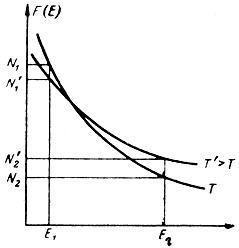
Рис. 7-3. Кривые распределения частиц по энергетическим состояниям

Температура становится отрицательной только при условии N₂ > N₁, что соответствует инверсной населенности уровней. Чем сильней неравенство N₂ > N₁, тем более "отрицательна" температура.

Следует иметь в виду, что температура Т, о которой идет речь, не является абсолютной температурой вещества, ибо отрицательная абсолютная температура с физической точки зрения не имеет смысла. Температура Т в (7-24) - это некоторая условная величина - температура квантового перехода, используемая в квантовой электронике для характеристики отношения населенностей уровней.

При равенстве населенностей уровней (N₁ = N₂) температура Т = ∞. Система находится в состоянии насыщения; она прозрачна для внешнего излучения, так как число переходов вниз в среднем равно числу переходов вверх.

Вполне понятно, что из этих трех возможных состояний (Т < 0; T > 0 и Т = ∞) устойчивым является лишь одно, отвечающее положительной температуре. В одно из двух других - возбужденных - состояний система может быть переведена при затрате некоторой внешней энергии и лишь при определенных условиях.

В квантовых приборах в качестве активных подбираются такие вещества, в которых индуцированные переходы вниз сопровождались бы излучением электромагнитной энергии с нужной частотой. Задача получения и поддержания в течение нужного времени активного состояния вещества, т. е. состояния с инверсной населенностью - одна из важнейших задач квантовой электроники.

Число активных частиц. Систему с инверсной населенностью характеризуют также числом активных частиц

где N_m - число частиц на уровне с энергией Е_m, a N_n - число частиц на уровне Е_n, причем Е_m > Е_n.

Коэффициент инверсии. Другой величиной, характеризующей степень инверсии населенностей, является коэффициент инверсии

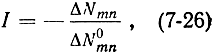
здесь ΔN_mn - количество активных частиц в инверсном состоянии системы, а ΔN⁰_mn - разность населенностей уровней Е_m и Е_n при термодинамическом равновесии. Поскольку в этих условиях N_m < N_n, то величина ΔN⁰_mn отрицательна.

7-4. Методы создания инверсной населенности

В настоящее время в квантовой электронике разработан и успешно используется ряд методов создания в системе частиц инверсной населенности. Как правило, рациональность того или иного метода определяется физическими характеристиками самой системы, используемой в качестве активного вещества в квантовом приборе.

Напомним, что, как отмечалось выше, квантовые приборы, помимо деления их на устройства оптического и сверхвысокочастотного диапазонов, различают также по физическим параметрам активного вещества: газовые квантовые приборы; приборы на атомных и молекулярных пучках; квантовые приборы на твердом теле и др. Для каждой из этих групп разработаны особые методы инвертирования населенностей, связанные с особенностями .квантовых физических процессов, лежащих в основе принципа действия этих приборов. Однако известны и более общие методы, как, например, метод энергетической накачки, применяемый как для газовых, так и для приборов на твердом теле.

Далее, при рассмотрении конкретных квантовых приборов мы, по возможности подробно, остановимся на физических явлениях, протекающих в некоторых наиболее употребительных в квантовой электронике активных веществах. Это позволит также оценить и обосновать используемые для различных активных веществ методы создания инверсной населенности. Сейчас же попытаемся лишь дать краткую характеристику основных методов возбуждения вещества в рамках, необходимых для дальнейшего изложения.

Метод сортировки частиц. Этот метод, используемый в некоторых квантовых приборах, работающих на атомных или молекулярных пучках, заключается в пространственном разделении рабочих частиц, находящихся в различных энергетических состояниях. На пути атомов или молекул, движущихся от источника частиц к рабочему объему, располагается сортирующее устройство, проходя которое частицы меняют траекторию своего движения (рис. 7-4).

Рис. 7-4. Метод сортировки частиц

Частицы с более высокой энергией отклоняются к оси и через входную диафрагму попадают в рабочий объем. Частицы же с меньшей энергией, наоборот, отклоняются от оси и большинство их не проходит через диафрагму. Таким образом, в рабочий объем попадают преимущественно частицы с более высокой энергией, образуя систему с инверсивной населенностью уровней.

В качестве сортирующих используются устройства, создающие постоянное во времени, но неоднородное в поперечном сечении электрическое или магнитное поле. Неоднородное электрическое поле Воспользуется для сортировки частиц, обладающих свойствами электрических диполей, а неоднородное магнитное поле - для разделения частиц с отличным от нуля магнитным моментом.

Сортировка частиц квадрупольным конденсатором. Примером сортирующего устройства с неоднородным электрическим полем может служить квадрупольный конденсатор - устройство, состоящее из 4, 6, 8 и т. д. стержневых электродов, половина которых подключена к положительному полюсу источника постоянного напряжения, а другая половина - к отрицательному (рис. 7-5, а). Электрическое поле равно нулю вблизи оси такого конденсатора и увеличивается по мере удаления от оси и сокращения расстояния между стержнями.

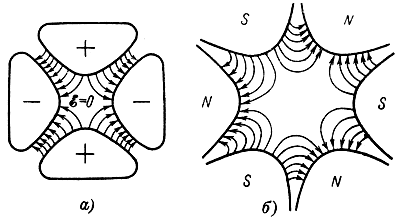
Рис. 7-5. Электрический квадрупольный (а) и магнитный (б) конденсаторы

Молекулы некоторых веществ в силу неравномерного относительно центра масс распределения электронов обладают собственным электрическим дипольным моментом р. В других молекулах такой дипольный момент может быть индуцирован электрическим полем за счет смещения электронных оболочек. В любом случае частица, обладающая электрическим дипольным моментом, произвольно ориентированным относительно вектора ε напряженности поля, будет испытывать со стороны этого поля вращающее возмущение до тех пор, пока диполь не окажется параллельным или антипараллельным силовым линиям поля. В первом случае, при параллельной ориентации, энергия взаимодействия между диполем и полем минимальна и равна U_мин = -рε. Во втором случае энергия взаимодействия максимальна: U_макс = pε. Если электрическое поле однородно, то оба эти положения устойчивые. В неоднородном электрическом поле на диполь, параллельно ориентированный вектору ε, будут действовать силы смещения до тех пор, пока он не переместится в область с наибольшей напряженностью поля и энергия взаимодействия не окажется минимально возможной. Диполь, ориентированный антипараллельно, будет в неоднородном электрическом поле смещаться по той же причине в область с наименьшей напряженностью поля.

Таким образом, в электрическом поле происходит изменение энергетического состояния частицы. Это явление, как известно из курса физики, называется эффектом Штарка. Изменение энергетического состояния частицы может проявляться в виде смещения энергетического уровня Е на величину ΔE в том случае, если уровень Е невырожден. Для вырожденного уровня энергии наблюдается его расщепление на несколько уровней, число которых равно степени вырождения. Величина штарковского расцепления ΔЕ, т. е. величина энергетического зазора между расщепленными уровнями зависит от величины напряженности поля и может изменяться с ростом ε по линейному (линейный эффект Штарка) либо по квадратичному (квадратичный эффект Штарка) закону.

Таким образом, частицы, попадая в неоднородное электрическое поле, например такое, как в квадрупольном конденсаторе (рис. 7-5, а), изменяют траекторию движения: молекулы с меньшей энергией отклоняются в область максимальной напряженности поля, т. е. к периферии, а молекулы, обладающие более высокой энергией, фокусируются вблизи оси конденсатора. По выходе из сортирующего устройства в рабочий объем попадают, как уже было сказано, преимущественно частицы с большей энергией.

Подобным же образом с помощью магнитного конденсатора (рис. 7-5, б) может быть осуществлено пространственное разделение частиц, обладающих собственным магнитным моментом μ. Энергия взаимодействия таких частиц с магнитным полем U = |μ|В. Вследствие эффекта Зеемана энергетические уровни в магнитном поле также расщепляются на ряд уровней, число которых равно степени вырождения.

Метод энергетической накачки. Энергетической накачкой в квантовой электронике называют процесс нарушения равновесного распределения частиц по энергетическим состояниям под воздействием внешнего электромагнитного излучения. Метод энергетической накачки применяется для систем частиц, обладающих тремя и более энергетическими уровнями. В двухуровневой системе создать инверсную населенность частиц с помощью внешнего электромагнитного излучения нельзя.

Насыщение перехода. Рассмотрим уже знакомую нам систему частиц с двумя энергетическими состояниями Е₁ и Е₂ (E₂ > E₁). В состоянии термодинамического равновесия распределение частиц по энергетическим уровням подчиняется законам статистики Больцмана. При любой конечной температуре N₂ < N₁. Предположим, что система подвергается внешнему облучению с частотой υ₁₂ = (Е₂ - E₁)/h. Под действием этого излучения возникают индуцированные переходы вверх (1 → 2) и вниз (2 → 1). Вероятности этих переходов в единицу времени равны P'₁₂ = u_υ B₁₂ N₁ и Р'₂₁ = u_υ B₁₂ N₂ соответственно, причем Р'₁₂ > Р'₂₁, так как N₁ > N₂. Taким образом, происходит постепенное заселение энергетического уровня Е₂ за счет преимущественных индуцированных переходов частиц вверх. По мере заселения уровня Е₂ разность N₁ - N₂ становится все меньше и в пределе уменьшается до нуля. Населенности уровней Е₁ и Е₂ выравниваются. При этом, естественно, становятся равными вероятности переходов: P'₁₂ = P'₂₁.

Система становится прозрачной для частоты ν₁₂, так как интенсивности индуцированного излучения и поглощения равны. Такое состояние называют насыщением перехода.

В реальных условиях система стремится за счет спонтанных и релаксационных переходов возвратиться из состояния насыщения в состояние, соответствующее термодинамическому равновесию. При достаточной плотности внешнего излучения u_ν эти процессы могут быть скомпенсированы. Таким образом, насыщение перехода наблюдается в условиях некоторого поглощения электромагнитной энергии.

Трехуровневая система. Рассмотрим теперь систему частиц с тремя уровнями энергии Е₁, Е₂ и Е₃ (Е₁ < Е₂ < Е₃), которые населены частицами в условиях термодинамического равновесия в соответствии с законом классической статистики Больцмана (экспонента на рис. 7-6, а и б). Предположим, что к системе подводится внешнее излучение с частотой ν₁₃ = (E₃ - E₁)/h. Под воздействием этого излучения наблюдаются преимущественные индуцированные переходы вверх (1 → 3), так как N₁ > N₃. Уровень Е₃ заселяется до тех пор, пока не наступит насыщение перехода и населенности уровней Е₁ и Е₃ окажутся равными (N'₁ = N'₃).

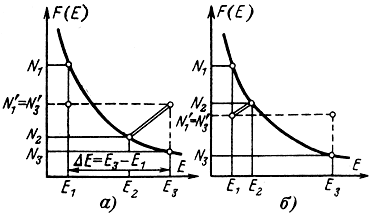
Рис. 7-6. Получение инверсной населенности в трехуровневой системе. а - на переходе 3 → 2; б - на переходе 2 → 1

Пренебрежем пока релаксационными и спонтанными переходами.

Из сравнения рис. 7-6, а и б видно, что в первом случае (E₃ - E₂ < E₂ - E₁) инверсия населенностей образуется в системе уровней Е₃ и Е₂: населенность N'₃ уровня Е₃ в состоянии насыщения выше населенности уровня Е₂. Во втором случае (Е₃ - Е₂ > Е₂ - Е₁) картина иная: инвертированными оказываются населенности уровней Е₂ и Е₁ (N₂ > N'₁).

Следовательно, в первом случае преимущественное индуцированное излучение может быть получено на переходе 3 → 2 с частотой ν₃₂ = (Е₃ - E₂)/h, а во втором случае - на переходе 2 → 1 с частотой ν₂₁ = (E₂ - E₁)/h. Переходы между уровнями с инверсной населенностью называют рабочими переходами.

Таким образом, в трехуровневой системе под воздействием энергетической накачки может быть получена инверсная населенность, причем накачка должна происходить с частотой, соответствующей энергетическому зазору между крайними уровнями. Излишне, по-видимому, доказывать невозможность инвертирования системы за счет облучения с частотой ν₁₂ и ν₂₃. Инверсия населенностей получается между средним уровнем и одним из крайних: заселяемым или опустошаемым в зависимости от соотношения между энергетическими зазорами, на которых не происходит накачка.

Связь между частотой накачки и рабочей частотой. Соотношение между энергетическими зазорами в системе играет важную роль, ибо энергетические уровни могут оказаться расположенными так, что в состоянии насыщения N'₁ = N'₃ = N₂ (рис. 7-7) и инверсии населенностей не получится.

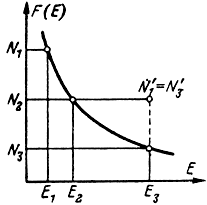
Рис. 7-7. Расположение трех уровней, при котором инверсия населенностей не достигается

Кроме того, между частотой накачки и частотой, соответствующей рабочему переходу, должно быть определенное соотношение.

Выразим населенности N₂ и N₃ уровней Е₂ и Е₃ в состоянии термодинамического равновесия через населенность N₁

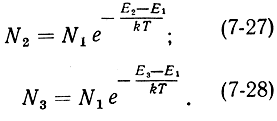
Обычно в квантовых приборах величины энергетических зазоров между рабочими уровнями много меньше средней тепловой энергии частиц

Поэтому экспоненты в (7-27) и (7-28) можно разложить в ряд и ограничиться первым членом ряда

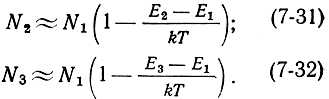
В состоянии насыщения перехода 1 → 3 под действием накачки населенности уровней Е₁ и Е₃ равны: N'₁ = N'₃. Следовательно, с учетом (7-32) можно записать:

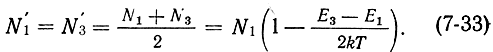
Если рабочим является переход 2 → 1, то N₂ > N'₁. Учитывая (7-31) и (7-33), запишем:

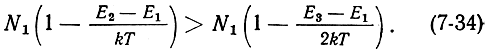
Откуда следует:

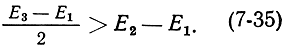
Зазору Е₃ - Е₁ соответствует частота накачки ν₃₁, а рабочему зазору Е₂ - Е₁ - рабочая частота индуцированного излучения V2i. Следовательно, на основании (7-35)

Иначе говоря, частота накачки ν_н должна более чем вдвое превышать частоту полезного сигнала ν_c, т. е. частоту индуцированного излучения на рабочем переходе

Влияние релаксационных процессов. В проведенные рассуждения существенную поправку могут внести релаксационные процессы в системе. Предположим, что в рассматриваемой системе протекают интенсивные релаксационные процессы между уровнями Е₃ и Е₂. Время жизни τ₃ частиц на уровне Е₃ невелико, a время жизни частиц на уровне Е₂ больше: τ₂ > τ₃. Тогда по мере переходов частиц с уровня Е₁ на уровень Е₃ под действием накачки с частотой ν₃₁ уровень Е₂ будет заселяться интенсивней, чем уровень Е₃ (рис. 7-8). При достаточно сильном неравенстве τ₂ > τ₃ это явление будет наблюдаться независимо от соотношения энергетических зазоров Е₃ - Е₂ и Е₂ - Е₁. Рабочим переходом в этом случае будет переход Е₂ → Е₁.

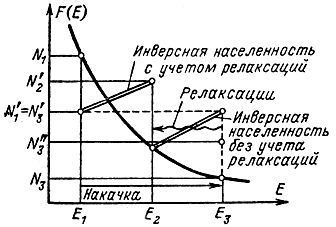
Рис. 7-8. Влияние релаксаций на процесс создания инверсной населенности

Аналогичным образом, инверсная населенность может быть получена на переходе Е₃ → Е₂, если между уровнями Е₂ и Е₁ протекают интенсивные релаксационные процессы.

В квантовой электронике условия инверсии с учетом интенсивности релаксационных процессов определяют, решая кинетические уравнения системы, описывающие с помощью коэффициентов W_mn вероятности релаксационных переходов, скорости изменения числа частиц на энергетических уровнях. Решение этих уравнений позволяет определить в условиях насыщения перехода 1 → 3 и с учетом релаксационных процессов такие величины, как населенности уровней и число активных частиц:

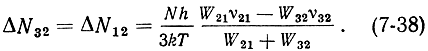
Здесь ΔN₃₂ = N'₃ - N₂; ΔN₁₂ = N'₁ - N₂; N = N₁ + N₂ + N₃ - полное число частиц, a W₂₁ и W₃₂ - вероятности релаксационных переходов 2 → 1 и 3 → 2 соответственно.

Из (7-38) видно, что для получения инверсии населенностей на переходе 3 → 2(N'₃ > N₂ и ΔN₁₂ > 0) необходимо, чтобы выполнялось неравенство W₂₁ν₂₁ > W₃₂ν₃₂.

Иначе говоря, необходимо, чтобы уровень Е₂ был бы расположен ближе к уровню Е₃, чем к уровню E₁(ΔE₂₁ > ΔE₃₂ и ν21 > ν₃₂), и чтобы релаксационные переходы протекали наиболее интенсивно на переходе 2 → 1 (W₂₁ > W₃₂), опустошая нижний уровень Е₂ рабочего перехода. Из условия ν₂₁ > ν₃₂, в частности, следует, что частота накачки ν₃₁ должна быть более чем вдвое выше частоты сигнала ν₃₂, так как ν₃₁ = ν₂₁ + ν₃₂.

Аналогичным образом можно сформулировать условия для получения инверсной населенности на переходе 2 → 1.

Инверсия населенностей в четырехуровневой системе. Использование четырех энергетических уровней позволяет при определенных условиях получать большую инверсию, чем в трехуровневой системе, снижать частоту накачки до величины, превышающей частоту сигнала, а не удвоенную частоту, как это требовалось в трехуровневой системе, и кроме того, в некоторых случаях получить инверсную населенность для перехода с частотой сигнала, превышающей частоту накачки (ν_c > ν_н).

На рис. 7-9 показаны некоторые случаи получения инверсной населенности в четырехуровневой системе. В отличие от предыдущих графиков N = f(E), которые были использованы для иллюстрации населенностей энергетических уровней, здесь изображены одномерные энергетические диаграммы, где по оси ординат отложена энергия. Такими, более простыми диаграммами, принятыми в литературе по квантовой электронике, мы и будем пользоваться в дальнейшем, показывая условно стрелочками различные виды переходов: релаксационные, рабочие, под воздействием накачки и др.

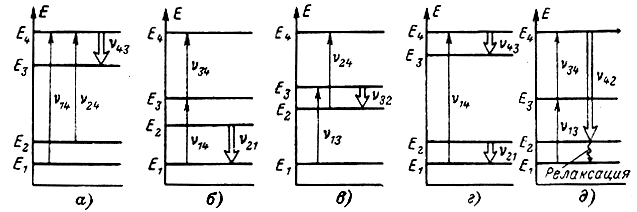
Рис. 7-9. Возможные варианты использования четырехуровневой системы

В системе, представленной на рис. 7-9, а накачка осуществляется на двух частотах ν₁₄ и ν₂₄. При этом верхний уровень Е₄ рабочего перехода 4 → 3 обогащается одновременно частицами с первого и второго уровней и инверсия рабочего перехода существенно увеличивается.

На рис. 7-9, б показана так называемая сдвоенная накачка, когда сигналом одной частоты ν₁₄ = ν₃₄ одновременно насыщаются два перехода. При этом интенсивно обедняется частицами нижний уровень E₁ рабочего перехода 2 → 1. Сдвоенная накачка эквивалентна насыщению одного перехода в трехуровневой системе с удвоенной частотой накачки.

В системе на рис. 7-9, в равны энергетические зазоры ΔE₁₃ и ΔE₂₄. Накачкой с частотой ν₁₃ = ν₂₄ одновременно обогащается верхний уровень Е₃ и обедняется нижний уровень Е₂ рабочего перехода 3 → 2. При этом методе необходимо соблюдение условия ν_н > ν_c, a не ν_н > 2ν_c, как это требуется в трехуровневой системе.

В случае, показанном на рис. 7-9, г, используются два одинаковых рабочих перехода: ν₂₁ = ν₄₃. Сигнал накачки с частотой ν₁₄ одновременно обедняет нижний уровень Е₁ рабочего перехода 2 → 1 и обогащает верхний уровень E₄ второго рабочего перехода 4 → 3. Число активных частиц при этом получается в 1,5 раза больше, нежели в трехуровневой системе.

На рис. 7-9, д показан один из возможных случаев, когда ν_c > ν_н. Накачка с частотой ν₁₃ = ν₃₄ интенсивно обогащает верхний уровень Е₄ рабочего перехода 4 → 2. Получение инверсной населенности обусловлено преобладанием вероятности W₂₁ релаксационных переходов над всеми остальными релаксационными вероятностями.

Метод энергетической накачки используется во многих квантовых приборах: газовых, полупроводниковых, твердотельных, парамагнитных и др. Частота накачки выбирается в зависимости от энергетической характеристики активного вещества. Во многих случаях частота лежит в оптическом диапазоне и поэтому вместо термина энергетическая накачка в этих случаях применяют термин оптическая накачка.

Методы получения инверсной населенности в газовых квантовых приборах. Помимо метода энергетической накачки, применяемого, например, для возбуждения газового лазера на парах цезия, в газовых приборах используются методы создания инверсной населенности, специфические лишь для приборов этого класса.

Наиболее распространен метод инвертирования населенностей за счет столкновений атомов или молекул газа со свободными электронами, быстро движущимися в электрическом поле. Эти явления хорошо известны как из курса физики, так и из курса "Электронные приборы", в котором достаточно подробно обсуждались физические процессы электрического разряда в газе. За счет столкновений быстролетящих электронов с атомами или молекулами газа в баллоне с достаточно низким давлением (от 10^-2 до единиц мм рт. ст.) происходят процессы объемной ионизации частиц или их возбуждения. В последнем случае электроны в атомах или молекулах газа, получив дополнительную энергию, переходят на более высокие энергетические уровни - уровни возбуждения. Последующие спонтанные переходы возбужденных частиц в основное состояние сопровождаются излучением (свечение газа в тиратронах с неоновым наполнением, стабилитронах, газосветых рекламных лампах и т. п.).

В газовых квантовых приборах избыток возбужденных атомов или молекул образует инверсную населенность, которая и используется затем для получения индуцированного излучения.

Второй метод также основан на процессах возбуждения частиц газа, но используется для этой цели не энергия быстролетящих свободных электронов, а энергия неупругих атомных столкновений.

Для перевода атомов и молекул газа в возбужденные состояния может быть использован также и высокочастотный электрический разряд в газе, который возникает при помещении баллона с разреженным газом в сильное высокочастотное электрическое поле.

Метод диссоциации молекул используется в тех приборах, где рабочим веществом служит совокупность молекул. Диссоциация (распад) молекулы на составные части: атомы или радикалы может произойти либо в результате ее столкновения с атомом, либо под воздействием интенсивного светового потока (фотодиссоциация), либо в результате взрыва и т. п.

При диссоциации молекулы продукты распада оказываются в возбужденном состоянии. Так, например, при облучении световой вспышкой молекула CF₃J распадается на радикал CF₃ и атомарный иод J, который оказывается в возбужденном состоянии. При интенсивном процессе такого рода фотодиссоциации создается инверсия населенностей уровней атомов иода.

Поскольку процессы диссоциации сопровождаются разрывом химической связи, такие приборы часто называют химическими квантовыми приборами (химический лазер).

Методы получения инверсной населенности в твердотельных квантовых приборах. В большинстве квантовых приборов с активным веществом в виде твердого тела инверсия населенностей достигается методами энергетической накачки. Этот принцип используется в лазерах на рубине и на других кристаллах с примесями редкоземельных элементов, а также в парамагнитных квантовых усилителях.

7-5. Принцип работы квантовых приборов

Квантовое усиление. Предположим, что некоторое вещество, в энергетическом спектре которого имеются уровни энергии Е₁ и Е₂ (E₂ > E₁), облучается потоком электромагнитной энергии со спектральной плотностью u_ν (рис. 7-10). Положим также, что вещество активно, т. е. с помощью какого-либо метода на переходе 2 → 1 получена инверсная населенность (N₂ > N₁) с числом активных частиц ΔN = N₂ - N₁. Пусть, кроме того, частота падающего излучения

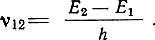
В этом случае под воздействием падающего излучения наблюдается преимущественное индуцированное излучение. Если по мере распространения электромагнитной энергии вдоль оси z в некотором элементарном слое dz индуцируется в результате перехода вниз один новый квант энергии с частотой ν₁₂, то в следующем слое два кванта индуцируют еще два новых кванта и т. д. В веществе развивается лавинное размножение квантов с частотой ν₁₂, при котором в каждой элементарной области вещества скорость нарастания электромагнитной энергии пропорциональна самой энергии. Иными словами, интенсивность электромагнитной волны нарастает с координатой z по экспоненциальному закону

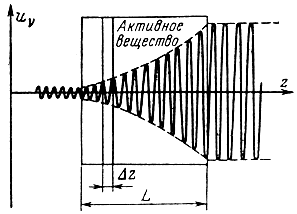
Рис. 7-10. Квантовое усиление колебаний

В соответствии с (7-39) интенсивность электромагнитной энергии на пути z = 1/χ возрастает в е раз, а по выходе из вещества достигнет величины u⁰_ν e^χL.

Величина χ, имеющая размерность [см^-1], называется коэффициентом квантового усиления. Его величина пропорциональна вероятности Р'₂₁ индуцированных переходов 2 → 1, числу активных частиц и величине кванта hν₁₂

В случае, если вещество не активно, т. е. населенности уровней подчиняются законам статистики Больцмана (в частности, N₁ > N₂), наблюдается преимущественное индуцированное поглощение. Интенсивность падающего излучения уменьшается с координатой z по экспоненциальному закону

В реальных устройствах всегда протекают процессы, приводящие к потерям электромагнитной энергии (рассеяние при взаимодействии с решеткой в твердом теле, излучение по другим направлениям и др.). Поэтому в соотношение (7-39) необходимо ввести коэффициент потерь

Причины, определяющие величину β, специфичны для каждого типа рабочего вещества.

Из (7-42) следует, что для получения эффекта квантового усиления необходимо, чтобы χ > β. Удовлетворить это неравенство далеко не просто, так как коэффициент к в реальных условиях относительно невелик. Так, например, для рубина χ ≈ 10^-2 см^-1 и для получения усиления порядка 10² потребовались бы размеры активного вещества около 5 м. Поэтому в квантовых приборах для сокращения длины взаимодействия активное вещество помещают в резонатор, настроенный на частоту индуцированного излучения.

Принцип работы квантового усилителя. На рис. 7-11 показана схема, поясняющая принцип работы квантового усилителя. Активное вещество, в энергетическом спектре которого содержатся три необходимых энергетических уровня Е₁, Е₂ и Е₃ (Е₁ < Е₂ < Е₃), помещено в объемный резонатор. В качестве рабочего используется переход 3 → 2.

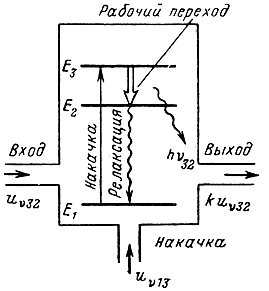
Рис. 7-11. К принципу работы квантового усилителя

Размеры объемного резонатора выбраны такими, что его резонансная частота ν₀ равна частоте излучения на рабочем переходе: ν₀ = ν₃₂. Через один из фидеров к активному веществу подводится сигнал энергетической накачки с частотой ν₁₃. Практическую сторону осуществления энергетической накачки мы рассмотрим позже.

Под воздействием излучения с частотой ν₁₃ вещество становится активным: частицы с уровня Е₁ переходят на уровень E₃. Предположим, что спектральная плотность сигнала накачки u_ν13 достаточно велика для того, чтобы создать инверсию населенностей на переходе 3 → 2.

Если через входную линию подвести к резонатору колебания, подлежащие усилению с частотой ν₃₂, то в резонаторе, настроенном на эту частоту, в результате многократного отражения волны от его стенок установится стоячая волна. Под воздействием этого электромагнитного поля в рабочем веществе возникнет и будет развиваться процесс индуцированного излучения. Кванты энергии, излученной при индуцированных переходах частиц с уровня E₃ на уровень Е₂, когерентные с возбуждающим полем, поддерживают колебания, возникшие в резонаторе. Иными словами, энергия электромагнитных колебаний в резонаторе непрерывно пополняется за счет индуцированного излучения.

Рассматриваемая система, как и любая другая, не свободна от потерь. Часть электромагнитной энергии через выходную линию отводится в нагрузку; определенная доля энергии теряется в самом резонаторе и в активном веществе. Поэтому режим работы системы зависит от соотношения между энергией E_изл, поступающей в резонатор за счет индуцированного излучения, и суммарной энергией потерь Е_п. Если E_изл + E_с:вх < E_п, то подводимая ко входу энергия сигнала E_с.вх поглощается системой, амплитуда колебаний на выходе меньше амплитуды колебаний на входе: E_с.вых < E_с.вх.

Если же энергия E_изл + E_с.вх превышает потери в резонаторе и активном веществе, но меньше суммарной энергии Е_п потерь, включающей отвод энергии в нагрузку, то система работает как усилитель. Амплитуда колебаний в выходной линии больше амплитуды колебаний, подводимых ко входу: E_с.вых > E_с.вх.

Таким образом, система представляет собой усилитель с положительной обратной связью, обеспечиваемой резонатором, в который помещено активное вещество. Необходимые фазовые условия выполняются за счет преимущественного заселения верхнего энергетического уровня рабочего перехода. Увеличение энергии сигнала обусловлено преобладающим индуцированным излучением - размножением квантов энергии в активном веществе, когерентных входному сигналу. Энергетические соотношения в системе таковы, что энергия индуцированного излучения, обеспечивая режим квантового усиления, недостаточна, однако, для поддержания режима самовозбуждения.

Режим самовозбуждения. Если E_изл > E_п, то система перейдет в режим самовозбуждения и превратится в генератор. В этом случае колебания в системе будут существовать даже при отсутствии сигнала на входе.

Для поддержания колебаний стационарной амплитуды должны быть выполнены определенные условия, необходимые для сохранения неравенства E_изл > Е_п. Иначе говоря, в рассматриваемой системе, как и в любом автогенераторе, должен выполняться баланс мощностей. Энергия E_изл, получаемая за счет индуцированного излучения, должна быть достаточной для восполнения как потерь в самом генераторе, так и части энергии, отводимой в нагрузку.

Величина энергии E_изл пропорциональна числу ΔN активных частиц. По мере осуществления индуцированных переходов 3 → 2 верхний энергетический уровень E₃ рабочего перехода опустошается, а уровень Е₂ заселяется частицами. Для поддержания нужной величины ΔN плотность энергии накачки должна быть достаточной для обеспечения необходимой скорости заселения уровня Е₃ частицами с уровня Е₁. Кроме того, необходима определенная скорость опустошения уровня Е₂ за счет релаксационных переходов 2 → 1. Все эти процессы в режиме стационарной амплитуды колебаний должны находиться в динамическом равновесии.

Итак, в рассмотренной системе активное вещество все время находится в электромагнитном поле стоячей волны в резонаторе. Электромагнитная волна при многократных отражениях от стенок резонатора как бы много раз проходит через активное вещество.

Резонаторные системы используются в квантовых приборах любого диапазона волн. В усилителях и генераторах СВЧ колебаний в качестве колебательных систем используются, как правило, объемные резонаторы или замедляющие системы, уже знакомые нам по электронным СВЧ приборам.

В оптическом диапазоне устройство резонаторов иное. Обычно это система зеркал, многократно отражающих световые лучи. Более подробно оптические резонаторы мы рассмотрим при изучении квантовых приборов оптического диапазона (гл. 9).

7-6. Характеристики излучения

Особенности физических процессов в квантовых приборах послужили причиной введения ряда характеристик квантового излучения электромагнитных колебаний. Особенно эти характеристики важны для приборов, работающих в оптическом диапазоне волн.

Ширина спектральной линии. До сих пор мы рассматривали энергетический спектр некоторого ансамбля частиц как совокупность дискретных, бесконечно "узких" энергетических уровней. Квантовые переходы между такими энергетическими уровнями должны сопровождаться излучением или поглощением электромагнитных колебаний со строго определенной частотой ν = ΔE/h, определяемой величиной энергетического зазора ΔЕ. Иначе говоря, излучение или поглощение, сопровождающее квантовый переход, рассматривалось как строго монохроматическое. В действительности, конечно, строго монохроматическое колебание, определяемое как гармонический процесс, длящийся бесконечно долго, не может быть получено. Излучение или поглощение электромагнитных волн, связанное с квантовым переходом в реальных системах, характеризуется определенным спектром частот, который в квантовой электронике, как и в спектроскопии, называется шириной спектральной линии (рис. 7-12). Спектр квантового излучения или поглощения, в простейшем случае двух дискретных энергетических уровней, по форме подобен резонансной кривой колебательного контура. Это и понятно, так как частица, как известно, может быть представлена в виде элементарного гармонического осциллятора. На рис. 7-12 по оси абсцисс отложена частота, а по оси ординат - интенсивность излучения I. Ширина спектральной линии Δν_л определяется по уровню, соответствующему 0,5 максимальной интенсивности излучения на резонансной частоте.

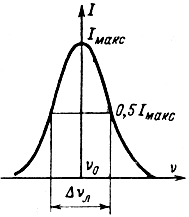
Рис. 7-12. Ширина спектральной линии

Конечная ширина спектральной линии объясняется целым рядом причин, часть которых связана с особенностями той или иной системы частиц. Однако в любом случае величина Δν_л0 не может быть равна нулю.

Естественная ширина спектральной линии. Даже в идеальном случае двух дискретных энергетических уровней частицы, не подвергающейся никакому воздействию внешних факторов, ширина спектральной линии конечна. Величина Δν_л0, называемая в этом случае естественной шириной спектральной линии, определяется уширением дискретных энергетических уровней в соответствии с соотношением неопределенностей Гейзенберга

Отсюда следует, что ΔЕ → 0 в том случае, если время жизни Δτ частицы в данном энергетическом состоянии бесконечно велико (Δτ → ∞). В действительности время жизни Δτ всегда конечно и, следовательно, конечна ширина ΔЕ энергетического уровня, а значит конечна и естественная ширина спектральной линии Δν_л0. Так, например, естественная ширина спектральной линии молекулы аммиака (NH₃), квантовый переход которой с частотой 23870 Мгц использовался в одном из первых квантовых генераторов, равна примерно 10^-3 гц. В других случаях величина Δν_л0 может быть еще больше. В оптическом диапазоне, например, вследствие уменьшения Δτ с возрастанием энергетического зазора в рабочем переходе относительная величина Δν_л0 существенно увеличивается.

В реальных ансамблях частиц (газах, жидкостях, твердых телах) на величину ширины спектральной линии оказывают влияние и другие факторы.

Причины уширения спектральных линий. Одна из возможных причин увеличения ширины спектральных линий атомов или молекул газа - это эффект Доплера. В результате хаотического движения частиц газа их скорости относительно неподвижного приемничка излучения оказываются различными. Различны поэтому и величины доплеровского смещения частоты для каждого из такой совокупности хаотически движущихся элементарных осцилляторов. Ширина спектра частот с учетом доплеровского эффекта пропорциональна средневероятной тепловой скорости частицы (и поэтому зависит от температуры), а также частоте квантового перехода. Наибольшее уширение спектральных линий в результате эффекта Доплера наблюдается поэтому в оптическом диапазоне. Но и в области сверхвысоких частот доплеровское уширение значительно превосходит естественную ширину спектральной линии. Так, для молекул аммиака при комнатной температуре (Т ≈ 300°К) доплеровское ширение Δν_D ≈ 70 кгц.

В газовых ансамблях, используемых в квантовых приборах в качестве активного вещества, уширение спектральных линий происходит также из-за столкновений частиц между собой и со стенками сосуда. При неупругих соударениях изменяется энергетическое состояние частицы и, следовательно, сокращается ее время жизни Δτ на данном энергетическом уровне, что и приводит в соответствии с (7-43) к уширению линии. Уширение спектральной линии за счет соударений частиц пропорционально среднему времени свободного пробега частицы и поэтому существенно зависит от давления газа в сосуде. Для газообразного аммиака, находящегося под давлением в несколько десятых долей миллиметров ртутного столба уширение линии может достигать десятка мегагерц.

Увеличение ширины спектральной линии происходит также вследствие воздействия электрического и магнитного полей.

Излучение квантовых генераторов оптического диапазона происходит, как правило, в полосе частот, значительно меньшей ширины спектральной линии, и определяется, в основном, полосой пропускания оптического резонатора и условиями квантового усиления.

Более подробно этот вопрос рассматривается в гл. 9.

Обычно степень монохроматичности излучения оценивается специальным коэффициентом

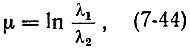
где λ₁ и λ₂ - длины волн, соответствующие границам спектра излучения.

Когерентность. Как известно из физики и курса "Радиотехнические цепи и сигналы", под когерентностью понимают согласованность фаз колебаний в различных точках пространства в некоторый заданный момент времени или же в различные моменты времени, но в одной заданной точке. Соответственно различают пространственную когерентность и временную когерентность. Первое понятие используется как характеристика когерентных свойств волны в направлении, перпендикулярном направлению ее распространения. Часть пространства, занятого волной, в котором выполняются условия когерентности, называют объемом когерентности.

Понятие временной когерентности связано со степенью монохроматичности волны. Монохроматические колебания одной частоты всегда когерентны. Два колебания считают когерентными, если за время τ - интервал когерентности - их разность фаз остается неизменной или изменяется в допустимых пределах.

В квантовых приборах индуцированное излучение всегда когерентно с излучением стимулирующим.

Луч оптического квантового генератора когерентен по всему поперечному сечению. Объем когерентности лазерного луча очень велик.