
Глава восьмая. Квантовые приборы сверхвысоких частот
8-1. Особенности квантовых приборов СВЧ
Для получения эффекта квантового усиления или генерации колебаний сверхвысоких частот необходимо использование в качестве активной среды таких веществ, энергетический спектр которых содержал бы энергетические зазоры в пределах примерно от 0,4·10-5 до 1,2·10-3 эв, что соответствует длинам волн от 30 см до 1 мм. Необходимо также, чтобы квантовые переходы между нужной парой энергетических уровней были бы разрешенными.
Интенсивные исследования энергетических спектров широкого круга веществ в твердом, газообразном и жидком состоянии, проводившиеся за последние два десятилетия, показали, что этим требованиям удовлетворяют многие элементы и соединения. В частности, в первом квантовом генераторе, созданном в 1954-1955 гг., в качестве активного вещества были использованы молекулы аммиака (NH3). Этот молекулярный квантовый генератор работал в диапазоне СВЧ на частоте 23870 Мгц.
В дальнейшем в квантовой электронике диапазона сверхвысоких частот преимущественное использование нашли твердые кристаллические вещества, обладающие парамагнитными свойствами. К таким веществам принадлежит обширная группа соединений, содержащих парамагнитные ионы - ионы с некомпенсированными электронными спинами, например ионы элементов группы железа, ионы группы палладия и др.
В настоящее время в диапазоне СВЧ используются, главным образом, квантовые парамагнитные усилители, обладающие по сравнению с усилителями на электронных СВЧ приборах рядом преимуществ. Основное достоинство квантовых усилителей - низкий уровень собственных шумов, величина которого в лучших образцах имеет порядок 8-15°К, т. е. примерно в 100 раз ниже уровня шумов наиболее чувствительных усилителей на электронных СВЧ приборах. Следует отметить, что указанная величина шумовой температуры определяется, главным образом, шумами антенны и подводящих фидеров. Собственные шумы квантового усилителя, основным источником которых является спонтанное излучение, характеризуются шумовой температурой порядка 0,5-5°К. Столь низкий уровень собственных шумов достигается в квантовых усилителях ценой значительных конструктивных усложнений: активное вещество помещается в криостат - специальное охлаждающее устройство, содержащее жидкий гелий и жидкий азот. Поэтому конструктивно квантовый усилитель получается достаточно громоздким и малопригодным для использования в радиосистемах на подвижных объектах.
По другим параметрам - динамическому диапазону, ширине полосы пропускания и др. - квантовые усилители обычно уступают усилителям сверхвысокочастотных колебаний других типов.
Тем не менее, в силу высокой чувствительности квантовые усилители нашли широкое применение в стационарных системах сверхдальней радиолокации, радиоастрономии, дальней космической связи и др.
Квантовые генераторы колебаний диапазона сверхвысоких частот до сих пор не получили применения в практике. Преимущество в этой области остается за электронными приборами СВЧ, способными обеспечить значительно более высокий уровень мощности генерируемых колебаний и к. п. д., обладающими возможностью электронного управления частотой и отличающимися относительной конструктивной простотой.
8-2. Квантовый генератор на молекулах аммиака
Устройство молекулярного квантового генератора на пучке молекул аммиака (NH3) схематически показано на рис. 8-1.
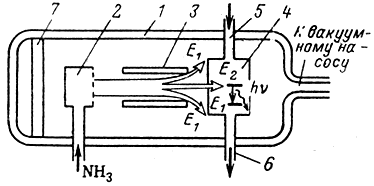
Рис. 8-1. Устройство квантового генератора (усилителя) на молекулах аммиака. 1 - кожух; 2 - испаритель; 3 - квадрупольный конденсатор; 4 - резонатор; 5 - входная линия; 6 - выходная линия; 7 - сосуд с жидким азотом
В специально охлаждаемый кожух помещено устройство испарения аммиака, поступающего из внешнего резервуара. Молекулы газообразного аммиака через отверстия в стенке испаряющей камеры выходят в рабочее пространство, в котором создается вакуум порядка 10-5 мм рт. ст. Далее частицы попадают в сортирующее устройство - квадрупольный конденсатор, выходе которого молекулы, находящиеся в более высоком энергетическом состоянии Е2, поступают через диафрагму в объемный резонатор. Молекулы с более низкой энергией Е1 не попадают в резонатор и затем частично откачиваются из рабочего пространства насосом, а частично вымерзают на стенках сосуда, содержащего жидкий азот, температура которого равна 77°К (температура замерзания аммиака 195°К).
Объемный резонатор настроен на частоту квантового перехода ν12 = (E2 - E1)/h. В режиме установившихся колебаний электромагнитное поле резонатора индуцирует переходы молекул аммиака с энергетического уровня Е2 на уровень Е1. Энергия индуцированного излучения частично расходуется на восполнение потерь в самой системе, а частично через волновод отводится в нагрузку.
Энергетический спектр молекулы аммиака. Молекула аммиака имеет вид тетраэдра - правильной пирамиды (рис. 8-2), основанием которой служит равносторонний треугольников вершинах которого располагаются атомы водорода. Атом азота размещается в вершине пирамиды на расстоянии h ≈ 0,37 Аº от плоскости основания.
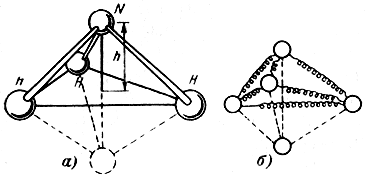
Рис. 8-2. Модель молекулы аммиака (а) и ее механическая аналогия (б)
В общем случае, полная энергия молекулы слагается из энергии ее поступательного движения, колебательной энергии, ротационной энергии - энергии вращательного движения вокруг некоторой оси и, наконец, энергии, характеризуемой взаимодействием между вращательным и колебательным движениями.
В молекулярном генераторе используются энергетические уровни, связанные с колебательным движением, точнее с колебаниями атома азота вдоль оси симметрии z молекулы, совпадающей с высотой h тетраэдра (рис. 8-2, а).
Эти колебания - ангармонические, т. е. периодические, но не синусоидальные - часто называют инверсионными колебаниями, так как в результате такого движения положение атома азота инвертируется относительно основания пирамиды - плоскости, содержащей атомы водорода. Атом азота оказывается то ниже, то выше основания пирамиды, причем крайние положения атома N являются устойчивыми и соответствуют минимумам потенциальной энергии системы (рис. 8-3). Ход кривой U(z) легко объяснить, представив молекулу NH3 механической моделью (рис. 8-2, б) в виде такой же пирамиды, образованной четырьмя шариками, связанными между собой пружинами. Верхнее и нижнее положения шарика в вершине пирамиды устойчивы: силы притяжения и рассталкивания, действующие между шариками, уравновешены. В процессе "продавливания" шарика из верхнего положения в нижнее приходится преодолевать силу сопротивления пружин, часть которых (связывающих атомы водорода) работает при этом на растяжение, а другая часть - на сжатие. Наибольшая энергия системы отвечает положению всех четырех шариков в плоскости основания пирамиды.
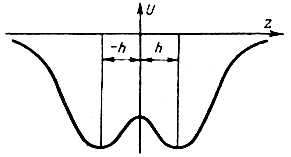
Рис. 8-3. Потенциальная функция молекулы аммиака
Таким образом, два устойчивых состояния атома азота на расстояниях z = ±h от плоскости атомов водорода разделены потенциальным барьером шириной порядка 0,7 Аº и высотой около 0,25 эв.
Если предположить атомы водорода неподвижными, то в каждом из двух устойчивых состояний атом азота, а с ним и вся молекула будет описываться своей волновой функцией. Иначе говоря, атом азота в каждой из двух потенциальных ям можно представить некоторым гармоническим осциллятором. Ввиду достаточно узкого потенциального барьера, разделяющего две потенциальные ямы, вероятность обнаружения частицы за барьером имеет конечную величину. Образуется система из двух гармонических осцилляторов, связанных между собой, причем волновые функции могут образовать как симметричную, так и несимметричную комбинации. Двум этим случаям соответствует дублет - два различных энергетических состояния Е1 и E2, разделенных, как показывают вычисления и эксперимент, энергетическим промежутком ΔЕ12 величиной порядка 10-4 эв.
Эти два энергетических состояния соответствуют двум противоположно ориентированным электрическим дипольным моментам молекулы. Вследствие различия электронных оболочек атомов азота и водорода "центр" суммарного отрицательного заряда электронов в молекуле не совпадает с "центром" суммарного положительного заряда ядер. Это обстоятельство и объясняет наличие в молекуле NH3 электрического дипольного момента, ориентация которого в пространстве меняется на противоположную при инверсии атома азота, осциллирующего относительно плоскости с инверсионной частотой ν12 = ΔE12/h.
В системе молекул NH3, находящейся в термодинамическом равновесии, распределение частиц по энергетическим состояниям E1 и Е2 подчиняется законам статистики Больцмана. В верхнем энергетическом состоянии Е2 находится меньше частиц, чем в нижнем.
Образование пучка молекул. Для уменьшения ширины линии индуцированного излучения необходимо сформировать пучок невзаимодействующих между собой молекул. В противном случае в результате взаимодействия частиц между собой спектральная линия будет уширена и стабильность частоты излучения ухудшится. С этой целью решетка, через которую молекулы NH3 выходят из испарителя в рабочее пространство, должна иметь строго определенные размеры отверстий и расстояний между ними. Величина отверстий не должна превышать среднюю длину свободного пробега молекул в испарителе. По этой же причине не может быть повышено сверх определенной величины и давление газа в испарителе. При нарушении этих условий вблизи отверстий будут наблюдаться соударения молекул и условие их невзаимодействия будет нарушено.
Сортировка молекул. По выходе из испарителя большая часть молекул попадает в неоднородное поле квадрупольного конденсатора, устройство и конфигурация электрического поля в котором были рассмотрены в гл. 7.
В неоднородном электрическом поле конденсатора молекула- диполь с параллельной ориентацией относительно вектора ε - испытывает действие электрических сил, смещающих ее в область максимальной напряженности поля, где энергия Uвз минимальна. Это означает, что молекулы NH3, дипольный момент которых параллелен полю ε и которые, следовательно, находятся на нижнем энергетическом уровне Е1, будут по мере прохождения квадрупольного конденсатора перемещаться от его оси к периферии. По выходе из конденсатора большая часть таких молекул не попадает в резонатор (рис. 8-1).
Противоположное смещение - от стержней к оси конденсатора - получают молекулы, находящиеся на верхнем энергетическом уровне Е2. Их дипольный момент антипараллелен полю, и энергия взаимодействия минимальна в области с наименьшей напряженностью поля, т. е. у оси конденсатора. Большая часть этих молекул проникает через диафрагму в объемный резонатор. Следовательно, в резонатор после сортирующего устройства попадает пучок молекул NH3, подавляющая часть которых находится в верхнем энергетическом состоянии Е2.
Режим усиления. Колебания сверхвысокой частоты u = UM sin ω0t, подлежащие усилению, подводятся к резонатору, настроенному на частоту ω0 = 2πν21, где ν21 - частота квантового перехода Е2 → Е1. Под действием электромагнитной волны в резонаторе индуцируются квантовые переходы E2 → E1 и Е1 → Е2 молекул аммиака. Поскольку число N2 молекул в верхнем энергетическом состоянии больше числа N1 - молекул с энергией Е1, индуцированное излучение преобладает над индуцированным поглощением.
Поле излученных молекулами квантов, будучи когерентно с индуцирующим переходы полем, суммируется с ним, и усиленные колебания через выходной волновод отводятся в нагрузку.
Коэффициент усиления и полоса пропускания молекулярного усилителя являются функцией добротности объемного резонатора с учетом связи его с входным и выходным волноводами, а также способности активного вещества излучать и рассеивать энергию электромагнитных колебаний под действием поля в резонаторе. Последняя величина зависит от целого ряда факторов: конфигурации резонатора и вида колебаний, возбуждаемых в нем, длины пути молекул в резонаторе, скорости их движения и др. Естественная ширина спектральной линии молекулы .аммиака очень мала, и ширина полосы пропускания усилителя определяется временем τ пребывания молекулы в электромагнитном поле резонатора. Эта величина при обычной длине резонатора l ≈ 10 см и средней скорости движения молекул υ‾ ≈ 105 см/сек составляет примерно 0,1 мсек, что соответствует полосе пропускания Δν = 1/τ ≈ 10 кгц.
Уровень собственных шумов молекулярного усилителя, как и других квантовых усилителей, определяется, в основном, двумя факторами: спонтанным излучением активного вещества и тепловым излучением устройств, окружающих активное вещество - стенок резонатора, волноводов и др. Уровень шумов, обусловленных спонтанным излучением в усилителе на молекулах аммиака пренебрежимо мал, так как вероятность спонтанных переходов за время τ пролета молекулы через резонатор стремится к нулю. Невелик также и уровень тепловых шумов при рабочей температуре жидкого азота, равной 77°К.
Поскольку квантовый прибор на пучке молекул NH3 не находит практического применения в качестве усилителя СВЧ колебаний, все вопросы, связанные с источниками шумов и методами их оценки, мы рассмотрим далее на примере других квантовых усилителей СВЧ.
Режим генерации. Выше, в гл. 7, уже отмечалось, что объемный резонатор позволяет не только увеличить время взаимодействия электромагнитного поля с активным веществом, но и обеспечивает положительную обратную связь в приборе.
С увеличением плотности потока молекул NH3, поступающих в резонатор, и ростом индуцированного излучения квантовый усилитель может перейти в режим самовозбуждения и превратиться в генератор. Как и для любого автогенератора, условия самовозбуждения определяются балансом мощностей и балансом фаз. Последнее условие обеспечивается в рассматриваемом квантовом приборе преобладанием в объемном резонаторе молекул с более высоким уровнем энергии. Что же касается баланса мощностей, то это условие будет выполнено в том случае, если энергия индуцированного излучения будет превосходить энергию, отводимую в нагрузку, и энергию потерь в самом устройстве. Так, например, при указанной выше длине резонатора l ≈ 10 см и средней скорости молекул υ‾ ≈ 105 см/сек условие баланса мощностей будет выполнено, если среднее значение потока молекул, поступающих в резонатор, будет не менее 1014 частиц в секунду.
Квантовый генератор на пучке молекул аммиака отличается высокой стабильностью частоты генерируемых колебаний и поэтому может быть использован как высокоточный стандарт частоты. Нестабильность частоты зависит от ряда факторов: расстройки резонатора, изменения величины напряжения на сортирующем конденсаторе и др. Однако влияние этих факторов относительно невелико. Так, например, при расстройке объемного резонатора на 10 кгц уход частоты генератора составит всего лишь 10 гц.
При величине излучаемой мощности порядка 10-10 вт нестабильность молекулярного генератора, т. е. отношение средней величины отклонения частоты Δω к рабочей частоте ω0 составляет величину порядка 10-11.
8-3. Электронный парамагнитный резонанс
Парамагнитные вещества. Как известно из курса физики, парамагнитными называют такие вещества, в которых под действием внешнего магнитного поля индуцируется магнитный момент, совпадающий по направлению с внешним полем. Иначе говоря, восприимчивость парамагнетиков положительна и обычно увеличивается с понижением температуры.
Парамагнитными свойствами могут обладать свободные электроны в полупроводниках и металлах, центры окрашивания, примесные атомы, а также атомы и ионы, обладающие отличным от нуля собственным магнитным моментом.
В квантовой электронике используются кристаллические вещества, парамагнетизм которых обусловлен примесными ионами элементов, принадлежащих переходным группам в периодической системе. Это - группа железа (элементы с 21-го по 30-й), группа палладия (39-48-й элементы), группа редких земель (57-70-й), группа платины (71-80-й) и группа актинидов (89-100-й элемент). Наибольшее применение находят элементы групп железа и редких земель. Парамагнитные свойства атомов этих веществ определяются нескомпенсированными спинами электронов внутренних электронных оболочек: 3dn электронами в группе железа и 4fn электронами в группе редких земель. Атомы большинства таких элементов в химических соединениях превращаются в парамагнитные ионы, т. е. сохраняют парамагнитные свойства в отличие, например, от атомов щелочноземельных элементов, парамагнитные свойства которых, обусловленные нескомпенсированными спинами валентных электронов, теряются при химических соединениях. Так, например, парамагнетизм железа 1s22s22p63s23p63d64s2 с электронной конфигурацией обусловлен электронами незаполненной 3d оболочки. В соединениях железа валентные связи обеспечиваются двумя 4s и одним 3d электронами и атом превращается в парамагнитный ион Fe3+.
Атом в магнитном поле. Если атом, обладающий магнитным моментом M‾J, поместить в постоянное магнитное поле, то на него будет действовать вращающий момент, пропорциональный величине магнитного момента M‾J, индукции магнитного поля B‾ и углу в между M‾J и направлением вектора В‾. Под влиянием этих сил момент M‾J будет прецессировать вокруг вектора B‾ с ларморовой частотой
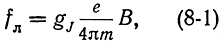
величина которой не зависит от угла Θ. Здесь gJ - фактор Ланде.
Положение M‾J во внешнем магнитном поле, как и любого другого магнитного момента, пространственно квантовано. Его проекция на направление z магнитного поля должна быть кратна целому или полуцелому числу h/2π
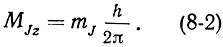
Магнитное квантовое число mJ может принимать 2J + 1 значений: mJ = J; J-1; ... 0 ... -J, где J - полное квантовое число атома. Примеры возможных ориентации момента M‾J показаны на рис. 8-4.
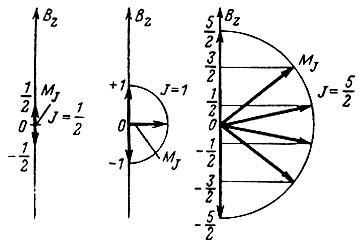
Рис. 8-4. Возможные ориентации полного момента в магнитном поле при различных значениях J
Ориентационная энергия, запасаемая атомом с магнитным моментом M‾J в постоянном магнитном поле, равна:
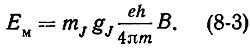
Таким образом, в зависимости от ориентации момента M‾J относительно вектора В‾ появляются 2J + 1 новых энергетических состояний. Иначе говоря, внешнее магнитное поле снимает вырождение уровня J с кратностью вырождения в отсутствии поля, равной 2J + 1.
Расщепление энергетического состояния атома в магнитном поле, как известно, называется зеемановским расщеплением, а получившиеся новые энергетические подуровни - зеемановскими энергетическими уровнями.
Как следует из (8-3), величина расщепления энергетических состояний прямо пропорциональна индукции В магнитного поля (рис. 8-5).
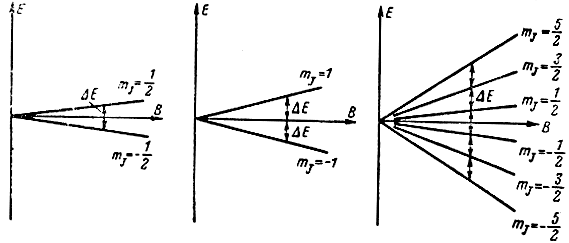
Рис. 8-5. Расщепление энергетических состояний в магнитном поле
В соответствии с квантовыми законами разрешены такие изменения энергетических состояний, при которых число mJ изменяется на единицу. Таким образом, разрешенные изменения ΔE энергии равны:
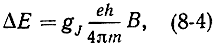
а соответствующая частота перехода
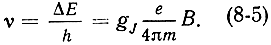
Во многих случаях gJ ≈ 2 и выражение (8-5) принимает удобный для практического использования вид:
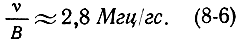
В классическом опыте Зееманом были обнаружены переходы между подуровнями, образовавшимися в результате расщепления различных уровней - состояний, соответствующих различным значениям J. Переходы между такими подуровнями, разделенными относительно большими энергетическими зазорами, сопровождаются в большинстве случаев излучением в оптическом диапазоне.
Явления парамагнитного резонанса, обнаруженные спустя почти 50 лет, связаны с переходами между энергетическими подуровнями, принадлежащими одному и тому же уровню, т. е. состоянию с определенным значением J. Частоты этих переходов, как правило, лежат в диапазоне сверхвысоких частот, и поэтому наблюдение явлений парамагнитного резонанса оказалось возможным лишь в результате развития техники СВЧ.
Явление парамагнитного резонанса. Электронным парамагнитным резонансом (ЭПР) называют явление поглощения или излучения электромагнитной энергии парамагнитным веществом, помещенным в постоянное магнитное поле. Пусть парамагнитный атом, обладающий моментом М‾J, помещен в постоянное поле В‾0 (рис. 8-6).
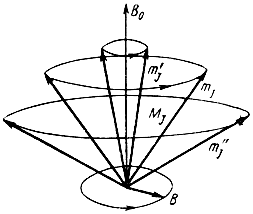
Рис. 8-6. К пояснению явления парамагнитного резонанса
В соответствии с правилами пространственного квантования угол α между вектором В‾0 и образующей конуса, по поверхности которого процессирует вектор момента М‾J, определяется одним из возможных значений квантового числа mJ. Внешнее электромагнитное поле имеет круговую поляризацию и ориентировано так, что вектор В магнитной индукции вращается в плоскости, перпендикулярной В‾0. Результирующее магнитное поле в каждый момент времени определяется геометрической суммой векторов В‾0 и В. Если направление вращения вектора В‾ противоположно направлению прецессии момента М‾J, то в среднем эффект воздействия поля В‾ будет равен нулю. Такой же результат получится в случае совпадения направлений вращения векторов М‾J и В‾, но при отличии частоты f электромагнитных колебаний от частоты прецессии fл.
Иной эффект наблюдается при совпадении направлений вращения и частот (f = fл). Суммарный вектор магнитной индукции, отклоняясь от направления В‾0, будет прецессировать вокруг этого направления с частотой f. В результате появится постоянно действующий на вектор М‾J опрокидывающий момент. Действие этого момента приводит к возникновению дополнительных колебаний, налагающихся на прецессию вектора М‾J. В зависимости от разности фаз электромагнитных колебаний и прецессионного движения вектор М‾J может занять одно из ближайших разрешенных состояний, соответствующих квантовым числам m'J или m''J. При этом энергия атома в суммарном магнитном поле соответственно увеличится или уменьшится. Поскольку все фазовые соотношения равновероятны, то одинаково вероятны для отдельного атома оба этих перехода. В любой системе в соответствии с законами статистики в более низком энергетическом состоянии находится большее число атомов. Поэтому и число возможных переходов вверх, в состояние с большей энергией будет больше числа переходов вниз. В итоге при облучении помещенного в постоянное магнитное поле парамагнитного вещества электромагнитной энергией с частотой f = fл будет наблюдаться поглощение этой энергии - парамагнитный резонанс.
Парамагнитный резонанс в твердых телах. В сложных системах взаимосвязанных атомов или молекул, например в твердых телах, описанные выше для изолированного атома явления существенно усложняются,
Во-первых, в подавляющем большинстве атомов не наблюдается в чистом виде нормальная LS-связь, при которой электростатическое взаимодействие между электронами преобладает над магнитным спин-орбитальным взаимодействием. В некоторых случаях наблюдается иной вид связи, когда преобладающим оказывается взаимодействие между спиновым и орбитальным моментами каждого электрона.
Во-вторых, атомы в кристалле подвергаются воздействию внутренних магнитного и электрического полей. Так, например, в кристалле, содержащем парамагнитные ионы, на каждый ион действует магнитное поле соседних ионов, величина которого может достигать сотни гаусс. Вследствие тепловых колебаний узлов решетки это поле флуктуирует и, следовательно, ионы находятся под действием случайным образом меняющегося магнитного поля. Следует, правда, отметить, что в квантовых приборах обычно используются так называемые разбавленные парамагнитные соли - кристаллы немагнитных веществ с добавлением (0,01-1)% парамагнитных ионов. Примером такого кристалла может служить широко применяемый в квантовой электронике рубин - окись алюминия Аl2O3, в которой часть ионов Аl3+ замещена парамагнитными ионами Сr3+. В таких разбавленных кристаллах действие магнитных полей соседних ионов, естественно, ослаблено.
В любом кристалле, однако, существует довольно сильное внутрикристаллическое электрическое поле, направление и величина которого различны для разных кристаллографических направлений. Под действием этого поля энергетические уровни атомов претерпевают штарковское расщепление. Так, обычно под влиянием внутрикристаллического поля энергетические уровни атомов и ионов с нечетным числом электронов и в особенности низший нормальный уровень расщепляются на два подуровня.
В результате всех упомянутых выше факторов в кристаллах наблюдается сложная структура атомных энергетических уровней, которая уже не может быть описана квантовыми числами L, S и J.
Так, например, согласно экспериментальным данным для многих кристаллов наблюдается подавление орбитального момента атома M‾L и величина полного момента M‾J определяется, в основном, спиновым моментом M‾S. Иначе говоря, магнитные свойства атома в твердом теле определяются его спиновым моментом. Поэтому часто в литературе, рассматривая магнитные кристаллы, говорят о системе спинов, т. е. о системе спиновых моментов, определяющих магнитные свойства вещества.
Во внешнем магнитном поле атомные энергетические уровни кристалла претерпевают зеемановское расщепление, в большинстве случаев анизотропное и не описываемое квантовыми числами mJ. Характер и величина расщепления энергетических уровней, как правило, различны для различных углов между какой-либо кристаллографической осью и направлением внешнего магнитного поля.
На рис. 8-7 показана для примера картина расщепления энергетических уровней фторсиликата никеля (NiSiF6) во внешнем магнитном поле.
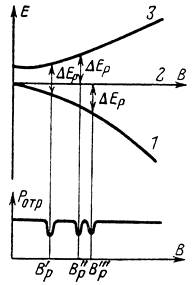
Рис. 8-7. Спектр парамагнитного резонанса фторсиликата никеля
Спектр парамагнитного резонанса. Если такой кристалл облучать электромагнитной волной с частотой νp = ΔEp/h, плавно изменяя при этом напряженность внешнего постоянного магнитного поля, то при определенных значениях В'p, В"p и В"'p,соответствующих переходам с частотой νp, будет наблюдаться парамагнитный резонанс. В зависимости Pотр = f(B) - отраженной от кристалла электромагнитной волны - появляются провалы, регистрирующие поглощение электромагнитной волны кристаллом. Ряд значений В, соответствующих парамагнитному резонансу при заданной величине νp, или, наоборот, значения ν при некоторой величине B = const называют спектром парамагнитного резонанса для данного вещества.
Ширина линии. Поглощение энергии при парамагнитном резонансе наблюдается в пределах некоторого диапазона частот вблизи центральной частоты резонанса. Этот диапазон частот Δνл, как уже упоминалось в гл. 7, называется шириной линии. Ширина линии парамагнитного резонанса зависит от ряда причин, большинство которых было рассмотрено выше, но несколько факторов специфичны именно для парамагнитных твердых тел. Согласно принципу неопределенности энергия состояния частицы может быть определена с точностью до величины ΔЕ ≥ h/Δτ, где Δτ - время пребывания частицы в данном состоянии. В процессе парамагнитного резонанса частицы изменяют свое состояние. После снятия индуцирующего излучения система спинов возвращается в состояние термодинамического равновесия за счет релаксационных процессов. В парамагнетиках эти релаксационные процессы связаны с обменом энергией между частицами и тепловыми колебаниями решетки. Этот процесс называют спин-решеточной релаксацией и характеризуют его средним временем τс.р. За это время возбужденная система спинов, обмениваясь фононами с кристаллической решеткой, практически возвращается в состояние равновесия. Таким образом, минимальная ширина линии определяется соотношением Δνл ≥ 1/τc.p.
Величина τс.р для парамагнетиков существенно зависит от температуры, изменяясь от десятых долей секунды при T = 4,2°К до микросекунд при комнатных температурах.
Значительно более серьезный вклад в ширину линии парамагнитного резонанса вносят процессы спин-спиновой релаксации - взаимодействия частиц друг с другом. Этот вид взаимодействия обусловлен наличием собственных электрических и магнитных полей атомов и ионов, воздействию которых подвергаются ионы, расположенные в ближайших узлах решетки. Спин-спиновая релаксация также характеризуется некоторым средним временем τс.с, которое для парамагнитных веществ имеет порядок 10-8 сек. Расширение линии ЭПР за счет спин-спиновой релаксации достигает нескольких десятков мегагерц.
Зеемановское расщепление уровней в рубине. На рис. 8-8 показаны диаграммы расщепления основного энергетического уровня рубина, помещенного во внешнее магнитное поле. Как уже было сказано, магнитные свойства рубина определяются наличием в кристалле парамагнитных ионов Сr3+. Хром (атомный номер 24) имеет электронную конфигурацию 1s2 2s2 2р6 3s2 3р6 3d5 4s1. Незаполненными остаются оболочки 3d и 4s. В рубине хром, замещая атом Аl, трехвалентен. Валентные связи обеспечиваются одним 4s и двумя 3d электронами. Три оставшихся в оболочке 3d электрона обусловливают магнитные свойства иона Сr3+. Для основного состояния S = 3/2; L = 3; J = 3/2. Следовательно, свободный ион должен иметь 2J + 1 = 4 зеемановских уровня. В кристалле орбитальный момент МL сильно подавлен и четыре зеемановских уровня определяются спинами иона Сr3+ (2S + 1 = 4). В результате действия внутреннего электрического поля наблюдается нулевое расщепление (при нулевом внешнем магнитном поле) уровней на два дублета, соответствующих квантовым числам mJ = ±1/2 и mJ = ±3/2. Энергетический зазор между этими дублетами при В = 0 соответствует частоте перехода ν = 11,4 Ггц.
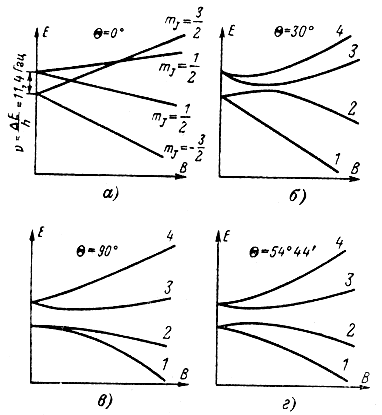
Рис. 8-8. Расщепление энергетических состояний рубина в магнитном поле
Как видно из рис. 8-8, а, в случае совпадения направления вектора В внешнего магнитного поля с осью симметрии кристалла рубина (Θ = 0) наблюдается линейная зависимость E = f(B). В иных случаях (Θ ≠ 0) эта зависимость нелинейна, в особенности в области слабых и средних значений магнитного поля. В зависимости от угла Θ изменяется и характер изменения E = f(В) для различных уровней.
Важно отметить, что при нарушении линейной зависимости теряют смысл квантовые числа mJ. Поэтому и на диаграммах рис. 8-8, б, в и г энергетические уровни обозначены просто цифрами, начиная с наиболее низкого. Понятно, что при этом теряет смысл и правило отбора, разрешающее переходы между уровнями только при условии, что квантовое число mJ меняется на ±1. Таким образом, в области нелинейной зависимости E = f(В) запрещенные переходы становятся разрешенными. Вернее, для каждого значения В и угла Θ может быть вычислена вероятность того или иного перехода. В нелинейной области эта вероятность для любого перехода достаточно велика или, как говорят, здесь наблюдаются сильно разрешенные переходы.
Для квантовых СВЧ приборов особый интерес представляет случай, иллюстрируемый рис. 8-8, г. Кривые E = f(B) для этого случая симметричны относительно средней линии, что весьма удобно для реализации схемы двойной накачки (см. § 7-4). Поэтому угол Θ = 54°44′ в литературе часто называют углом двойной накачки.
В заключение следует еще раз отметить, что на рис. 8-8 показано зеемановское расщепление основного наиболее низкого энергетического уровня и переходы между различными подуровнями соответствуют явлениям парамагнитного резонанса, лежащего в области сверхвысоких частот.
8-4. Квантовый парамагнитный усилитель
Определение. Квантовым парамагнитным усилителем (КПУ) называют такое устройство, в котором увеличение энергии электромагнитной волны происходит за счет индуцированного излучения при парамагнитном резонансе вещества, находящегося в активном состоянии (характеризуемого отрицательной температурой).
Вследствие когерентности индуцированного излучения с подводимыми ко входу усилителя электромагнитными колебаниями усиленные колебания на выходе устройства сохраняют частоту, поляризацию и направление распространения.
Устройство. Существует несколько типов конструкции квантовых парамагнитных усилителей: резонаторные усилители, которые в свою очередь делятся на резонаторные усилители проходного и циркуляторного типов, а также квантовые усилители бегущей волны.
Устройство резонаторного КПУ представлено на рис. 8-9. Парамагнитный кристалл помещен в специальный двухчастотный резонатор, один из возможных вариантов конструкции которого показан на рис. 8-10. Отрезок волновода длиной nλн/2, где λн - длина волны типа ТЕ10 в волноводе на частоте накачки, настроен на частоту сигнала накачки. Резонатором для усиливаемого сигнала служит отрезок полосковой линии длиной λс/4, где λс - длина волны ТЕМ на частоте сигнала.
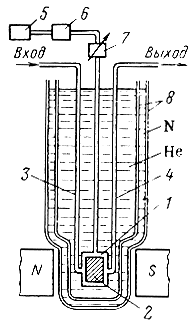
Рис. 8.9. Устройство резонаторного КПУ проходного типа. 1 - двухчастотный резонатор; 2 - активное вещество; 3 - входной фидер; 4 - выходной фидер; 5 - генератор накачки; 6 - ферритовый вентиль; 7 - аттенюатор; 8 - сосуды Дьюара
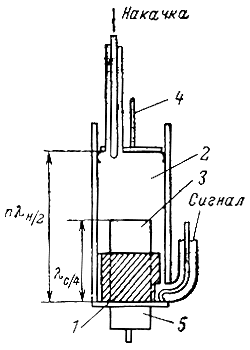
Рис. 8-10. Устройство двухчастотного резонатора. 1 - активное вещество; 2 - отрезок волновода - резонатор накачки; 3 - полосковая линия - резонатор сигнала; 4 - настройка резонатора накачки; 5 - настройка резонатора сигнала
Усиливаемый сигнал подводится к резонатору через входной волноводный или коаксиальный фидер, проходит через активное вещество и через выходной фидер отводится в нагрузку. Такое устройство резонатора используется в усилителях проходного типа.
В усилителях циркуляторного (отражательного) типа для ввода и вывода сигнала используется один и тот же фидер (рис. 8-11). Для развязки входной и выходной цепей используется специальное устройство - ферритовый циркулятор. Особенность этого устройства состоит в том, что сигнал из входного плеча 1 может попасть только в плечо 2, ведущее к резонатору, а отраженный сигнал из плеча 2 - только в плечо 3, соединяемое с нагрузкой. Развязка между входной и выходной линиями (плечи 1 и 3) обычно составляет 25-30 дб.
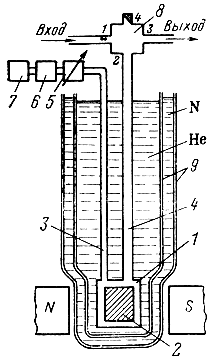
Рис. 8-11. Устройство резонаторного КПУ отражательного типа. 1 - двухчастотный резонатор; 2 - активное вещество; 3 - фидер накачки; 4 - фидер сигнала; 5 - аттенюатор; 6 - ферритовый вентиль; 7 - генератор накачки; 8 - ферритовый циркулятор; 9 - сосуды Дьюара
Иную конструкцию имеет колебательная система в КПУ бегущей волны (рис. 8-12). Усиливаемый сигнал подводится к отрезку волновода, внутри которого расположена замедляющая система штыревого или какого-либо иного типа (рис. 8-13). По одну сторону от замедляющей структуры размещается парамагнитный кристалл, а по другую - вентильный кристалл, обеспечивающий невзаимность устройства. Применение замедляющей структуры позволяет уменьшить скорость электромагнитной волны в десятки или сотни раз и тем самым получить нужную эффективность взаимодействия волны с активным веществом при длине парамагнитного кристалла, в десятки или сотни раз меньше той, которая потребовалась бы для того же эффекта в свободном пространстве.
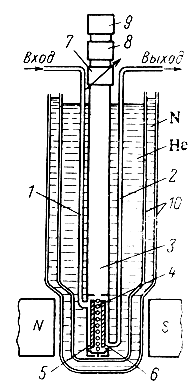
Рис. 8-12. Устройство КПУ бегущей волны. 1 - входной фидер сигнала; 2 - выходной фидер сигнала; 3 - волновод накачки; 4 - замедляющая система; 5 - активное вещество; 6 - вентильный кристалл; 7 - аттенюатор; 8 - ферритовый вентиль; 9 - генератор накачки; 10 - сосуды Дьюара
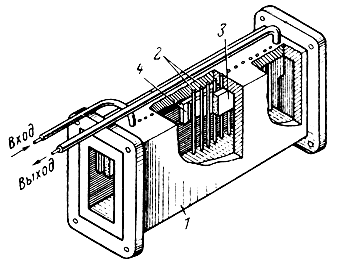
Рис. 8-13. Устройство замедляющей системы КПУ бегущей волны. 1 - волновод; 2 - штыри замедляющей системы; 3 - активное вещество; 4 - невзаимное устройство
Активное вещество располагают в той части замедляющей системы, где высокочастотное магнитное поле, создаваемое сигналом, имеет круговую поляризацию. Это обеспечивает так называемое невзаимное взаимодействие поля усиливаемого сигнала с парамагнитным кристаллом: электромагнитная волна, распространяющаяся от входа замедляющей системы к ее выходу, эффективно взаимодействует с веществом, вызывая интенсивное индуцированное излучение, связанное с парамагнитным резонансом. Волна, отраженная от выхода замедляющей системы, с парамагнитным кристаллом практически не взаимодействует.
Эффект невзаимного взаимодействия усиливается применением вентильного кристалла, интенсивно поглощающего отраженную волну и практически не создающего затухания для волны, движущейся в прямом направлении.
При любой конструкции колебательной системы к парамагнитному кристаллу через отдельный волноводный или коаксиальный фидер подводится от специального генератора сигнал накачки. Вентильное устройство служит для защиты генератора накачки от воздействия отраженной от колебательной системы волны. Аттенюатор используется для регулирования уровня мощности накачки, подводимой к парамагнитному кристаллу.
Как видно из рис. 8-9, 8-11 и 8-12, активное вещество вместе с колебательной системой и частью подводящих фидерных линий помещается в сосуд, содержащий жидкий газ. Такие сосуды, называемые сосудами Дьюара, представляют собой контейнеры с двойными стенками, из пространства между которыми откачан воздух. Для поддержания очень низкой температуры жидкого гелия (4,2°К) внутренний сосуд помещен во внешний сосуд Дьюара, заполненный жидким азотом (Т = 77°K.
Глубокое охлаждение рабочего вещества КПУ и колебательной системы необходимо по ряду причин.
Во-первых, снижение температуры рабочего вещества до температуры жидкого гелия позволяет резко увеличить разность населенностей на рабочем переходе и получить в КПУ достаточно большие коэффициенты усиления (20-30 дб).
Вторая причина глубокого охлаждения усилителя - уменьшение интенсивности тепловых процессов в активном веществе и соответствующее увеличение времени τс.р релаксации системы. При низких температурах, таким образом, для получения нужного коэффициента инверсии населенностей требуется меньшая мощность сигнала накачки.
И, наконец, глубокое охлаждение позволяет существенно снизить уровень собственных шумов усилителя, природа которых имеет в основном тепловой характер (тепловое излучение активного вещества, стенок резонатора, волноводов и т. п.).
Постоянное магнитное поле образуется магнитами, которые могут быть расположены вне системы охлаждения. Вес таких магнитных систем достигает десятков и сотен килограмм. В современных конструкциях квантовых усилителей для этой цели используются электромагниты с токопроводом из сверхпроводящих материалов, размещаемые вместе с резонатором в сосуде с жидким гелием. Такие магниты не нуждаются в постоянных источниках тока. После возбуждения тока их обмотки закорачиваются сверхпроводящей перемычкой. Вес таких магнитных систем невелик и значительно меньше веса охлаждающей системы.
Активное вещество. В качестве активного вещества в квантовых парамагнитных усилителях может быть использован ряд кристаллов: рутил (ТiO2), вольфраматы (MgWO4; ZnWO4; CdWO4) с примесью ионов Сr3+ или Fe3+ и другие соединения. Однако наиболее широкое применение находят кристаллы рубина.
Система рабочих уровней. Выбор рабочих энергетических уровней в рубине во многом зависит от рабочей частоты усилителя.
В диапазоне волн 3-5 см (6-10 Ггц) чаще всего используются четыре энергетических уровня кристалла рубина, ориентированного относительно внешнего магнитного поля под углом Θ = 54°44' (рис. 8-14). Энергетическая накачка ведется пушпульно: одновременно на переходах 1 → 3 и 2 → 4, частоты которых равны (ν13 = ν24) в широком диапазоне изменения магнитного поля В. При этом заселяется верхний уровень Е3 рабочего перехода 3 → 2 и обедняется его нижний уровень Е2.
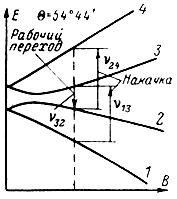
Рис. 8-14. Четырехуровневая система в кристалле рубина
Такой метод накачки, как уже упоминалось в гл. 7, позволяет получить инверсное состояние системы при условии, что частота накачки будет больше частоты сигнала (ν13 > ν32), а не удвоенной частоты сигнала, как это требуется при использовании трехуровневой системы. Таким образом, при рабочей частоте 6-10 Ггц в качестве генератора накачки может быть использован, например, клистронный генератор с частотой f ≥ 12÷20 Ггц.
На более длинных волнах (λ > 5 см; ν < 6 Ггц) чаще всего используют системы из трех рабочих уровней при ориентации кристалла относительно поля В под углом Θ = 90°. На рис. 8-15, а показаны рабочий переход 4→3 и вспомогательный переход накачки 2→4 или, что то же самое 1→4, так как в слабом магнитном поле уровни Е1 и Е2 практически сливаются. Как видно из рисунка, ΔE14 > 2ΔE43. Этот режим выгоден возможностью использования слабого магнитного поля, порядка 200-700 гс.
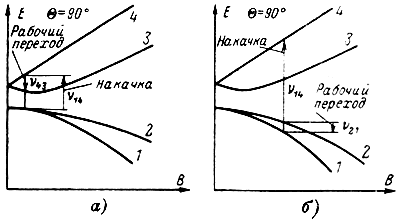
Рис. 8-15. Режимы работы в системе из трех уровней рубина
Наибольший коэффициент инверсии населенностей достигается в случае использования режима, показанного на рис. 8-15, б.
Ввиду слабого расщепления уровней E1 и Е2 в этом режиме необходимо использование более сильных магнитных полей, что однако окупается существенным увеличением коэффициента инверсии, а следовательно, и коэффициента усиления.
Эквивалентная схема. Квантовый усилитель резонаторного типа можно представить простой эквивалентной схемой (рис. 8-16).
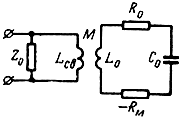
Рис. 8-16. Эквивалентная схема КПУ резонаторного типа
Индуктивность L0 и емкость С0 образуют колебательный контур с резонансной частотой
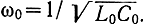
Омические потери в этом контуре характеризуются резистором R0. Величина Z0 - волновое сопротивление подводящего фидера.
Высокочастотные колебания, подлежащие усилению, при подаче на вход усилителя вызывают индуцированное излучение вещества с инверсной населенностью. Это свойство активного вещества характеризуется отрицательным сопротивлением - RM. В рабочем режиме |Rм| >> |R0|.
Величина резистора - RM естественно зависит от физических параметров активного вещества, формы линии магнитного резонанса и других факторов.
Для дальнейших рассуждений и при определении основных параметров квантового усилителя удобно пользоваться не величиной отрицательного резистора - RM, а понятием отрицательной магнитной добротности.
Отрицательная магнитная добротность, характеризующая усилительные свойства активного вещества, может быть на основании эквивалентной схемы (рис. 8-16) определена следующей формулой:
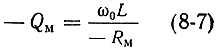
или иначе
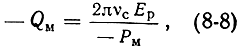
здесь Eр - энергия, запасаемая в резонаторе; Рм - мощность, излучаемая активным веществом под действием сигнала; νc - центральная частота линии магнитного резонанса на рабочем переходе (при точной настройке контура 2πνc = ω0).
Энергия Eр, запасаемая в резонаторе, может быть найдена на основании известного из физики соотношения
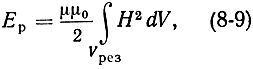
где μ - относительная магнитная проницаемость среды; μ0 - магнитная проницаемость вакуума; H - напряженность высокочастотного магнитного поля в резонаторе; dV - элементарный объем резонатора. Интегрирование производится по всему объему резонатора Vрез.
Для мощности, излучаемой активным веществом, можно записать:
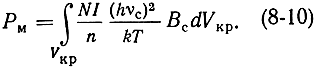
В этом выражении N - полное число частиц на всех n - рабочих уровнях; I - коэффициент инверсии, определяемый соотношением (7-26); νc - частота сигнала; Вс - вероятность индуцированных сигналом переходов; dVкр - элементарный объем рабочего вещества. Интегрирование производится по всему объему рабочего вещества в резонаторе.
Следует иметь в виду, что излучаемая мощность зависит от частоты сигнала в соответствии с фактором формы линии парамагнитного резонанса. Учитывая это обстоятельство и используя выражения (8-9) и (8-10), можно записать выражение для магнитной добротности в виде
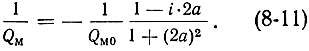
В этом выражении а = Δν/Δνл - отношение расстройки частоты сигнала от центральной частоты линии (Δν = νc - νл) к ширине линии Δνл, a Qм0 - модуль отрицательной магнитной добротности на резонансной частоте (2πνc = ω0)
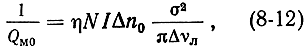
здесь N - полное число частиц на всех n уровнях; I - коэффициент инверсии рабочего перехода; Δn0 - разность относительных населенностей уровней рабочего перехода при термодинамическом равновесии; σ2 - коэффициент вероятности рабочего перехода частиц (при сильноразрешенном переходе σ2 ≈ 1); η - фактор заполнения резонатора активным веществом, определяющий эффективность использования высокочастотного магнитного поля и равный отношению энергии магнитного поля, запасенной в активном веществе, к магнитной энергии, запасенной во всем резонаторе.
Модуль магнитной добротности равен:
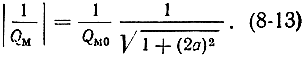
Анализируя соотношения (8-11) - (8-13), можно сделать следующие выводы, важные для дальнейшей оценки параметров квантового усилителя.
Величина 1/Qм комплексная ее действительная часть характеризует усилительные свойства активного вещества, помещенного в резонатор, а мнимая часть - дисперсионные свойства. При точной настройке частоты сигнала νc на центральную частоту линии νл (Av = νc - νл = 0) магнитная добротность - действительная величина. При расстройке
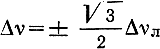
величина |1/QM| уменьшается в 2 раза.
В условиях резонанса величина 1/Qм зависит от ряда важнейших физических и конструктивных параметров. При конструировании квантовых усилителей стремятся получить наибольшее значение величины |1/Qм|. Как видно из (8-12), для удовлетворения этих требований необходимо наиболее эффективно использовать объемный резонатор: стремиться заполнить его целиком, обеспечивая при этом ориентацию высокочастотного магнитного поля в направлении, оптимальном для индуцирования рабочих переходов. В этом случае η→1.
Желательно также увеличивать концентрацию спинов N, однако при этом следует учитывать, что в этом направлении имеется оптимум. Чрезмерное увеличение концентрации N приводит к уширению линии за счет спин-спинового взаимодействия, увеличению спин-решетчатых и кросс-релаксационных эффектов, что в свою очередь уменьшает коэффициент инверсии I и требует увеличения мощности накачки. Обычная величина концентрации спинов в активном веществе имеет порядок N ≈ 1019÷1020 см-3.
Для увеличения коэффициента инверсии I и величины Δn0 применяют глубокое охлаждение рабочего вещества. Как следует из классической статистики (7-7)
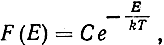
чем выше температура системы, тем положе экспонента, описывающая распределение частиц по энергетическим состояниям. Разность населенностей рабочих уровней в инверсном состоянии по порядку величины такая же, как и разность населенностей в условиях термодинамического равновесия. В диапазоне сверхвысоких частотой при комнатных температурах величина разности населенностей имеет порядок 10-4. При низких температурах, например при температуре жидкого гелия (T = 4,2°К), экспонента (7-7) становится крутой и разность населенностей существенно возрастает.
Немаловажное значение для увеличения коэффициента инверсии I имеют соотношения частот сигнала и накачки, а также вероятностей релаксационных переходов.
В самом деле на основании выражения (7-38) для коэффициента инверсии можно записать:
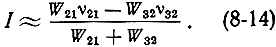
Отсюда, как и из анализа выражения (7-38), следует, что коэффициент инверсии тем больше, чем сильней неравенство W21ν21 > W32ν32 и W21 > W32.
Таким образом,
I ≈ ν21/ν32, (8-15)
где ν32 - частота рабочего перехода 3->-2, а накачка ведется на переходе 1 → 3. Следовательно, коэффициент инверсии I увеличивается с ростом отношения частоты накачки к частоте сигнала ν13/ν32, а также с увеличением времени жизни частиц на уровне Е3 (W32 мало) и интенсивности релаксационных переходов 2 → 1 (W21 велико), обедняющих нижний уровень рабочего перехода.
Обычно квантовые усилители работают с коэффициентами инверсии I ≈ 1÷4.
Как следует из (8-12), желательно также сужать ширину линии Δνл парамагнитного резонанса. Однако, как это было показано ранее, величина Δνл определяется рядом физических параметров, произвольное управление которыми не всегда возможно. Кроме того, величина Δνл не должна ограничивать полосу пропускания квантового усилителя. Как правило, однако, ширина линии Δνл, имеющая величину порядка нескольких десятков или сотен мегагерц, значительно превышает полосу усиливаемых частот.
При упомянутых выше численных значениях величин, входящих в (8-12), величина магнитной добротности в реальных устройствах Qм ≈ 100÷250.
В заключение следует отметить, что величина магнитной добротности весьма слабо зависит от изменения величины магнитного поля, стабильности частоты накачки и т. д. Иначе говоря, активные вещества, используемые в квантовых парамагнитных усилителях, отличаются достаточно высокой стабильностью, обеспечивая устойчивое усиление при удовлетворении необходимых требований.
8-5. Параметры и характеристики квантовых парамагнитных усилителей
Основными параметрами квантовых парамагнитных усилителей служат: рабочая частота νc или длина волны λс сигнала, для усиления которого рассчитан усилитель; частота νн или длина волны λн сигнала накачки; полоса пропускания усилителя Δνc; коэффициент КР усиления сигнала по мощности; величина магнитной индукции В0 или напряженности Н0 внешнего постоянного магнитного поля; температура рабочего вещества; фактор шумов или температура шумов и динамический диапазон усилителя.
Выбор рабочего вещества и конструкции сверхвысокочастотных узлов во многом определяется рабочей частотой сигнала.
В свою очередь конструктивное решение существенно влияет на величины коэффициента усиления, полосы усиливаемых частот и других параметров. Рассмотрим основные параметры КПУ, обсуждая попутно некоторые конструктивные особенности усилителей различных типов.
Рабочая частота сигнала. Квантовые парамагнитные усилители используются для усиления сигналов в достаточно широком диапазоне сверхвысоких частот: от 0,6 до 75 Ггц или соответственно в диапазоне волн от 0,4 до 50 см.
В длинноволновой части этого диапазона, а также на волнах λ ≈ 1÷6 см в качестве рабочего вещества обычно используют рубин.
На волнах короче 1 см применяют рутил с примесью железа или хрома, который, впрочем, находит применение и в более длинноволновой части диапазона.
Как уже отмечалось выше, на более длинных волнах используется энергетический спектр кристалла рубина, тригональная ось которого располагается перпендикулярно направлению магнитного поля (Θ = 90°). В области более коротких волн обычно используют систему четырех уровней кристалла рубина, ориентированного относительно магнитного поля под углом Θ = 54°44'.
Частота сигнала накачки. Энергетическая накачка в КПУ обычно осуществляется с помощью клистронных генераторов с длиной волны λн ≈ 2,0÷2,6 см - в дециметровом диапазоне волн и λн ≈ 0,2÷1,3 см - в сантиметровом и миллиметровом диапазонах. Как было показано выше, частота накачки должна по крайней мере в 2 раза превышать частоту сигнала (νн/νc > 2). Это отношение наиболее трудно осуществимо в коротковолновой части диапазона, где обычно νн/νc ≈ 2. В дециметровом диапазоне волн величина отношения νн/νc может достигать 15 и более.
Температура рабочего вещества. Обычно квантовые парамагнитные усилители работают при температуре жидкого гелия (T = 4,2°К). В некоторых устройствах при откачке паров гелия до давления примерно 5-20 мм рт. ст. температура понижается до 1,5-2°К. Устройства, предназначенные для получения и поддержания низкой температуры, называют криостатами. Как уже отмечалось в § 8-4, жидкий гелий и жидкий азот заливаются в специальные стеклянные или металлические сосуды Дьюара. Волноводные и коаксиальные фидеры, а также другие элементы СВЧ тракта, размещаемые в жидком гелии, выполняют из нержавеющей стали или латуни.
Для КПУ, эксплуатируемых в полевых условиях, используются специальные установки для ожижения гелия с замкнутым циклом.
Необходимость применения криостатов приводит к существенному усложнению конструкции квантовых усилителей, которое, однако, окупается рядом других достоинств.
Величина индукции постоянного магнитного поля лежит в пределах 0,1-5 кгс, увеличиваясь по мере укорочения рабочей волны.
Выше уже отмечалось, что для создания постоянного магнитного поля используются как внешние магнитные системы, располагаемые вне криостата, так и системы электромагнитов (или постоянных магнитов), размещаемые вместе с колебательной системой в сосуде с жидким гелием. Внешние магниты, используемые обычно в лабораторных установках, весьма громоздки и достигают веса в несколько сот килограмм. Вес магнитов, размещаемых в криостате, как правило, значительно меньше, так как требуются меньшие зазоры между полюсными наконечниками, а диаметр самих наконечников для создания однородного магнитного поля также может быть существенно сокращен. Конструкция электромагнитов для использования в среде жидкого гелия весьма проста: на латунный каркас наносят обычно неравномерную уплотненную на концах, сверхпроводящую обмотку из нескольких тысяч витков ниобиевой проволоки. После возбуждения тока обмотка соленоида закорачивается также сверхпроводящей перемычкой.
Коэффициент усиления и полоса пропускания КПУ существенным образом зависят от конструкции их колебательной системы. Рассмотрим поэтому эти параметры применительно к основным типам квантовых усилителей.
Однорезонаторный КПУ. Устройство однорезонаторных усилителей проходного и отражательного типов было показано на рис. 8-9 - 8-11. Наибольшее распространение получил отражательный усилитель, в котором эффективность взаимодействия поля с активным веществом примерно в 2 раза больше, чем в усилителе проходного типа. Это объясняется тем, что в отражательном усилителе сигнал излучается лишь в направлении выходного фидера, в то время как в проходном усилителе это излучение происходит как через входное, так и через выходное отверстия связи.
Усилительные свойства КПУ, как это было показано в предыдущем параграфе, характеризуются магнитной добротностью вещества Qм. Использование этой величины в сочетании с эквивалентной схемой колебательной системы усилителя позволяет с помощью хорошо известных из теории цепей и радиотехники методов найти величину КР - коэффициента усиления, уравнение частотной характеристики, величину полосы пропускания и другие параметры.
В усилителе отражательного типа усиленным является сигнал, отраженный от резонатора, т. е. тот сигнал, который получился на выходе резонатора в результате суммирования входного сигнала и индуцированного излучения активного вещества, развившегося под воздействием пришедшего сигнала. Таким образом, коэффициент усиления сигнала по мощности равен квадрату модуля коэффициента отражения
К = |Г|2. (8-16)
Как известно из теории цепей,
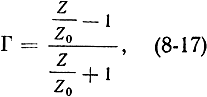
где
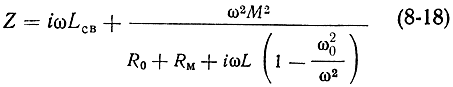
- сопротивление петли связи плюс сопротивление контура, пересчитанное ко входу линии связи (см. рис. 8-16).
Введем понятия добротности резонатора
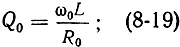
добротности устройства связи
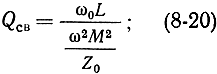
добротности линии парамагнитного резонанса
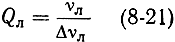
и относительной расстройки частоты сигнала νс = ωс/2π от резонансной частоты ν0 = ω0/2π контура
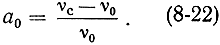
С помощью этих величин, пользуясь методами анализа теории цепей, можно получить выражение для коэффициента усиления при условии ν0 = νл:
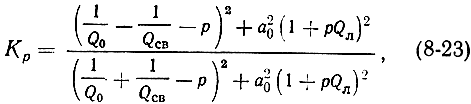
где
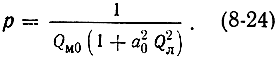
Для случая резонанса (νc = ν0 = νл) (8-23) принимает вид:
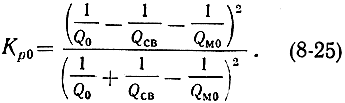
Формула (8-23) описывает частотную характеристику усилителя, которая по форме близка к резонансной кривой одиночного контура.
Из выражения (8-25) можно, в частности, видеть, что Кр0 > 1 в том случае, когда мощность индуцированного излучения превышает потери в резонаторе (Qм0 < Q0); Кр0 >> 1 при условии, что 1/Qм0 ≤ 1/Q0 + 1/QCB. В отсутствие активного вещества (Qм0 → ∞) подводимый к усилителю сигнал претерпевает ослабление (Кр0 < 1).
С помощью формулы (8-23) можно установить связь между величиной полосы пропускания усилителя Δνc на уровне Кр = Кр0/2 и величиной Кр0
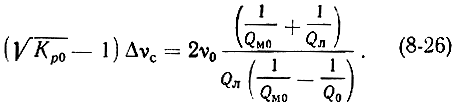
При условии, что величина Δνл много шире полосы пропускания нагруженного резонатора, выражение (8-26) можно переписать в виде
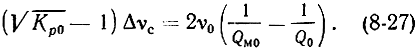
Приближенно можно полагать, что в этом случае полоса пропускания усилителя определяется полосой Δνн нагруженного резонатора. Для Кp0 >> 1 можно записать:
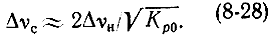
Это выражение, как и предположения, высказанные выше, справедливо для длинноволновой части диапазона, где обычно выполняется неравенство Δνн << Δνл.
В коротковолновой области часто Δνл << Δνн и полоса пропускания усилителя определяется величиной Δνл
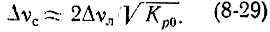
Из выражений (8-28) и (8-29) видно, что произведение
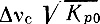
равно некоторой определенной величине, что характерно вообще для регенеративных усилителей. С увеличением Кр0 полоса пропускания усилителя сужается.
Величина Кр0 для одноконтурных КПУ обычно не превышает 20-25 дб, а величина полосы пропускания лежит в пределах от десятых долей до единиц мегагерц. Для расширения полосы пропускания часто в КПУ используют систему из двух связанных контуров.
Двухрезонаторный усилитель. В общем случае эквивалентная схема двухрезонаторного КПУ имеет вид, показанный на рис. 8-17.
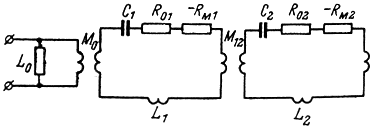
Рис. 8-17. Эквивалентная схема двухрезонаторного КПУ
Первый резонатор может быть пассивным, т. е. не содержащим активное вещество. В этом случае коэффициент усиления и полоса пропускания определяются следующими выражениями:
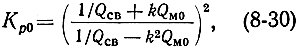
где
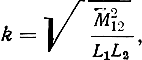
характеризует добротность связи первого резонатора с линией
Δνc √√Kp0 - 1 = ν0 √2 (√2 - 1) /Qм0 + Qл. (8.31)
Для усилителя, в котором оба резонатора содержат активное вещество, полоса пропускания увеличивается в √2 по сравнению с величиной, рассчитанной по формуле (8-31).
В общем случае использование системы из двух связанных контуров позволяет расширить полосу пропускания в 1,5-2 раза.
Квантовый усилитель бегущей волны. Дальнейшее, по сравнению с двухрезонаторным КПУ, расширение полосы пропускания может быть достигнуто с помощью цепочки нескольких связанных резонаторов. Однако ко времени создания квантовых усилителей СВЧ был уже накоплен значительный опыт разработки широкополосных усилительных ламп бегущей волны, в которых применялись различного рода замедляющие системы. Этот опыт с успехом был использован при конструировании квантовых парамагнитных усилителей бегущей волны.
Устройство КПУ бегущей волны и конструкция узла замедляющей системы были показаны на рис. 8-12 и 8-13. Наиболее широкое применение в КПУ нашли замедляющие системы штыревого типа (рис. 8-13). Каждый штырь в такой системе подобен заземленному четвертьволновому вибратору. У основания штыря магнитное поле описывается силовыми линиями в виде концентрических окружностей и по разные стороны гребенчатой структуры образуются области с круговой поляризацией разных знаков. Это означает, что условия эффективного взаимодействия движущейся от входа волны с веществом, а следовательно, и интенсивного индуцированного излучения могут быть получены лишь при размещении активного вещества по одну сторону гребенки. В то же время отраженная волна, движущаяся ко входу, образует со стороны активного вещества поле, знак поляризации которого неблагоприятен; энергия этой волны поглощается активным веществом. За счет этого эффекта достигается ослабление отраженной волны на 15-20 дб.
Помимо этого, как уже было сказано ранее, по другую сторону замедляющей системы располагают специальные развязывающие элементы, интенсивно поглощающие отраженную волну. В качестве такого невзаимного элемента может быть использован тот же рубин, но с повышенной концентрацией Сr (до 1-2%). Такой элемент обеспечивает затухание обратной волны порядка 30 дб. Более высокие развязки (> 100 дб) получают при использовании в качестве невзаимного элемента дисков из гранатового феррита.
Величину коэффициента усиления КПУ бегущей волны можно рассчитать методами обычного анализа цепей с использованием, как и ранее, понятия магнитной добротности вещества:
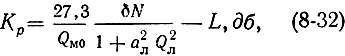
здесь
δ = c/υгр (8-33)
- коэффициент замедления волны;
N = l/λ0, (8-34)
где l - длина замедляющей системы, λ0 - длина волны в свободном пространстве;
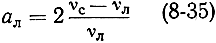
- относительная расстройка частоты сигнала от центральной частоты линии парамагнитного резонанса; L - потери в замедляющей системе, выраженные в децибелах.
В условиях резонанса (νс = νл)
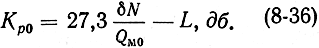
Как и в любом регенеративном усилителе, ширина полосы пропускания КПУ бегущей волны связана с величиной коэффициента усиления
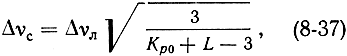
здесь, как и ранее, величины Кр0 и L выражены в децибелах.
Приведенные выше выражения справедливы в том случае, если в КПУ выполняется режим бегущей волны. Для обеспечения этого требования затухание отраженной волны должно удовлетворять условию
Lотр >> Kp Г12 Г22, (8-38)
где Г1 и Г2 - коэффициенты отражения на входе и выходе замедляющей системы.
В КПУ бегущей волны величина Кр0 достигает 50 дб, а полоса пропускания (при δ ≈ 200÷300) составляет 20-30% от центральной рабочей частоты.
Динамическим диапазоном называют диапазон изменения мощности входного сигнала, в пределах которого квантовый усилитель обеспечивает требуемое усиление сигнала и его выделение на выходе устройства.
В области маломощных сигналов динамический диапазон ограничен величиной собственных шумов квантового усилителя. Входной сигнал, мощность которого ниже некоторой пороговой величины, не может быть выделен на выходе усилителя на фоне шумов КПУ.
С другой стороны, динамический диапазон ограничивается режимом насыщения рабочего перехода активного вещества. При подаче на вход усилителя мощного сигнала развивается интенсивный процесс индуцированных переходов частиц на рабочем переходе, населенность верхнего уровня этого перехода резко уменьшается и коэффициент усиления падает. При достаточно большой мощности входного сигнада рабочий переход может оказаться в режиме насыщения, когда населенности верхнего и нижнего уровней будут примерно равны.
По окончании сигнала инверсная населенность рабочего перехода восстанавливается лишь по прошествии некоторого времени, определяемого в основном временем спин-решетчатой релаксации.
На рис. 8-18 показана зависимость коэффициента усиления от мощности входного сигнала. Верхняя граница динамического диапазона обычно определяется по мощности, соответствующей уменьшению величины Кр0 в два раза. Для КПУ величина Pвх.макс ≈ 10-6 вт.
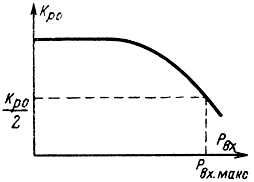
Рис. 8-18. Зависимость коэффициента усиления от мощности входного сигнала
Величина динамического диапазона КПУ может быть расширена, с одной стороны, за счет уменьшения уровня собственных шумов, а с другой - за счет увеличения объема рабочего вещества и числа активных частиц, а также за счет уменьшения времени спин-решетчатой релаксации.
Собственные шумы квантового парамагнитного усилителя определяются, главным образом, спонтанным излучением активного вещества и тепловым излучением стенок резонатора. Как уже упоминалось в гл. 7, уровень спонтанного излучения в диапазоне СВЧ очень мал; его величина имеет величину порядка hνc/k. При температуре жидкого гелия уровень тепловых шумов резонатора также невелик. В общем случае спектральная плотность мощности шумов КПУ бегущей волны может быть рассчитана по формуле
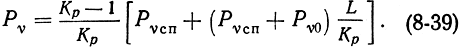
Соответственно температура шумов равна:
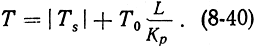
В выражениях (8-39) и (8-40) Pνсп - спектральная плотность мощности спонтанных шумов; Pν0 - спектральная плотность тепловых шумов; Ts - отрицательная температура рабочего перехода; Т0 - абсолютная температура резонатора; Кр и L выражены в децибелах.
Температура шумов собственно квантового усилителя чрезвычайно низка, она не превышает единиц °К.
Применение КПУ на входе радиоприемных устройств приводит к существенному увеличению их чувствительности, однако следует иметь в виду, что в реальных устройствах к собственным шумам КПУ добавляются шумы антенны, фидерных устройств и др.

© RATELI.RU, 2010-2020
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
