
2.1. Уравнения и матрицы восьми полюсника. Принцип нормирования уравнений
Стационарные процессы на внешних полюсах восьми полюсника описываются с помощью комплексных амплитуд напряжений Ui и токов Ii или комплексных амплитуд падающих UПi и отраженных UOi волн напряжения (рис. 2.1). Связь между напряжениями (токами) и волнами напряжения определяется равенствами
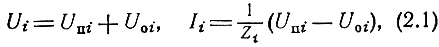
где i = 1, 2, 3, 4 - номера полюсов.
Уравнения передачи, характеризующие связь входных и выходных напряжений, токов и волн напряжения, записываются в матричной форме
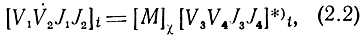
* (В дальнейшем квадратные скобки, обозначающие матрицу, будем опускать в том случае, если принадлежность данного символа к матрице указывается каким-либо другим способом, например, индексом или словами в тексте.)
где символом Vi обозначены комплексные амплитуды напряжения или падающих волн напряжения (Vi=Ui или Vi=UПi), а символом Ji - комплексные амплитуды токов или отраженных волн напряжения (Ji = Ii или Ji=- UОi; индекс t означает операцию транспонирования матриц - строк; [М]χ - матрица Α-параметров [Α]χ или волновая матрица передачи [T]χ индекс χ указывает на принадлежность данных матриц к принятой в (2.2) последовательности напряжений, токов и волн напряжения, т. е. к определенной системе координат (СК). Запись уравнений передачи в виде (2.2) общепринята в литературе. В СК χ записываются все связи между матрицами.
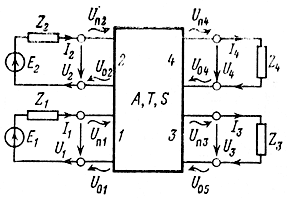
Рис. 2.1. Напряжения, токи, падающие и отраженные волны напряжения восьми полюсника при прямой передаче сигнала
В уравнениях (2.2) Ui, Ii, Uпоi, а следовательно, и элементы матрицы могут быть либо ненормированными, либо нормированными относительно нагрузочных сопротивлений Zi. Нормированные напряжения, токи и волны напряжения имеют смысл корня квадратного из комплексной мощности. При этом элементы матриц становятся безразмерными. Нормированные и ненормированные величины связаны следующими соотношениями
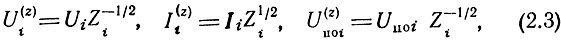
где индекс z означает нормированную величину. Вообще говоря, нормирующими сопротивлениями могут быть любые произвольные сопротивления. Наиболее удобным является нормирование относительно нагрузочных сопротивлений. Запись элементов матриц упрощается при нормировании относительно некоторых характерных сопротивлений (например, характеристических сопротивлений пассивных четырехполюсников, включенных в восьми полюсник). При использовании нормированных величин (2.3) равенства (2.1) приобретают вид
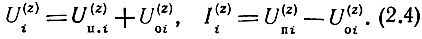
Нетрудно установить связь между нормированными и ненормированными матрицами
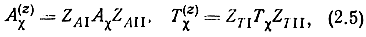
где
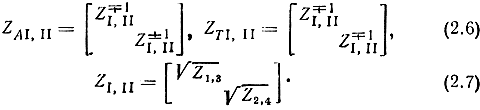
Подставляя матрицы Αχ и Тχ в блочной форме
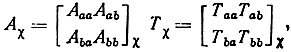
выражения (2.5) можно записать в виде
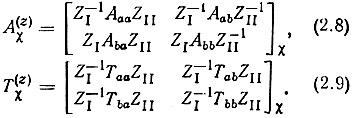
Иногда требуется перенормировать матрицы. Если матрица Αχ была нормирована относительно произвольных сопротивлений ρi то нормирование матрицы Αχ относительно сопротивлений Zi производится с помощью матричного равенства
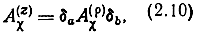
где
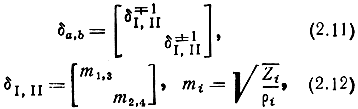
Α(ρ)χ - получена из (2.5) при замене Zt на ρi.
Равенства (2.4) позволяют выразить волновую матрицу передачи через матрицу Α-параметров
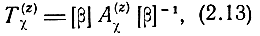
где
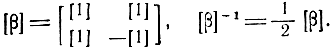
В блочной записи (2.13) имеет вид
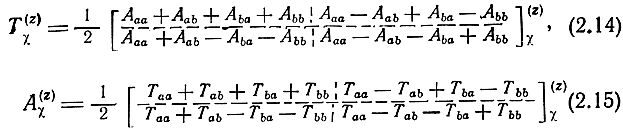
Формулы (2.13) - (2.15) позволяют перейти от Α-параметров к параметрам внешней волновой матрицы передачи, а также обратно. Связь между ними с помощью преобразования подобия (2.14) позволяет сделать вывод об одинаковых собственных значениях матриц Α(z)χ и T(z)χ [31].
С волновой матрицей передачи тесно связана волновая матрица рассеяния, представляющая собой систему коэффициентов в уравнениях
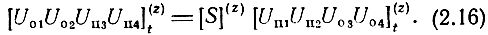
Матрица [S](z) связывает нормированные волны напряжения, расходящиеся от восьми полюсника, с нормированными волнами напряжения, сходящимися к восьми полюснику. В клеточной записи она имеет вид
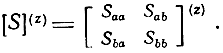
Формулы связи матриц T(z)χ и S(z)χ могут быть представ-лены в виде [30]:
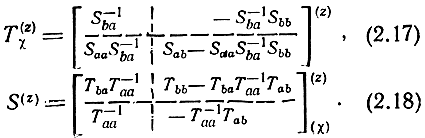

© RATELI.RU, 2010-2020
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
