2.2. Связь между матрицами передачи в различных системах координат

При записи уравнений передачи каскада усилителя с распределенным усилением удобна другая система координат

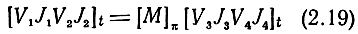
где индекс π означает принадлежность матриц к СК (2.19). Величины в этих уравнениях могут быть также нормированными или ненормированными. Удобство использования данной системы уравнений объясняется тем, что блоки матриц

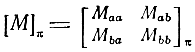
имеют вполне определенный физический смысл. Блоки М_aaπ и М_bbπ характеризуют передачу сигнала в направлении полюсов соответственно 1↔3 и 2↔4, а блоки М_baπ и М_abπ отражают взаимосвязь передающих линий: усиление и обратную передачу сигнала.

Кроме указанных вариантов систем уравнений (2.2) и (2.19) для анализа УРУ с различными структурами могут употребляться и другие системы.

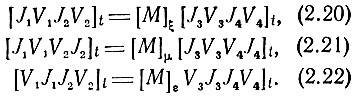
Матрицы в различных СК связаны преобразованиями подобия. Переход к классическим матрицам осуществляется с помощью соотношений

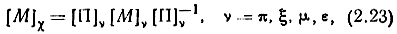
где [Π]_ν - преобразующие матрицы, а [Π]_ν^-1 равны транспонированным [Π]_ν: [Π]^-1_ν = [Π]_νt,

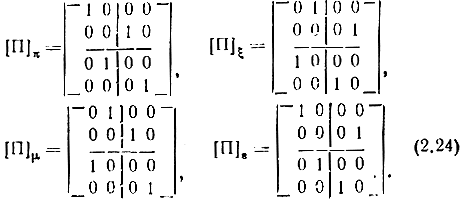
Переход к матрицам в СК π производится по формулам

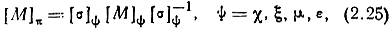
где

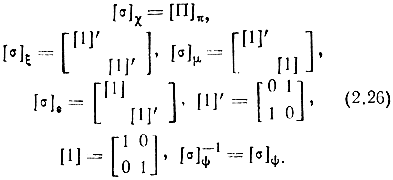
Таким образом, соотношения (2.23) и (2.25) позволяют преобразовывать матрицы [Α] и [T], представленные в различных системах координат.

Для удобства непосредственного использования переходов от одной СК к другой представим уравнения (2.23) и (2.25) в виде матричных равенств. При этом элементы матриц [M]_ν,ψ заменим соответствующими индексами. Тогда (2.23) запишется

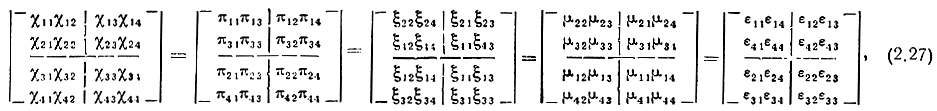
а (2.25) предстанет в виде

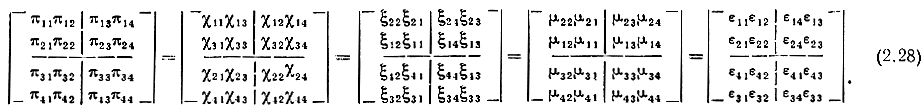
Для нормирования матриц в координатах π, ξ, μ,ε необходимо вначале преобразовать матрицы в координаты χ (2.23), а затем воспользоваться соотношениями (2.5).