2.3. Рабочие коэффициенты передачи каскада УРУ

Рабочие коэффициенты передачи напряжения и тока (1.1) удобно представить в виде элементов матрицы рабочих коэффициентов передачи

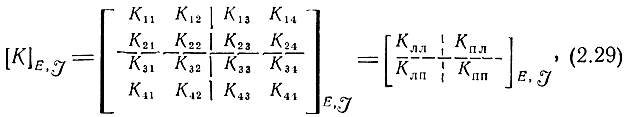
где К_лл и К_лп - блоки, содержащие коэффициенты передачи в прямом направлении (с левых полюсов на левые и с левых полюсов на правые); К_пл и К_пп - блоки коэффициентов передачи в обратном направлении (с правых полюсов на левые и с правых полюсов на правые).

Рабочие коэффициенты передачи, так же как параметры Α, Т, S-матриц, могут быть нормированными или ненормированными. Снабжая индексом (z) рабочие коэффициенты передачи, нормированные относительно нагрузочных сопротивлений, и подставляя (2.3) в (1.1) найдем необходимую связь

Нормированные рабочие коэффициенты передачи достаточно просто выражаются через элементы матрицы рассеяния S^(z)[32]:

Поэтому можно построить алгоритм расчета на ЭЦВМ рабочих коэффициентов передачи, используя стандартные программы перемножения матриц. Допустим, что исходной матрицей является матрица Α-параметров в какой-либо СК (ν=π, ξ, μ, ε), нормированная относительно некоторых сопротивлений ρ_i. Тогда, используя преобразование координат (2.23) и уравнение (2.10), можно с помощью преобразования подобия (2.13) вначале перейти к волновой матрице передачи

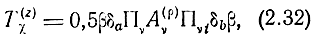
а затем по (2.18) рассчитать элементы матрицы рассеяния и рабочие коэффициенты передачи (2.31).

Из (2.31) легко находятся любые другие характеристики восьми полюсника. Так отношение нормированных комплексных амплитуд напряжений можно определить как отношение элементов какого-либо столбца матрицы [К]^(z)_E. Например, при э. д. с., действующей на полюсах 1,

Входные нормированные сопротивления могут быть найдены при совместном использовании [K]^(z)_E и [K]^(z)_J

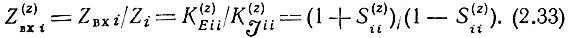
Поскольку схема каскада однородного усилителя с распределенным усилением обладает симметрией относительно вертикальной оси, то рабочие коэффициенты передачи в обратном направлении К_пл и К_пп можно определить из формул для коэффициентов передачи в прямом направлении соответственно К_лп и К_лл, предварительно произведя в них замену Z_1,2↔Z_3,4,4. Если дополнительно к симметрии каскада нагрузочные сопротивления также симметричны, т. е. Z_1,2=Z_3,4 то в соответствии со свойствами симметричного относительно вертикальной оси восьми полюсника [30]

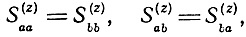
откуда следует, что

Для получения аналитических зависимостей рабочих коэффициентов передачи от параметров четырехполюсников, образующих каскад усилителя, необходимы формулы, представленные через элементы А и Т-матриц [33]. Для получения этих формул запишем уравнения восьми полюсника и уравнения внешних контуров в блочной форме при прямой передаче сигнала

где U_I,II, I_I,II E_I - векторы соответственно напряжений, токов на входных и выходных полюсах и вектор внешних э. д. с. U_I,II = [U_1,3, U_2,4]_t, I_I,II = [I_1,3,I_2,4]_t, E_I = [E₁, E₂]_t, Z_I,II определяются по формуле (2.7). Совместное решение системы (2.34) проведено в [29]:

где матрица

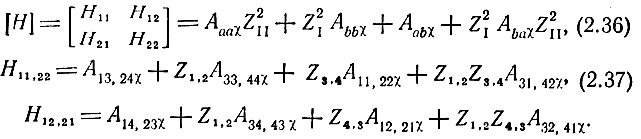
Используя связь между нормированными и ненормированными векторами

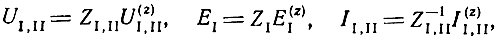
а также (2.8) и (2.36), представим (2.35) в нормированных величинах

где

Обращаясь к формулам связи матриц Α^(z)_χ и T^(z)_χ (2.14),

видим, что

а формулы (2.38) можно выразить через T-параметры

Раскрывая матричные соотношения (2.35), находим

где |H| - определитель матрицы (2.36). При использовании Α-параметров, нормированных относительно сопротивлений, равных нагрузочным, в формулах (2.42) - (2.44) необходимо положить Z_i= 1. При этом рабочие коэффициенты передачи будут нормированными также относительно Z_i. Если Α-параметры нормированы относительно каких-либо сопротивлений, неравных нагрузочным, то и рабочие коэффициенты передачи необходимо считать нормированными относительно этих сопротивлений. Из (2.41) следует:

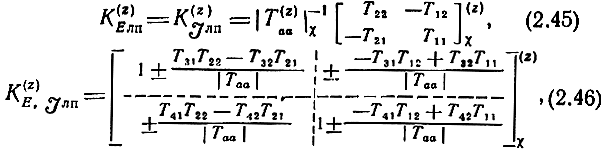
где - определитель блока .

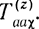Таким образом, любые рабочие коэффициенты передачи каскада УРУ по приведенным соотношениям могут быть получены в аналитическом виде или рассчитаны с помощью ЭЦВМ.