2.4. Определение напряжения на выходе однородного каскада УРУ при действии в k-й секции независимых источников

Для определения коэффициента шума каскада УРУ необходимо знать коэффициенты передачи напряжения от источников, действующих в какой-либо k-й секции, к выходным полюсам 4. Для этого рассмотрим схему каскада, состоящего из n идентичных секций (рис. 2.2).

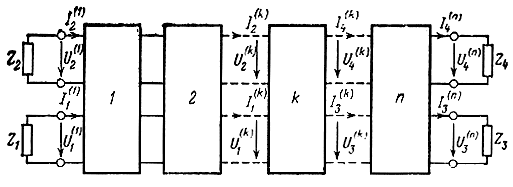
Рис. 2.2. Структурная схема однородного каскада УРУ

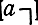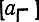Схема секции симметрична относительно вертикальной оси и может быть представлена в виде каскадного соединения двух взаимно обратных восьми полюсников: левого и правого, характеризуемых матрицами параметров соответственно и . Матрица Α-параметров секции, таким образом, представляет собой матричное произведение

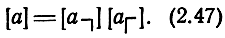
Пусть в какой-либо k-й секции в сечении по оси симметрии действуют независимые источники напряжения и тока (рис. 2.3). На рис. 2.3 элементы схемы замещения УЭ отнесены к левой и правой частям секции, а независимые источники образуют автономный восьми полюсник обозначенный пунктирной линией. Будем полагать, что в остальных секциях независимые источники отсутствуют.

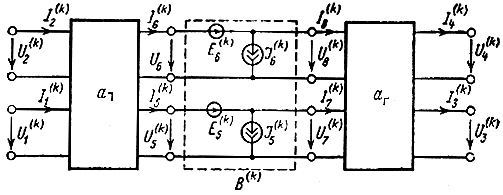
Рис. 2.3. Независимые источники в k-й секции

Записывая уравнения для k-x полусекций в СК χ

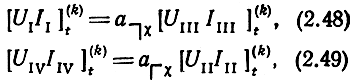
где

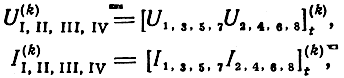
составляя уравнения для восьми полюсника B^(k)

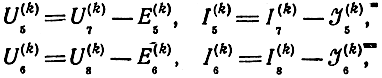
или в матричной форме

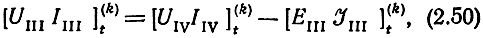
где

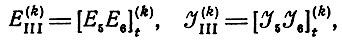
и подставляя (2.50) в (2.48), а (2.49) в (2.50), получим матричное уравнение для k-й секции

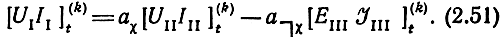
Поскольку уравнения частей каскада до k-й секции и после нее записываются в виде

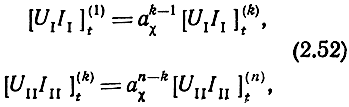
то можно связать входные и выходные напряжения и токи каскада, подставив (2.52) в (2.51)

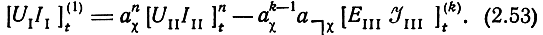
В уравнении (2.53)

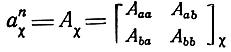
- матрица Α-параметров не автономного каскада УРУ,

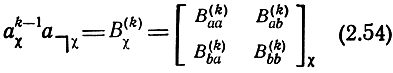
- матрица, определяющая наличие автономного восьми полюсника B^(k).

Записывая уравнение (2.53) в блочной форме

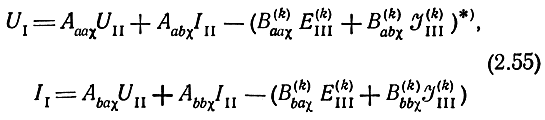
^* (Индексы (1) и (п) в (2.55) и далее опущены)

совместно с граничными уравнениями на концах каскада

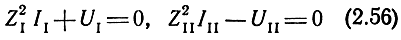
и решая (2.55) и (2.56) совместно относительно U₁₁ найдем

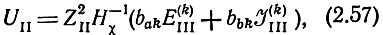
где матрица H_χ определяется по формуле (2.36), а

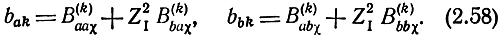
Из (2.57 ) может быть найдено напряжение на выходе каскада (U₄) как функция независимых источников, действующих в k-й секции, и параметров каскада. Подставляя в (2.57) формулы (2.58) и производя соответствующие операции над матрицами, определим напряжение U₄

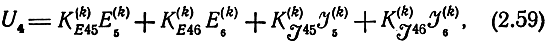
где

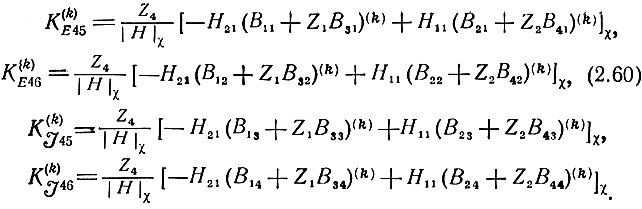
Все величины, входящие в выражения (2.59), (2.60), либо не нормированы, либо нормированы относительно произвольных сопротивлений. Нетрудно показать, что если нормирование входящих в (2.59) величин произведено относительно нагрузочных сопротивлений: U₄ относительно Z₄, E_5,6 и J_5,6 относительно Z_3,4, а матрица Α-параметров каскада и, следовательно, матрица B^(k) относительно Z_1,2 слева и Z_3,4 справа, то в (2.60) Z_i надлежит взять равными единице.