Глава 3. Матрицы секции и каскада усилителя с распределенным усилением

3.1. Матрицы Α-параметров секции УРУ с различными структурами

Секция является основой каскада УРУ. Схема секции (рис. 3.1) симметрична относительно вертикальной оси xx и состоит из трех частей: двух пассивных взаимно обратных частей (I, III) и усилительного элемента в восьми полюсном включении (II). I, III содержат по два не связанных между собой четырехполюсника, обладающих характеристическими сопротивлениями w_{1, 2H} с наружной стороны, w_{1, 2B} - с внутренней и постоянными распространения γ_1,2/2=α_1,2/2 + jβ_1,2/2. Индексы 1,2 характеризуют параметры соответственно входной и выходной линий.

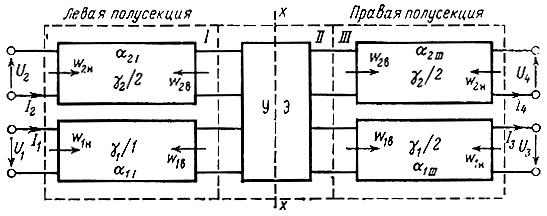
Рис. 3.1. Структурная схема секции

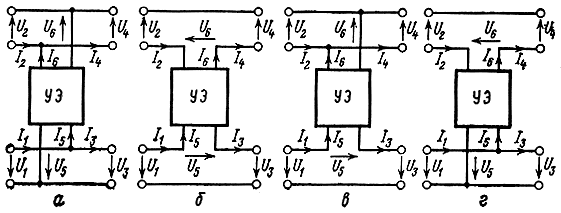
Рис. 3.2. УЭ в различных схемах включения в передающие линии: а) параллельной; б) последовательной; в) последовательно-параллельной; г) параллельно-последовательной

Усилительный элемент в различных схемах включения представлен на рис. 3.2 (34]. Под УЭ здесь понимается совокупность активного элемента и пассивных устройств, обеспечивающих последовательное включение активного элемента в передающие линии. Активный элемент может состоять из одного или нескольких транзисторов или электронных ламп. Схемы секции с различным включением УЗ, как указывалось ранее, будем называть структурами y, z, h, g.

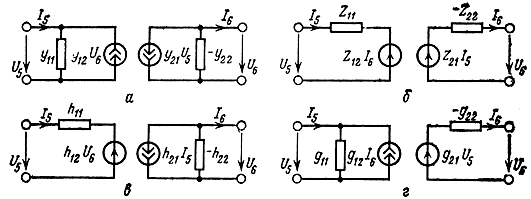
Рис. 3.3. Схемы замещения УЭ, соответствующие различным системам уравнений: а) в (y-параметрах; б) в z-параметрах; в) в h-параметрах; г) в g-параметрах

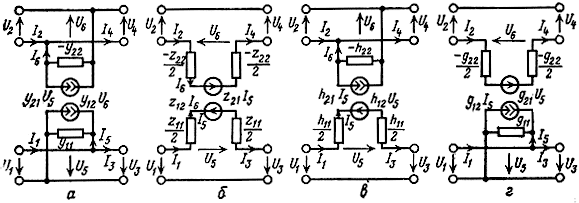
Рис. 3.4. Схемы замещения УЭ в восьми полюсном включении: а) ларалельном; 6) последовательном; в) последовательно-параллельном; г) параллельно-последовательном

В каждой из структур усилительный элемент удобно характеризовать следующими системами уравнений:

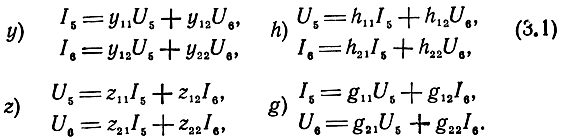
Уравнениям (3.1) соответствуют схемы замещения УЭ, показанные на рис. 3.3. Схемы замещения УЭ в восьми-полюсном включении представлены на рис. 3.4. Учитывая дополнительные связи между напряжениями и токами (рис. 3.2 и 3.4)

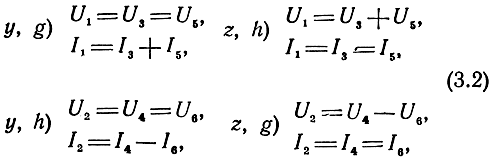
и решая (3.1) совместно с (3.2) для каждой структуры относительно внешних токов и напряжений, получим уравнения восьми полюсника II (рис. 3.1) в матричной записи в СК π

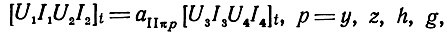
где

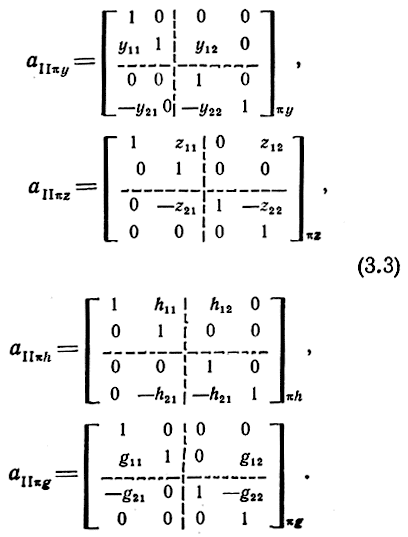
Если матрицы a_11πz, a_11πh, a_11πg представить в СК соответственно ξ, μ, ε (2.28), то матрицы (3.3) примут одинаковый вид

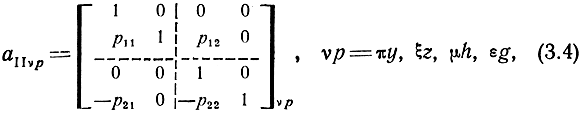
где

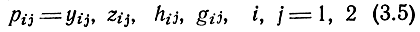
- обобщенные параметры УЭ.

Матрицы Л-параметров частей секции I, III записываются в виде

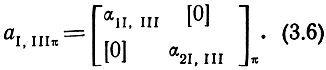
Нулевые матрицы в (3.6) означают отсутствие связи между пассивными четырехполюсниками передающих линий, описываемыми матрицами Α-параметров α_1,2I, и α_1,2III. Если учесть взаимную обратность частей I и III (вертикальная симметрия) и взять за основу Α-параметры четырехполюсников левой части секции

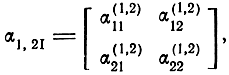
то α_1,2III будут связаны с α_1,2I следующим соотношением:

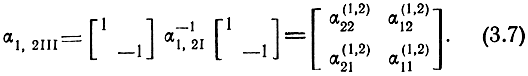
Матрицы α_1,2I и α_1,2III могут быть выражены через характеристические параметры соответствующих четырехполюсников (см. рис. 3.1)

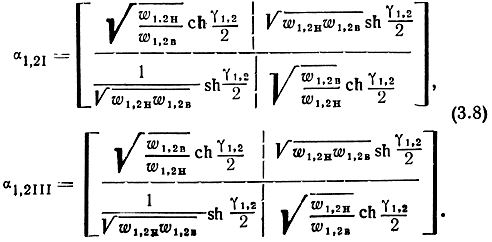
Матрицы Α-параметров всей секции различных структур находятся последовательным перемножением матриц восьми полюсников I, II, III, представленных в одинаковых С К.

Можно унифицировать матрицы Л-параметров секции всех структур, если, во-первых, принять, что сопротивления и проводимости с индексами 11 и 22 (±p_11,22) в схемах замещения (рис. 3.4) отнесены к четырехполюсникам передающих линий I, III (по половине к правым и левым четырехполюсникам) и учтены в их характеристических параметрах, а во-вторых, пронормировать напряжения и токи относительно w_H1,2 на внешних полюсах секции и относительно w_B1,2 в сечении слева и справа от усилительного элемента. В соответствии с первым условием в матрице (3.3) p_11,22 необходимо положить равными нулю. Нормирование видоизменяет параметры p_12,21 в матрице (3.3):

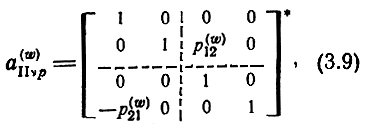
где p^(w)_12,21 определяются соотношениями

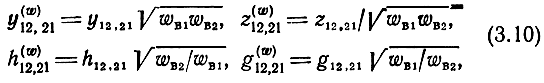
и упрощает матрицы частей I и III

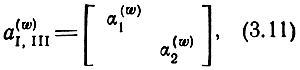
где

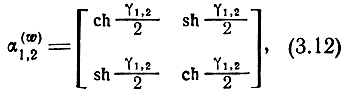
делая их одинаковыми и независимыми от систем координат π, ξ, μ, ε. Действительно, согласно (2.28) диагональная перестановка элементов внутри блоков α^(w)_1,2 изменяет их вида.

^* (Индексом (w) обозначаются величины, нормированные относительно характеристических сопротивлений.)

Матрицы нормированных Α-параметров секции всех структур в соответствующих системах координат находятся путем перемножения (3.11) и (3.9):

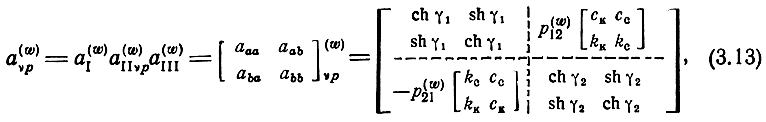
где

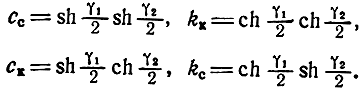
Таким образом, матрица (3.13) является унифицированной, характеризующей секцию одновременно всех структур. Однако необходимо помнить, что для каждой структуры матрица секции представлена в собственных системах координат (πy, ξz, μh, εg) и нормирована относительно характеристических сопротивлений четырехполюсников передающих линий.

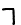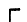В дальнейшем потребуются матрицы Α-параметров полусекций. Полусекция представляет собой левую или правую часть секции, расчлененной по оси симметрии хх (рис. 3.1). Левую и правую полусекции будем обозначать индексами соответственно "" и "". При разделении схемы восьми полюсника II по оси симметрии получаем два одинаковых восьми полюсника; при этом зависимые источники в схемах замещения (рис. 3.4) делятся пополам.

При этом

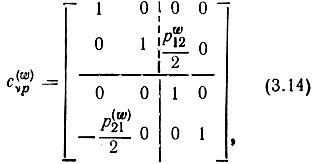
где с^(w)_νp - матрица Α-параметров разделенного восьми полюсника II.

Так как нормированные матрицы а_x и а_ш от структуры и систем координат не зависят, можно записать одновременно для всех структур в соответствующих СК

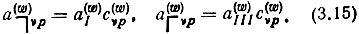
Подставив в (3.15) матрицы (3.11) и (3.14), получим

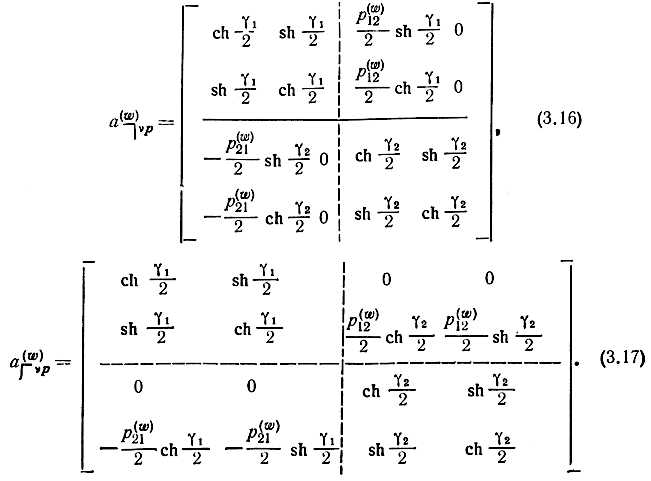
Матрица (3.16) нормирована слева относительно w_н1,2, справа относительно w_в1,2 в (3.17) обратное нормирование.