
3.2. Диагонализация матрицы секции и определение матриц Α-параметров каскада УРУ с различными структурами
Поставим задачу определения матрицы Α-параметров каскада УРУ, состоящего из цепочечного соединения одинаковых секций. Для этого необходимо матрицу a(w)νp секции возвести в n-ю степень
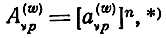
* (В процессе вывода матрицы Α-параметров каскада индексы (w), ν, р опускаются.)
где Α(w)νp - нормированная матрица Α-параметров каскада УРУ всех структур в соответствующих системах координат аналогично n-число секций в каскаде.
Для возведения а в n-ю степень необходимо провести ее диагонализацию, т. е. представить в виде [31]
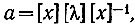
где [λ] - диагональная матрица, [x] - диагонализирующая матрица.
Тогда возведение в степень легко осуществить по формуле
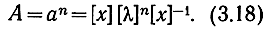
Элементами диагональной матрицы являются собственные числа характеристического уравнения, полученного из характеристической матрицы
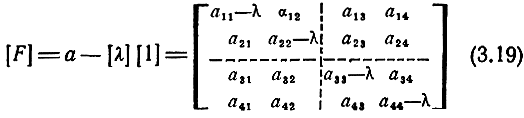
путем приравнивания нулю ее определителя. Раскрывая определитель матрицы (3.19) и подставляя элементы матрицы (3.13), получим
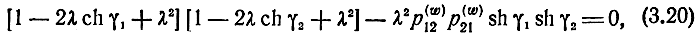
откуда найдем характеристическое уравнение в виде возвратного уравнения четвертой степени
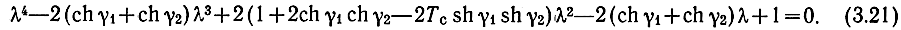
Здесь
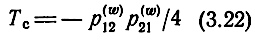
представляет собой возвратное отношение одной секции [2, 3] при характеристическом согласовании четырехполюсников передающих линий.
Уравнение (3.21) имеет следующие решения
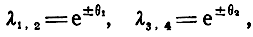
где
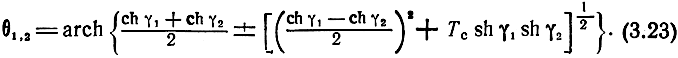
При отсутствии обратной связи (р(w)12 = 0) возвратное
отношение Tс равно нулю, а θ1,2 равны γ1,2, θ1,2 характеризуют распространение сигнала вдоль передающих линий в секции с учетом их взаимного влияния. Из (3.23) вытекают следующие соотношения
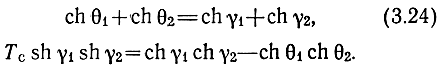
При γ1 = γ2, что обычно стремятся выполнить, и при малой обратной связи (|Tс|<<1) θ1,2 близки к γ1,2. Однако при цепочечном соединении секций nθ1,2 могут существенно отличаться от nγ1,2 даже при малой обратной связи.
Таким образом, диагональная матрица определена, а ее запись в блочной форме имеет вид
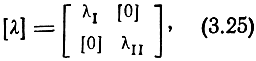
где
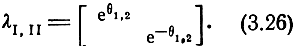
Диагонализирующую матрицу составим из первого столбца матрицы, взаимной по отношению к [F(λ)], подставляя в элементы каждого столбца соответствующие собственные числа λi, (i = 1-4). Как известно [31], элементами взаимной матрицы являются транспонированные алгебраические дополнения элементов исходной матрицы. Таким образом, диагонализирующая матрица может быть представлена в виде
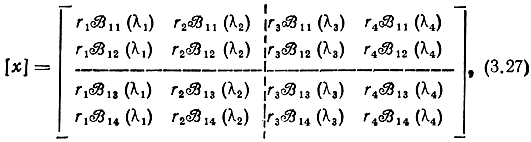
где 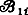 - алгебраические дополнения к [F(λ)], ri-произвольные коэффициенты.
- алгебраические дополнения к [F(λ)], ri-произвольные коэффициенты.
Алгебраические дополнения элементов первой строки матрицы (3.19)
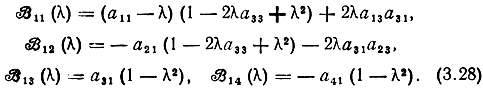
Можно показать, что подстановка в (3.28) элементов матрицы a, элементов диагональной матрицы и соотношений (3.24) приводит к более удобным выражениям для
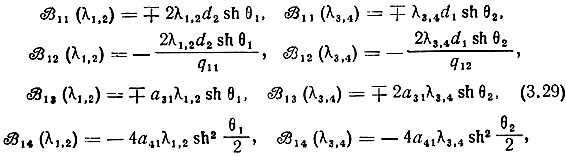
где
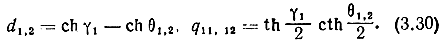
Приравнивая единице x11,12,43,44, избавимся от неопределенности произвольных коэффициентов ri
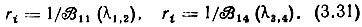
Подставляя (3.29) - (3.31) в (3.27), получим диагонализирующую матрицу в окончательном виде:
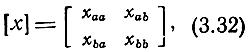
где
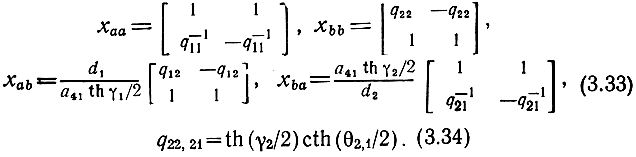
Матрица, обратная диагонализирующей, находится согласно общему правилу обращения блочной матрицы. В результате получим
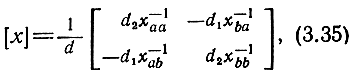
где
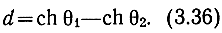
Итак, диагональная и диагонализирующие матрицы найдены. Матрица Α-параметров каскада определяется по формуле (3.18) путем подстановки в нее блочных матриц (3.25), (3.32), (3.35):
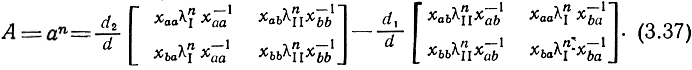
Используя (3.26) и (3.33), окончательно получим
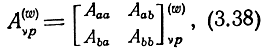
где
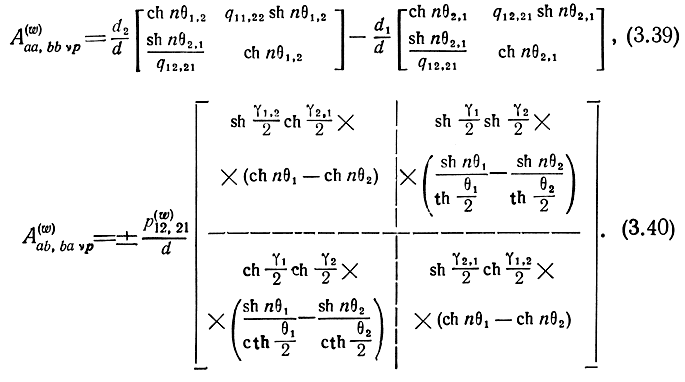
Матрицы (3.38) - (3.40) являются основой для определения волновых матриц передачи и рабочих коэффициентов передачи каскада УРУ различных структур. Полученными матрицами можно характеризовать и другие устройства, аналогичные по схеме каскаду УРУ. При этом, если четырехполюсники в средней части секции (рис. 3.2) пассивны, то в матрицах необходимо положить
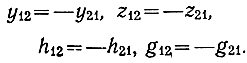

© RATELI.RU, 2010-2020
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
При использовании материалов сайта активной гиперссылки обязательна:
http://rateli.ru/ 'Радиотехника'
