4.2. Фильтр как линейный обратимый четырехполюсник

В связи со сложностью схем УРУ они должны анализироваться как с помощью приближенных соотношений, так и с помощью точных расчетов на ЭЦВМ. Приближенный анализ позволяет дать методику инженерного расчета УРУ. Применение ЭЦВМ дает возможность сравнить результаты более точных и приближенных расчетов. Кроме того, алгоритм матричных преобразований, изложенный в гл. 2, в дальнейшем станет основой машинного оптимального структурного синтеза УРУ. Поэтому нам требуются не только выражения для характеристических параметров фильтров, приводимые в литературе, как правило, для случая без потерь, но также и матрицы фильтров с учетом всех необходимых элементов, которые могут быть заложены в программу расчетов на ЭЦВМ.

Воспользуемся теорией четырехполюсников и фильтров [29, 35]. Полузвено фильтра представляет собой обратимый несимметричный четырехполюсник (рис. 4.3,а), описываемый системой уравнений:

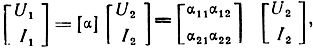
где через α_ij обозначены Α-параметры полузвена. Определитель матрицы [α] обратимого четырехполюсника равен единице. Матрица Α-параметров [α'] того же фильтра со стороны полюсов 2 может быть найдена из [α], если поменять местами ац и агг

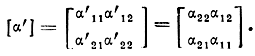
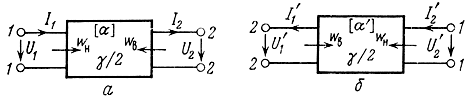
Рис. 4.3. Определение характеристических Параметров четырехполюсника

Характеристические параметры полузвена фильтра, необходимые для анализа УРУ, могут быть найдены по формулам

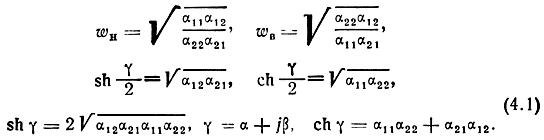
Для фильтров на сосредоточенных элементах (рис. 4.2) матрица Α-параметров и характеристические параметры имеют вид

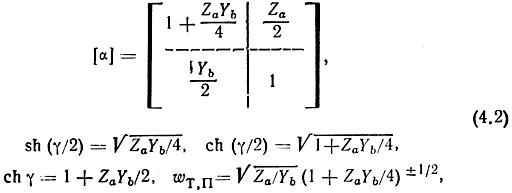
где w_Т,П обозначены характеристические сопротивления полузвена соответственно с Т- и П-образных сторон. При параллельном включении УЭ внутреннее характеристическое сопротивление звена w₀ = w_П, а наружное w_H = w_Т. При последовательном включении УЭ - наоборот: внутренним характеристическим сопротивлением является w_T а наружным - w_П.

Полузвено дискретно-распределенного фильтра (рис. 4.4) представляет собой каскадное соединение симметричного реактивного четырехполюсника с распределенными параметрами (ЧРП) и сосредоточенной комплексной проводимости Y_b/2. ЧРП состоит из распределенных по длине индуктивностей и емкостей (рис. 4.5) и характеризуется волновым сопротивлением ρ_k и фазовой постоянной g/2. Матрицы ЧРП и всего полузвена имеют вид

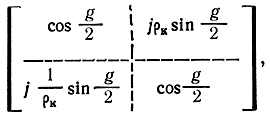
где

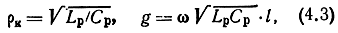
L_ρ, С_ρ - распределенные по длине в ЧРП погонные индуктивности и емкости;

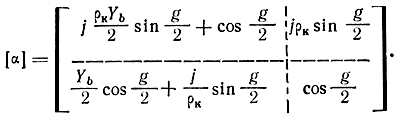_(4.4)

Из матрицы (4.4) по формулам (4.1) определяются характеристические параметры полузвена

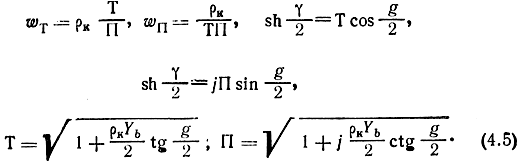
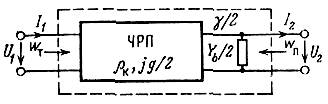
Рис. 4.4. Схема полузвена дискретно-распределенного фильтра

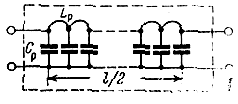
Рис. 4.5. Четырехполюсник с распределенными параметрами