4.6. Матрицы и формулы для расчета характеристик каскада УРУ на ЭЦВМ

Метод многополюсника оказывается весьма эффективным при расчете на ЭЦВМ характеристик каскада УРУ. При этом в основу программы расчета ложатся нормированные матрицы Α-параметров составных частей секции, а также алгоритм перемножения матриц и вычисления элементов матрицы рассеяния, представляющих собой нормированные рабочие коэффициенты передачи. Все величины нормируются относительно характерных сопротивлений: w₀ для ФНЧ k и ПТФ, ρ_k для ДРФ. Параметрам входной линии присваивается индекс 1, а параметрам выходной - индекс 2. Связь между параметрами входной и выходной линий вводится с помощью соответствующих коэффициентов.

Матрицы секции и каскада всех структур определяются в СК π, как наиболее удобной для записи матриц в блочной форме. После нахождения элементов матрицы каскада осуществляется перевод в СК χ. Матрицы полузвеньев фильтров с Т-образной стороны входной и выходной линий, нормированные относительно w_01,2 или ρ_k1,2, имеют вид:

для ПТФ и ФНЧ типа k, как частного случая от первого при q _п1,2 = 0 (4.16)

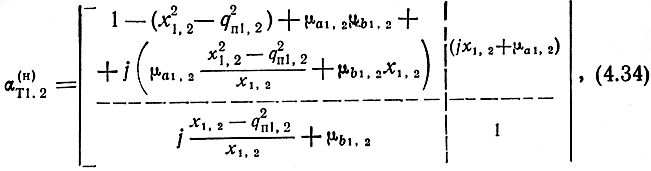
для ДРФ (4.24)

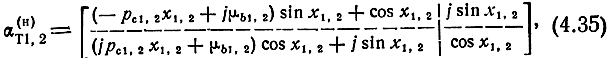
где индекс "н" означает операцию нормирования. В дальнейшем этот индекс для матриц а опустим. В (4.34)

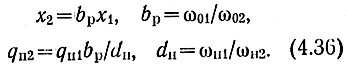
В (4.35)

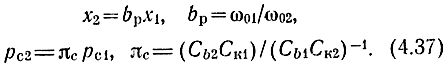
Для обеспечения синфазности в каскаде УРУ необходимо, чтобы коэффициенты b_p, d_H, π_с были равны единице. Однако при наличии потерь оптимальными могут оказаться значения, несколько отличающиеся от единицы.

Матрицы полузвеньев, определенные с П-образной стороны "α_П1,2" как уже указывалось образуются из α_T1,2 путем взаимной перестановки элементов, расположенных по главной диагонали. В матричной форме указанная перестановка записывается в виде

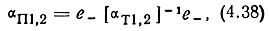
где

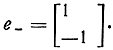
Рассмотрим случай, когда при параллельном включении УЭ в передающие линии секция оканчивается Т-образными концами, а при последовательном - П-образными. Тогда матрицы левого восьми полюсника секции (рис. 3.1) для различных структур можно представить в форме

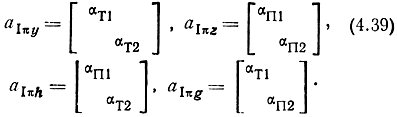
Для правого восьми полюсника секции имеем

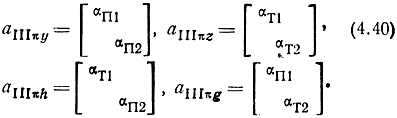
Используя (4.38), выразим (4.39), (4.40) через матрицы, являющиеся опорными

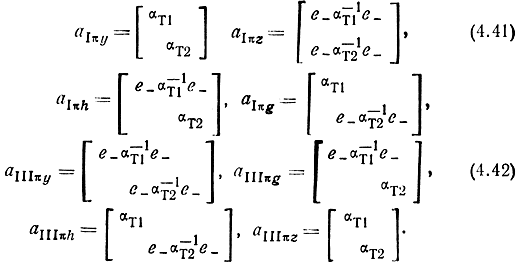
Как видно из (4.41), (4.42),

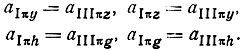
Матрицу с СК π левой или правой частей восьми полюсника II (рис. 3.1), разделенного по оси симметрии, найдем из (3.14) с использованием (2.25)

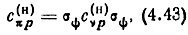
где σ_π = 1, σ_{ξ, μ, ε} определяйся по формулам (2.26)

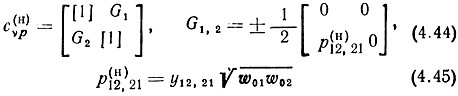
или

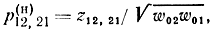
или

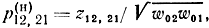
или

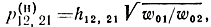
При использовании ДРФ в (4.45) w_01,2 необходимо заменить на ρ_к1,2.

Таким образом, имеем возможность, используя (4.41) - (4.43), определить матрицы полусекций и секций

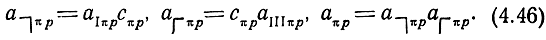
Матрица каскада находится последовательным перемножением

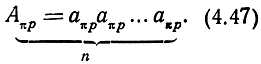
Далее используется алгоритм (2.32) для υ = π, ρ_1,3 = w₀₁ или ρ_k1, ρ_2,4 = w₀₂, или ρ_к2, Z_i = R_i и через (2.18) и (2.31) находятся нормированные рабочие коэффициенты передачи. В ненормированном виде они определяются с помощью соотношения

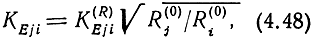
где R⁽⁰⁾_j,i = R_j,i/R₀ (R₀ - некоторое опорное сопротивление, равное, например, 75 Ом).

По изложенной методике производился расчет рабочих коэффициентов передачи и КСВН каскада структуры у на ФНЧ типа k и усилительных элементах, имеющих схему замещения триода с общим катодом, для которого нормированные параметры прямой и обратной передачи имеют вид

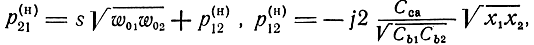
где s - крутизна триода; С_са - проходная емкость ка - анод. Исходными брались относительные величины:

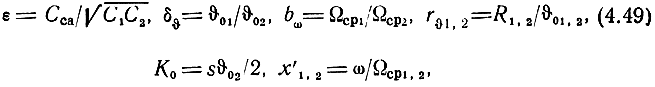
где

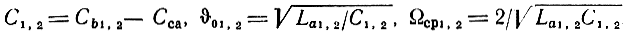
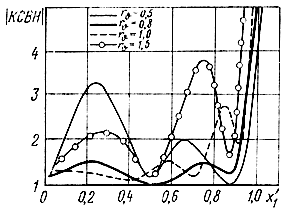
Рис. 4.14. Расчет КСВН передающей линии при n = 3, ε = 0, b_w = 1 и различных нагрузочных сопротивлениях

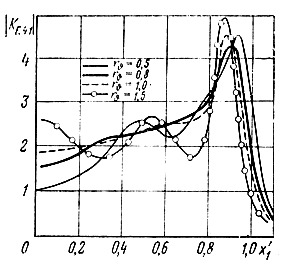
Рис. 4.15. Расчет АЧХ каскада при n = 3, ε = 0, b_w = 1 различных нагрузочных сопротивлениях

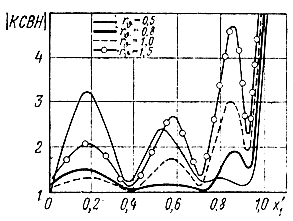
Рис. 4.16. Расчет КСВН передающей линии при n = 4, ε = 0, b_w =1 и различных нагрузочных сопротивлениях

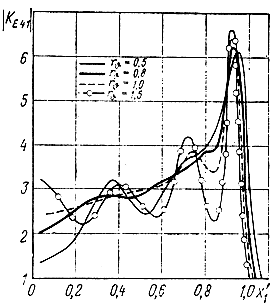
Рис. 4.17. Расчет АЧХ каскада при n = 4, ε = 0, b_w =1 и различных нагрузочных сопротивлениях

Аргументом являлась относительная текущая частота x'₁. Остальные величины (4.49) выполняли роль параметров (из них

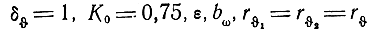
варьировались). Для сопоставления результатов расчета и эксперимента были учтены потери во входной и выходной линиях: μ_b1 =0,0375, μ_b2 = 0,02. При необходимости μ_b1,2 принимались равными нулю. Каскад был симметрично нагружен.

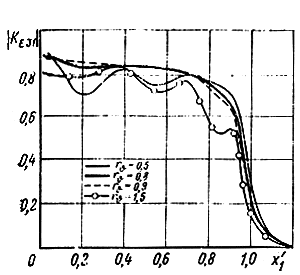
Рис. 4.18. Расчет модуля рабочего коэффициента передачи входной линии при n = 4, ε = 0, b_w = 1 и различных нагрузочных сопротивлениях

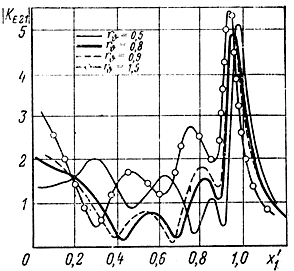
Рис. 4.19. Расчет модуля рабочего коэффициента передачи в сторону балластного нагрузочного сопротивления выходной линии при n = 4, δ = 0, b_w = 1

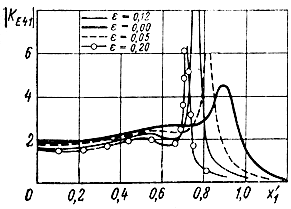
Рис. 4.20. Расчет АЧХ каскада при n = 3, r_θ = 1, b_w = 1 и различных значениях проходной емкости

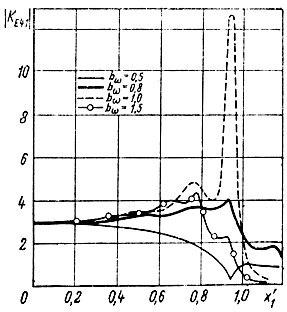
Рис. 4.21. Расчет АЧХ каскада при n = 4, ε = 0, r_θ = 1 и различном соотношении частот среза входной и выходной ПЛ

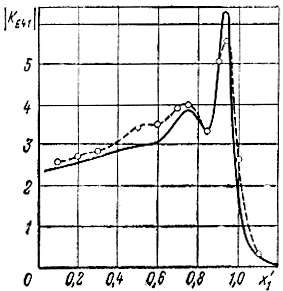
Рис. 4.22. Расчетная (_____) и экспериментальная (----) АЧХ каскада при n = 4, ε = 0, r_θ = 1, b_w = 1

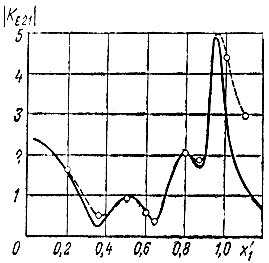
Рис. 4.23. Расчетная (_____) и экспериментальная (----) зависимость от частоты модуля рабочего коэффициента передачи каскада в сторону балластной нагрузки выходной линии при n = 4, ε = 0, r_θ = 1, b_w = 1

Некоторые из рассчитанных характеристик показаны на рис. 4.14-4.23. Следует отметить достаточно хорошее совпадение результатов расчета и эксперимента (рис. 4.22, 4.23).